
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пространства со скалярным произведением ⇐ ПредыдущаяСтр 7 из 7
Пусть F — одно из полей ℝ и ℂ, а V — векторное пространство над F. Отображение V × V → F, результат применения которого к паре векторов x, y ∈ V - xy (или (x, y), или 〈x | y〉) - скалярным произведением в V, если выполнены следующие аксиомы: 1) ∀x, y ∈ V xy = 2) ∀x, y ∈ V ∀α ∈ F (αx)y = α(xy); 3) ∀x, y, z ∈ V (x + y)z = xz + yz (скалярное произведение дистрибутивно относительно сложения векторов); 4) ∀x ∈ V xx ≥ 0, причем xx = 0 тогда и только тогда, когда x = 0.
Евклидовое пространство - пространство со скалярным произведением над ℝ. Унитарное пространство - пространство со скалярным произведением над ℂ.
Скалярный квадрат вектора х - скалярное произведение вектора на себя - Длина вектора x - это неотрицательное действительное число |x|:=
Угол между ненулевыми векторами x и y евклидова пространства - наименьший угол ϕ такой, что cos Угол между нулевым вектором и любым другим вектором не определен.
Расстояние между векторами x и y в пространстве со скалярным произведением - длина вектора x − y.
------------Ортогональность------------
Вектора x и y из пространства со скалярным произведением называются ортогональными, если xy = 0 - x ⊥ y. Набор векторов называется ортогональным, если любые два различных вектора из этого набора ортогональны.
Ортогональный набор векторов называется ортонормированным, если длины всех векторов из этого набора равны 1.
Ортогональный [ортонормированный] базис - ортогональный [ортонормированный] набор векторов, который является базисом.
Пусть S — подпространство в V. Ортогональное дополнение подпространства S - множество всех векторов, ортогональных к произвольному вектору из S -
Алгоритм нахождения базиса ортогонального дополнения:
● пусть a1, a2,..., ak — базис подпространства S евклидова пространства V. Составим однородную систему линейных уравнений
a11x1 + a12x2 +... + a1nxn = 0 a21x1 + a22x2 +... + a2nxn = 0 … ak1x1 + ak2x2 +... + aknxn = 0
в которой (ai1,..., aij) — это координаты вектора ai в некотором ортонормированном базисе пространства V. Фундаментальная система решений системы будет базисом подпространства
Пусть V — пространство со скалярным произведением, S — его подпространство и x ∈ V. В силу теоремы об ортогональном разложении существуют, и притом единственные, вектора y и z такие, что y ∈ S, z ∈ Вектор y называется ортогональной проекцией вектора x на подпространство S - xS. Вектор z называется ортогональной составляющей x относительно S - Расстояние от x до S - длина ортогональной составляющей вектора x относительно S - d(x, S).
Предположим теперь, что V — евклидово пространство. Угол между x и S - угол между векторами x и y, если S ≠ {0} и y ≠ 0 - Если S ≠ {0} и y = 0, то угол между x и S по определению считается равным Если S = {0}, то угол между x и S не определен.
Метод наименьших квадратов
Псевдорешение системы линейных уравнений Ax = b — это вектор x0, минимизирующий расстояние между векторами Ax и b. Если псевдорешение неединственно, то обычно интересуются псевдорешением наименьшей длины - нормальное псевдорешение. Метод наименьших квадратов - простое соображение, которое позволяет находить псевдорешения без вычисления ортогональной проекции.
-----Линейные функционалы-----
Пусть V — векторное пространство над произвольным полем F. Линейный функционал на V — это линейное отображение
Строение линейного функционала: Ker(Φ) — подпространство размерности dim V − 1, а его ортогональное дополнение
Фиксируем ненулевой вектор b ∈ Положим a:=
Φ(x) = Φ(c + γb) = Φ(c) + Φ(γb) = γΦ(b) = γβ, поскольку Φ(c) = 0. С другой стороны, xa = (c + γb) поскольку cb = 0.
---Сопряженное отображение---
Пусть В каждом из пространств V1 и V2 — свое скалярное произведение: будем обозначать произведение векторов x, y ∈ V1 через x Возьмем произвольный вектор r ∈ V2 и свяжем с ним отображение Φr: V1 → F, определенное правилом Φr(x):= Пусть пространство V1 конечномерно. По теореме о строении линейного функционала существует однозначно определяемый вектор a ∈ V1 такой, что
Ключевое тождество для сопряженного отображения:
или же, если вернутся к привычному обозначению
Преобразование Тождество самосопряженных преобразований:
Если Для матриц над ℝ свойство
Преобразование
Псевдообратное отображение
Пусть V = Ker Применяя ту же теорему к сопряженному отображению U = Ker Положим U0:= Im
Если A — матрица линейного отображения
Примеры задач
|
|||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 247; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.186.241 (0.045 с.) |
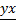 ;
;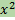 .
.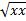 .
.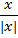 - орта вектора х - равна 1.
- орта вектора х - равна 1.
 .
.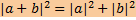 .
.
 для любых x, y ∈ V.
для любых x, y ∈ V.
 .
. — ортогональное дополнение S. Тогда:
1)
— ортогональное дополнение S. Тогда:
1) 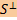 - ортогональным разложением пространства V относительно подпространства S.
- ортогональным разложением пространства V относительно подпространства S.
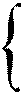
 = {0}, а
= {0}, а  = V;
2)
= V;
2) 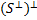 = S;
3) если S1 ⊆ S2, то
= S;
3) если S1 ⊆ S2, то 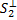 ⊆
⊆ 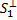 ;
4)
;
4) 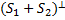 =
=  =
=  .
.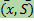 .
.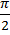 .
.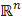 в пространство
в пространство 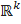 . Для произвольного вектора b ∈
. Для произвольного вектора b ∈ 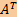 Ax =
Ax = 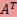 A.
A.
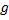 : V → F.
: V → F.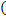 Ker(Φ)
Ker(Φ) 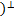 — одномерное подпространство в V.
— одномерное подпространство в V.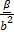 b и проверим, что Φ(x) = xa для каждого x ∈ V. Для этого представим x в виде x = c + γb для некоторого c ∈ Ker(Φ) и γ ∈ F. Такое представление возможно, так как V = Ker(Φ) ⊕
b и проверим, что Φ(x) = xa для каждого x ∈ V. Для этого представим x в виде x = c + γb для некоторого c ∈ Ker(Φ) и γ ∈ F. Такое представление возможно, так как V = Ker(Φ) ⊕ 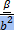 b = c
b = c 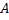 : V1 → V2 — линейное отображение (линейный оператор) пространств со скалярным произведением над полем F ∈ { ℝ, ℂ}.
: V1 → V2 — линейное отображение (линейный оператор) пространств со скалярным произведением над полем F ∈ { ℝ, ℂ}.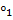 y, а произведение векторов p, q ∈ V2 — через p
y, а произведение векторов p, q ∈ V2 — через p 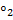 q.
q.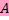 -
- 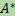 .
.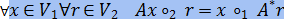
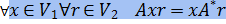
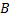 : V2 → V1 равенство
: V2 → V1 равенство 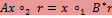 Br выполнено при всех x ∈ V1 и r ∈ V2, то
Br выполнено при всех x ∈ V1 и r ∈ V2, то 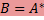 .
.
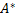 : V2 → V1 линейно.
: V2 → V1 линейно.
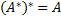 ;
2)
;
2) 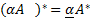 ;
3)
;
3) 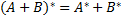 ;
4)
;
4) 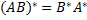 .
.
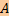 , то сопряженное ему отображение
, то сопряженное ему отображение 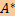 .
.
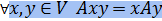
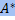 =
= 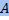 . Матрицы над ℂ со свойством
. Матрицы над ℂ со свойством 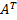 =
= 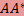 и
и 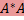 — самосопряженные преобразования.
— самосопряженные преобразования.
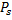 : V → V, сопоставляющее каждому вектору x ∈ V его ортогональную проекцию xS, называется ортогональным проектированием на S (ортопроектором).
: V → V, сопоставляющее каждому вектору x ∈ V его ортогональную проекцию xS, называется ортогональным проектированием на S (ортопроектором).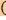 Im
Im 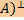 = Ker
= Ker 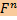 , либо сопряженная система
A ∗ y = 0 имеет нетривиальное решение y ∈
, либо сопряженная система
A ∗ y = 0 имеет нетривиальное решение y ∈ 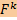 \ {0}.
\ {0}.
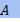 ⊕ Im
⊕ Im 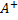 : V → U в тех же базисах называется псевдообратной к матрице A - A
: V → U в тех же базисах называется псевдообратной к матрице A - A 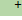 .
.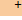 b возвращает ее нормальное псевдорешение.
Теорема Пенроуза:
Отображение
b возвращает ее нормальное псевдорешение.
Теорема Пенроуза:
Отображение 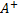 удовлетворяет следующим тождествам:
1)
удовлетворяет следующим тождествам:
1) 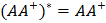 2)
2) 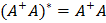 3)
3) 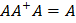 4)
4) 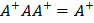 Обратно, если некоторое линейное отображение
Обратно, если некоторое линейное отображение 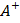 , то
, то 


