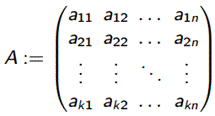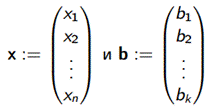Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обратимые линейные отображения и их матрицы. Ранг матрицыСодержание книги
Поиск на нашем сайте
Квадратная матрица А называется обратной к квадратной матрице В, если АВ = ВА = Е.
Ранг матрицы по столбцам - размерность подпространства, порожденного системой векторов-столбцов этой матрицы. Ранг матрицы по строкам - размерность подпространства, порожденного системой векторов-строк этой матрицы.
Элементарные преобразования: ● перестановка двух столбцов (строк); ● прибавление к столбцу (строке) другого столбца (другой строки); ● умножение столбца (строки) на ненулевой скаляр.
Если поменять ролями строки и столбцы матрицы
----------Применение ранга----------
Алгоритм вычисления ранга: ● с помощью элементарных преобразований над столбцами и строками матрицы привести ее к виду
где на местах 1,1; 2,2; …; r,r стоят 1, а на всех остальных местах стоят 0. Число r и будет рангом матрицы. Пример: ранг такой матрицы равен 2
Алгоритм вычисления обратной матрицы: ● припишем к обратимой n
● проделаем над строками n ● левая половина получившейся матрицы будет равна матрице
Пример:
Рассмотрим произвольную систему k линейных уравнений c n неизвестными:
a11x1 + a12x2 +... + a1nxn = b1 a21x1 + a22x2 +... + a2nxn = b2 … ak1x1 + ak2x2 +... + aknxn = bk
Эту систему можно кратко записать в виде Ax = b, если ввести обозначения:
- основная матрица системы.
- столбцы неизвестных и свободных членов.
Матрица размера k × (n + 1), получаемая приписыванием к основной матрице системы столбца свободных членов называется расширенной матрицей системы.
Системы линейных уравнений
Система линейных уравнений называется однородной, если свободные члены всех уравнений системы нулевые:
a11x1 + a12x2 +... + a1nxn = 0 a21x1 + a22x2 +... + a2nxn = 0 … ak1x1 + ak2x2 +... + aknxn = 0
Фундаментальная системой решений - любой базис пространства, если пространство решений однородной системы ненулевое.
b11y1 + b12y2 +... + b1ryr = - b1 r+1yr+1 -... - b1nyn b21y1 + b22y2 +... + b2ryr = - b2 r+1yr+1 -... - b2nyn … bk1y1 + bk2y2 +... + bkryr = - br r+1yr+1 -... - brnyn
Неизвестные yr+1,..., yn - свободные, а неизвестные y1,..., yr - связанные.
Процедура решения системы линейных уравнений: ● элементарными преобразованиями строк приводим матрицу A|b к ступенчатому виду; ● если ранг r матрицы A меньше ранга матрицы A|b, система Ax = b несовместна; если ранги равны, находим частное решение x0 этой системы;
● находим фундаментальную систему решений x1,..., xn−r соответствующей однородной системы Ax = 0; ● выражение x = x0 + c1x1 + c2x2 + · · · + cn−rxn−r, где c1, c2,..., cn−r — произвольные скаляры, дает общее решение системы Ax = b. Каждое решение системы получается из общего при некотором (однозначно определяемом) наборе c1, c2,..., cn−r. Тема 6: Евклидовы и унитарные пространства
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 334; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.240.72 (0.01 с.) |

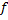 - линейное взаимно однозначное отображение векторного пространства V1 на векторное пространство V2, то обратное отображение
- линейное взаимно однозначное отображение векторного пространства V1 на векторное пространство V2, то обратное отображение 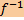 пространства V2 в V1 также является линейным и взаимно однозначным.
пространства V2 в V1 также является линейным и взаимно однозначным.
 обратима, если существует обратная к
обратима, если существует обратная к 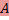 матрица
матрица 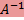 .
.
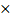 n обратима тогда и только тогда, когда ее ранг совпадает с n.
n обратима тогда и только тогда, когда ее ранг совпадает с n.
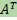 = (aji)n×k.
= (aji)n×k.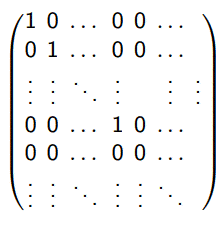 ,
,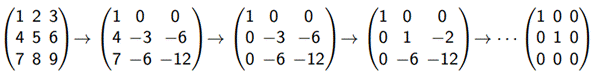
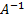 .
.