
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Система координат. Координаты точки
Система координат в пространстве [на плоскости] - совокупность базиса пространства [соответственно базиса плоскости] и точки [принадлежащей этой плоскости] - (О; Начало системы координат - точка, входящая в систему координат. Прямые, проходящие через точку O параллельно одному из базисных векторов, называются осями координат. Ось абсцисс - прямая, проходящая через точку O параллельно вектору Ось ординат - прямая, проходящая через точку O параллельно вектору Ось аппликат - прямая, проходящая через точку O параллельно вектору Координатные плоскости - плоскости, проходящие через точку O и две из трех осей координат.
Зафиксируем в пространстве некоторую систему координат (О; Радиус-вектор точки М - вектор Координаты точки M в системе координат (О; Координаты точки на плоскости определяются аналогично координатам точки в пространстве. Пусть точки A и B имеют координаты (a1, a2, a3) и (b1, b2, b3) соответственно. Тогда
|AB| =
Система координат в пространстве (О; Система координат на плоскости (O;
Предположим, что даны различные точки A и B и число t. Будем говорить, что точка C делит отрезок AB в отношении t, если
(
Тема 2: Прямые и плоскости --------Прямая на плоскости--------
Геометрический объект на плоскости (в пространстве) - произвольное множество точек плоскости (пространства), возможно, пустое.
Пусть π — плоскость, в которой зафиксирована система координат, а ℓ — некоторый геометрический объект в этой плоскости. Уравнение F(x, y) = 0, где F(x, y) — функция двух переменных, называется уравнением ℓ, если точка плоскости π принадлежит ℓ тогда и только тогда, когда ее координаты удовлетворяют этому уравнению - объект ℓ задается уравнением F(x, y) = 0 или ℓ является геометрическим образом этого уравнения.
Направляющий вектор прямой - любой ненулевой вектор, коллинеарный данной прямой.
- параметрические уравнения прямой на плоскости.
Пусть прямая ℓ задана уравнением Ax + By + C = 0. Тогда вектор
y = kx + b - уравнение прямой с угловым коэффициентом k.
Пусть ℓ — прямая, заданная уравнением Ax + By + C = 0. Вся плоскость делится этой прямой на три непересекающиеся части: саму прямую ℓ и две полуплоскости.
d(M, ℓ) = | Метод Крамера
Если определитель системы не равен 0, то рассматриваемая система имеет только одно решение, причем
-----------------Плоскость-----------------
Направляющий вектор плоскости - любой ненулевой вектор, коллинеарный данной плоскости.
x = x0 + q1u + q2v
y = y0 + r1u + r2v - параметрические уравнения плоскости.
z = z0 + s1u + s2v
Пусть плоскость π задана уравнением Ax + By + Cz + D = 0. Тогда вектор
Пусть плоскость σ задана уравнением Ax + By + Cz + D = 0. Все пространство делится этой плоскостью на три непересекающиеся части: саму плоскость σ и два полупространства.
d(M, σ) =
------Прямая в пространстве------
x = x0 + qt
y = y0 + rt - параметрические уравнения прямой в пространстве.
z = z0 + st
A1x + B1y + C1z + D1 = 0 - общие уравнения прямой в пространстве. A2x + B2y + C2z + D2 = 0
d(M, ℓ) =
Пусть ℓ1 и ℓ2 — скрещивающиеся прямые. Общим перпендикуляром к прямым ℓ1 и ℓ2 называется прямая, перпендикулярная к каждой из прямых ℓ1 и ℓ2 и пересекающая каждую из них.
Расстояние между скрещивающимися прямыми ℓ 1 и ℓ 2 - расстояние между точками, в которых общий перпендикуляр к скрещивающимся прямым ℓ1 и ℓ2 пересекает эти прямые. d(ℓ1, ℓ2) =
Если в пространстве заданы прямые с направляющими векторами (q1,r1,s1) и (q2,r2,s2), то угол α между этими прямыми: cos α = Если прямые на плоскости заданы уравнениями A1x + B1y + C1 = 0 и A2x + B2y + C2 = 0, то угол α между этими прямыми: cos α = Если плоскости заданы уравнениями A1x + B1y + C1z + D1 = 0 и A2x + B2y + C2z + D2 = 0, то угол между этими плоскостями можно найти, вычисляя угол α между их главными векторами: cos α = Если α — угол между ℓ и ℓ1, а β — острый угол между ℓ и ℓ2, то α + β = 90°. Пусть (q,r,s) — направляющий вектор прямой ℓ, а Ax + By + Cz + D = 0 — уравнение плоскости σ. Тогда прямая ℓ2 коллинеарна главному вектору (A, B, C) плоскости σ. Отсюда угол между прямой и плоскостью:
sin α = cos β = Тема 3: Комплексные числа -----------Формула Кардано-----------
x = u + v =
Поле - неодноэлементное ассоциативное и коммутативное кольцо с 1, в котором все ненулевые элементы обратимы. Поле комплексных чисел: ● содержит поле R действительных чисел; ● содержит квадратные корни из отрицательных чисел; ● не содержит ничего лишнего.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 143; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.181.231 (0.084 с.) |
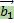 ,
, 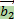 ,
,  ) или (О;
) или (О; 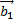 .
.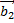 .
. .
. .
. = (b1 - a1, b2 - a2, b3 - a3)
= (b1 - a1, b2 - a2, b3 - a3)
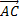 = t *
= t * 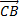 .
.

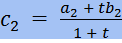 - формулы деления отрезка в отношении t.
- формулы деления отрезка в отношении t.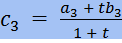
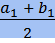 ,
, 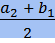 ,
, 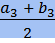 ) - координаты середины отрезка.
) - координаты середины отрезка.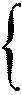

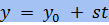
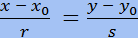 - каноническое уравнение прямой на плоскости.
- каноническое уравнение прямой на плоскости.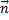 = (A,B) называется главным вектором прямой ℓ.
= (A,B) называется главным вектором прямой ℓ.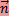 = (A, B) перпендикулярен этой прямой.
= (A, B) перпендикулярен этой прямой.
 - уравнение прямой на плоскости по 2 точкам.
- уравнение прямой на плоскости по 2 точкам.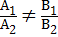 ;
2) параллельны тогда и только тогда, когда
;
2) параллельны тогда и только тогда, когда 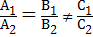 ;
3) совпадают тогда и только тогда, когда
;
3) совпадают тогда и только тогда, когда 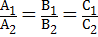 .
.


 | =
| = 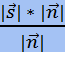 =
=  =
= 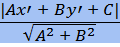 - расстояние от точки М до прямой ℓ.
- расстояние от точки М до прямой ℓ.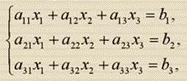
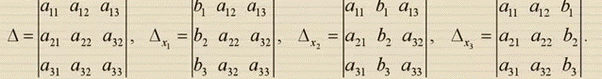
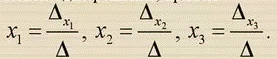
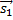 = (−B, A, 0),
= (−B, A, 0), 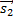 = (−C, 0, A) и
= (−C, 0, A) и 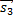 = (0, −C,B). Тогда по крайней мере два из векторов
= (0, −C,B). Тогда по крайней мере два из векторов 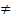 0, то этими свойствами обладают вектора
0, то этими свойствами обладают вектора 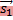 и
и 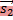 , если B
, если B 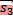 , а если C
, а если C 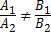 или
или 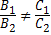 ;
2) параллельны тогда и только тогда, когда
;
2) параллельны тогда и только тогда, когда 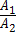 =
= 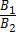 =
= 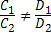 ;
3) совпадают тогда и только тогда, когда
;
3) совпадают тогда и только тогда, когда 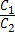 =
= 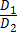 .
.
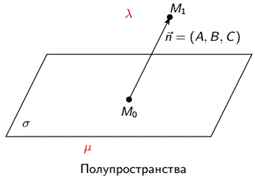
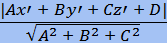 - расстояние от точки М до плоскости σ.
- расстояние от точки М до плоскости σ.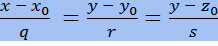 - канонические уравнения прямой в пространстве.
- канонические уравнения прямой в пространстве.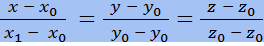 - уравнения прямой в пространстве по 2 точкам.
- уравнения прямой в пространстве по 2 точкам.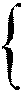
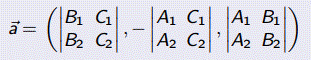 является направляющим вектором прямой, заданной общими уравнениями прямой в пространстве.
является направляющим вектором прямой, заданной общими уравнениями прямой в пространстве.
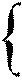 x = x0 + qt
y = y0 + rt
z = z0 + st
Тогда:
1) ℓ и σ пересекаются тогда и только тогда, когда Aq + Br + Cs
x = x0 + qt
y = y0 + rt
z = z0 + st
Тогда:
1) ℓ и σ пересекаются тогда и только тогда, когда Aq + Br + Cs 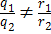 , либо
, либо 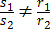 ;
;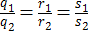 и либо
и либо 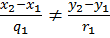 , либо
, либо 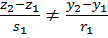 ;
;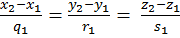 .
.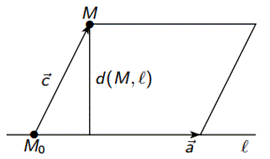
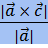 =
= 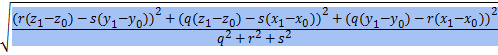 - расстояние от точки М до прямой ℓ.
- расстояние от точки М до прямой ℓ.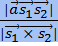
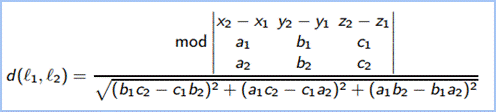
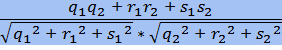
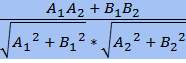
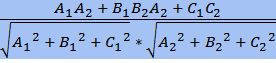
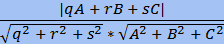
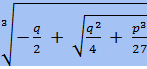 +
+ 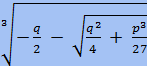 - формула Кардано (для уравнения вида
- формула Кардано (для уравнения вида 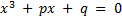 ).
).


