
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення моменту інерції системиСодержание книги
Поиск на нашем сайте
На прикладі маятника Обербека
Мета роботи: експериментально визначити момент інерції системи динамічним методом та порівняти отримані результати з теоретичними обчисленнями. Прилади та обладнання: маятник Обербека, міліметрова лінійка, секундомір.
Теоретичні відомості Обертальним рухом твердого тіла (системи) відносно нерухомої осі називається такий рух, під час якого всі точки тіла (системи) рухаються в площинах, перпендикулярних до осі обертання, і описують кола з центрами на цій осі.
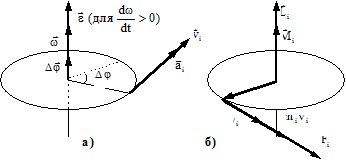
Рис. 1.
Кінематика та динаміка обертального руху характеризується відповідно кутом повороту s = jr, Динамічні характеристики обертального руху визначаються наступними виразами:
Взаємозв’язок між відповідними величинами додатково розкривається при графічному зображенні векторних величин, що розглядаються в лабораторній роботі (див. рис. 1: а – кінематика, б – динаміка). Основний закон динаміки обертального руху тіла відносно нерухомої осі обертання має наступний вигляд:
Для тіл правильної геометричної форми момент інерції простіше визначити аналітично, для тіл неправильної геометричної форми – експериментально. З експериментальних найбільш поширеними є методи, які основуються на використанні основного закону динаміки обертального руху, закону збереження та перетворення енергії та законів коливального руху.
Опис методу
У роботі використовується динамічний метод із застосуванням основного закону динаміки обертального руху. Маятник Обербека, момент інерції якого треба визначити, складається із закріпленого на горизонтальній осі шківа (рис. 2) з радіально розташованими стержнями, на яких симетрично закріплені чотири тягарці масами m1. На шків намотана нитка, один кінець якої закріплений до шківа, а на другому кінці підвішений тягарець масою m. Під час опускання тягарця m маятник Обербека під дією сили натягу нитки Основне рівняння динаміки обертального руху для маятника Обербека має вигляд: де r– радіус шківа. Моментом сили тертя нехтуємо. Напрямок вектора моменту
Прирівнявши праві частини рівнянь (1) та (2), отримаємо
звідки:
Робочу формулу для розрахунку моменту інерції J знайдемо, використавши величини h і t, які вимірюються в процесі експерименту, де h – шлях руху тягарця m по вертикалі, t – час його руху. Виразивши кутове прискорення e через лінійне прискорення точок a, які знаходяться на ободі шківа, зведемо задачу до знаходження лише a. Оскільки тягарець m рухається прямолінійно і рівноприскорено, то його шлях h, пройдений за час t, можна визначити за формулою:
Тоді кутове прискорення маятника: Підставивши значення a та e у рівняння (3), отримаємо:
Якщо врахувати можливі числові значення величин в нашому експерименті (h» 1 м, t» 10 c Þ gt2/2h» 500), то в формулі (4) можна знехтувати одиницею і отримати спрощений вираз: Формула (5) є робочою для експериментального визначення моменту інерції маятника Обербека. В роботі виконуються прямі вимірювання величин h і t, значення величин m, m1 та r наведені в паспорті установки.
Порядок виконання роботи
1. Перевірити роботу маятника Обербека, зробивши декілька пробних запусків установки. Звернути увагу на вільність обертання шківа та опускання тягарця масою m, а також на збалансованість маятника. При необхідності відрегулювати установку (можливо з допомогою лаборанта). 2. Вибрати певну довжину шляху h руху тягарця m, яка буде однаковою для всіх вимірів. 3. Намотати нитку на шків так, щоб нижня частина тягарця знаходилась на рівні початку відліку шляху (висоти) руху тягарця. Відпустити тягарець m і одночасно ввімкнути секундомір. Зробити 5 вимірів. Записати в таблицю 1 значення h і t. 4. Зняти всі чотири тягарці m1 і повторити експеримент для того ж самого шляху h. Результати вимірювання часу t' занести до таблиці 1. Обчислення середніх значень 1. Обчислити середнє значення часу t та t', моменту інерції маятника з тягарцями J і маятника без тягарців J' за робочою формулою (5). Для моделі абсолютно твердого тіла, яка використовується для розгляду обертального руху тіла, при обчисленні моментів інерції використовується адитивність (незалежне складання) моментів інерції всіх матеріальних точок тіла або, таким чином, будь-яких його частин. Тому момент інерції маятника Обербека J дорівнює сумі моментів інерції маятника без тягарців J' і моментів інерції самих тягарців J0е: J = J' + J0е, звідки експериментальне значення величини моменту інерції чотирьох тягарців J0е = J - J'. З іншого боку, якщо розглядати тягарці як матеріальні точки, то теоретичне значення їх моменту інерції J0т = 4m1R2 , де R – відстань від осі обертання до центру тяжіння тягарців масами m1.
Таблиця 1 Результати вимірювань та вихідні дані для розрахунків
h=.....; m=..... ±.....; m1=..... ±.....; r=..... ±.....; R=.....;
2. Обчислити теоретичне значення моменту інерції тягарців J0т та порівняти його з експериментальним.
Питання для самоперевірки 1. Навести формулу, що пов’язує швидкість поступального руху з кутовою швидкістю. 2. Що таке кутове прискорення? 3. Що таке момент сили, від чого він залежить і за яким правилом визначається напрямок вектора моменту сили? 4. Що таке момент імпульсу і від чого він залежить? 5. Дати визначення моменту інерції матеріальної точки і твердого тіла. 6. Від чого залежить момент інерції тіла? 7. Запишіть основне рівняння динаміки обертального руху тіла (загальний і окремий випадок). 8. Як зміниться момент інерції диска відносно вісі обертання, що проходить через його центр мас, якщо радіус диска збільшити у два рази? 9. Як зміниться момент інерції диска відносно вісі обертання, що проходить через його центр мас, якщо масу диска збільшити у два рази? 10. Швидше чи повільніше буде обертатися уся система, якщо тягарці на спицях маятника Обербека розмістити ближче до вісі обертання? Відповідь пояснити, використовуючи відповідні формули.
Лабораторна робота № 3
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-10; просмотров: 250; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.138.214 (0.008 с.) |

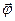 , приростом кута повороту
, приростом кута повороту 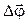 , кутовою швидкістю
, кутовою швидкістю 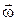 , кутовим прискоренням
, кутовим прискоренням 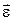 , моментом інерції J, моментом сили
, моментом інерції J, моментом сили 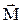 , моментом імпульсу
, моментом імпульсу 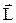 , які виконують таку саму роль для обертального руху, як і відповідні величини – шлях S, переміщення
, які виконують таку саму роль для обертального руху, як і відповідні величини – шлях S, переміщення 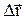 , швидкість
, швидкість 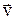 , прискорення
, прискорення 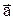 та маса m, сила
та маса m, сила 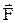 , імпульс
, імпульс 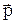 - для поступального руху. Зв’язок між лінійними і відповідними кутовими кінематичними величинами здійснюється через радіус обертання r (радіус-вектор
- для поступального руху. Зв’язок між лінійними і відповідними кутовими кінематичними величинами здійснюється через радіус обертання r (радіус-вектор 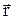 ) таким чином:
) таким чином: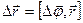 ,
, 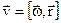 ,
, 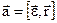 .
.
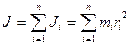 ,
, 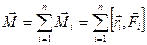 ,
,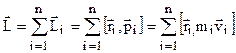 .
.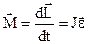 . (1)
. (1)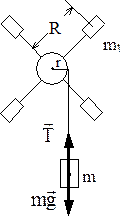
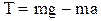 приводиться в рівноприскорений обертальний рух.
приводиться в рівноприскорений обертальний рух.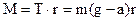 , (2)
, (2)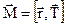 .
.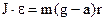 ,
,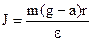 . (3)
. (3)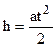 , звідки
, звідки 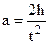 .
.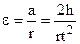 .
.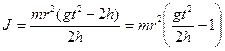 . (4)
. (4)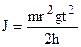 . (5)
. (5)


