Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Міністерство освіти і науки україни. Міністерство освіти і науки україниСодержание книги
Поиск на нашем сайте
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ НАЦІОНАЛЬНИЙ ТРАНСПОРТНИЙ УНІВЕРСИТЕТ МЕТОДИЧНІ ВКАЗІВКИ До виконання лабораторних робіт З використанням комп’ютерного експерименту з дисципліни „Концепції сучасного природознавства” для студентів спеціальності 8.050201 „Менеджмент організацій” В рамках кредитно–модульної системи Організації навчального процесу
ЗАТВЕРДЖЕНО на засіданні навчально–методичної Ради Національного транспортного університету Протокол №___від______________2007 р.
Київ НТУ 2007 Методичні вказівки до виконання лабораторних робіт з використанням комп’ютерного експерименту з дисципліни „Концепції сучасного природознавства” для студентів спеціальності 8.050201 „Менеджмент організацій” в рамках кредитно–модульної системи організації навчального процесу // Укл.: Гололобов Ю.П., Іщенко Р.М., Шатній Т.Д. – К.: НТУ, 2007. – 37 с.
Укладачі: Гололобов Ю.П. – доктор фіз.-мат. наук Іщенко Р.М. – кандидат фіз.-мат. наук Шатній Т.Д. – кандидат фіз.-мат. наук Відповідальний за випуск: Іщенко Р.М.
Вступ
На сучасному етапі розвитку суспільства бути кваліфікованим спеціалістом неможливо без знань основних концепцій сучасного природознавства. Формування наукового світогляду та наукового стилю мислення у значній мірі залежить від засвоєння найбільш важливих досягнень природознавства як сукупності наук про природу. Кожен студент, який в подальшому збирається стати менеджером, економістом чи юристом, щоб почувати себе високоосвіченою людиною, повинен знати що таке теорія відносності, квантова механіка, синергетика та інші науки. Навчальною програмою з дисципліни „Концепції сучасного природознавства” окрім лекційного курсу передбачено виконання студентами циклу лабораторних робіт. Такий підхід сприяє формуванню навичок щодо використання одержаних знань для розв’язку практичних задач, зокрема техніко-інженерного напрямку. Кредитно–модульна система організації навчального процесу, яка впроваджується в Національному транспортному університеті, передбачає використання як традиційних методів виконання лабораторних робіт (проведення фізичного експерименту), так і новітніх методів, зокрема, використання комп’ютерного експерименту. Тому в даних методичних вказівках до виконання лабораторних робіт з дисципліни „Концепції сучасного природознавства” для студентів спеціальності „Менеджмент організацій” разом з роботами, які виконуються безпосередньо при проведені фізичного експерименту, представлено лабораторну роботу „Моделювання криволінійного руху тіла”, що виконується з використанням комп’ютерного експерименту. Для покращення засвоєння навчального матеріалу в методичних вказівках після кожної лабораторної роботи наведено питання для самоперевірки знань студентів.
Лабораторна робота № 1 (з використанням комп’ютерного експерименту) Моделювання криволінійного руху тіла
Мета роботи: вивчити основні положення кінематики і динаміки матеріальної точки та закономірності руху тіл в однорідному полі тяжіння. Дослідити вплив опору повітря на форму траєкторії, дальність і висоту польоту.
Теоретичні відомості Нехай тіло масою m кинуто під кутом α до горизонту зі швидкістю v0. Знайдемо його траєкторію з врахуванням опору повітря і порівняємо її з траєкторію, отриманою при нехтуванні опором повітря. Вважаючи тіло матеріальною точкою, запишемо для нього другий закон Ньютона:
де g - прискорення вільного падіння, v = v (t) - швидкість тіла у довільній момент часу t,
де r – коефіцієнт опору (він залежить від розмірів і форми тіла та від властивостей середовища, в якому тіло рухається). Виберемо декартову систему координат так, щоб вектор початкової швидкості знаходився у площині Oxy, спрямуємо вісь Oy вертикально вгору перпендикулярно поверхні землі і позначимо через
або
Якщо у момент кидання t = 0 тіло знаходиться у точці з координатами х0, у0, то початкові умови задачі є такими:
при t = 0 x = x0, y = y0, де – проекції початкової швидкості на вісі координат. Розв’яжемо отримані диференціальні рівняння для двох випадків. 1. Опором повітря нехтуємо, r = 0. Запишемо для цього випадку рівняння (3а, 3b):
та інтегруємо їх з врахуванням початкових умов (5):
В результаті отримуємо відомі формули: vx = v0x, vy = v0y – gt, (7)
згідно з якими рух тіла у горизонтальному напрямку є рівномірним, а у вертикальному – рівноприскореним. Знайдемо траєкторію тіла у параметричному вигляді: х = х (t), у = у (t). Для цього врахуємо, що vx = dx/dt, vy = dy/dt, перепишемо рівняння (7) у вигляді:
dx = v0x·dt, dу = v0y·dt – gt·dt
і проінтегруємо їх з врахуванням початкових умов (5):
В результаті отримуємо траєкторію тіла: x(t) = x0 + v0xt, (8a) y(t) = y0 + v0yt –
2. Враховуємо силу опору повітря, r > 0. У цьому випадку інтегруємо рівняння (4а):
і знаходимо:
де β = r/m. (10)
Аналогічно, інтегруючи рівняння (4b):
знаходимо:
Зауважимо, що при Для знаходження траєкторії тіла у параметричному вигляді інтегруємо з врахуванням початкових умов (5) рівняння (9) і (11):
В результаті знаходимо траєкторію тіла з врахуванням сили опору повітря:
Приклад
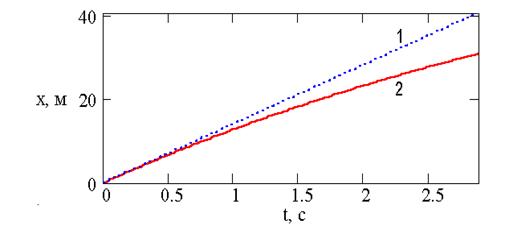
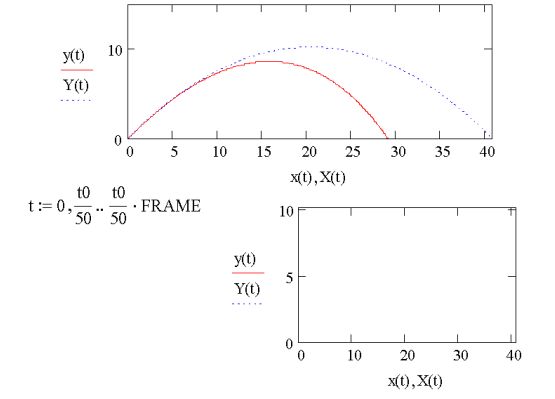
Рис. 1 Графіки траєкторій, розрахованих для випадків 1 і 2.
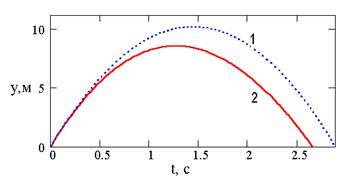
На рис. 2 і 3 наведено пояснювальні графіки, які дозволяють візуально оцінити відмінності при розрахунку балістичних кривих з врахуванням і без врахування опору повітря. З рис. 1, 2, 3 видно, що врахування опору повітря не тільки зменшує дальність (х – х0) і висоту (у – у0) польоту тіла, але й робить траєкторію польоту відмінною від параболічної: вона стає несиметричною.
Рис. 2. Графіки залежності дальності польоту від часу.
Рис. 3. Графіки залежності висоти польоту від часу. Порядок виконання роботи
Для побудови і анімації траєкторії руху в пакеті Mathcad створюємо документ, що містить послідовність наступних процедур: 1. Ввести прискорення вільного падіння g = 9,8 м/с2 і вихідні дані, задані викладачем – початкові координати х0, у0, початкову швидкість тіла v0, його масу m, коєфіціент опору повітря r, кут α, який утворює вектор швидкості з горизонтом. 2. Ввести параметри v0x, v0y, b за формулами (6), (10) і параметр t0 за формулою t0 = 2v0y/g. 3. Визначити границі зміни часу, обмеживши його максимальне значення величиною t0, і ввести аргумент t у вигляді ранжированої змінної (з кроком, наприклад, t0/100): t: = 0, 4. Ввести рівняння траєкторій: (8а), (8b) - для випадку 1 і (12а), (12b) - для випадку 2. При цьому для координат тіла, що відповідають цим випадкам, потрібно ввести різні позначення. Наприклад, для випадку 1 – х(t), у(t), для випадку 2 – Х(t), Y(t).
5. Побудувати графіки траєкторій, введених у п. 4. Для цього виконати послідовність таких операцій: 1) Лівою клавішею мишки натиснути там, де потрібно створити графік. 2) Послідовно відкрити Insert (Вставка), Graph (Графік) і вибрати у вікні, що з’явилося, X –Y Plot. Mathсad створить пустий графік з шістьма полями введення, по три на кожній осі. 3) Ввести у пусте поле, розташоване в середині горизонтальної осі, функції x(t) і Х(t), а у пусте поле біля середини вертикальної осі - y(t) i Y(t); ввести граничні значення функцій x(t) (x0 i xm = x(t0)) i y(t) (y0 i ym = y(t0/2)). 4) Натиснути клавішу F9. 6. Для розгляду руху тіла у динаміці потрібно, використовуючи документ, створений у п. 4, виконати послідовність таких дій: 1) Ввести змінну FRAME, замінивши максимальне значення змінної t, тобто t0, виразом t0 × де k – ціле число, k >> 1. 2) Послідовно вибрати пункти View (Вид), Animate (Анімація), що приведе до появи діалогового вікна Animate. 3) У діалоговому вікні, що з’явилося, у полі FRAME встановити нижню границю змінної FRAME і у полі TO – її верхню границю, вибравши для нижньої границі нуль, а для верхньої – число k. Змінна FRAME буде збільшуватись з oдиничним кроком від нижньої границі до верхньої. 4) У полі AT встановити швидкість відтворення кліпу. 5) Підготувати “пустий” графік і виділити його пунктирним прямокутником. 6) Натиснути кнопку Animate діалогового вікна. 7. Після створення анімаційного кліпу зберегти його як Windows AVI-файл; для цього натиснути кнопку Save As у діалоговому вікні. 8. Побудувати і проаналізувати графіки залежностей дальності і висоти польоту від часу для випадків 1 і 2.
Питання для самоперевірки 1. Який рух називається поступальним? 2. Що таке матеріальна точка? 3. Дати визначення швидкості поступального руху тіла. 4. Дати визначення середній і миттєвій швидкостям тіла. 5. Що характеризує тангенціальне прискорення? Як визначається його величина і напрямок? 6. Що характеризує нормальне прискорення? Як визначається його величина і напрямок? 7. Як можна охарактеризувати рух, коли відомо, що нормальне прискорення аn = 0, а тангенціальне прискорення at > 0? 8. Як можна охарактеризувати рух, коли відомо, що нормальне прискорення аn = const, а тангенціальне прискорення at = 0? 9. Запишіть і сформулюйте основне рівняння динаміки матеріальної точки. 10. Запишіть і сформулюйте закон Стокса.
Додаток
MATHCAD-PROGRAM g:=9.8 x0:=0 y0:=0 v0:=20 m:=0.5 r:=0.1 v0x:=v0×cos(a) v0y:=v0×sin(a)
Теоретичні відомості Обертальним рухом твердого тіла (системи) відносно нерухомої осі називається такий рух, під час якого всі точки тіла (системи) рухаються в площинах, перпендикулярних до осі обертання, і описують кола з центрами на цій осі.
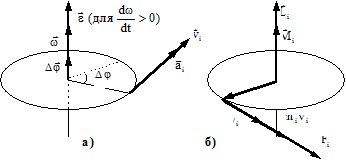
Рис. 1.
Кінематика та динаміка обертального руху характеризується відповідно кутом повороту s = jr, Динамічні характеристики обертального руху визначаються наступними виразами:
Взаємозв’язок між відповідними величинами додатково розкривається при графічному зображенні векторних величин, що розглядаються в лабораторній роботі (див. рис. 1: а – кінематика, б – динаміка). Основний закон динаміки обертального руху тіла відносно нерухомої осі обертання має наступний вигляд:
Для тіл правильної геометричної форми момент інерції простіше визначити аналітично, для тіл неправильної геометричної форми – експериментально. З експериментальних найбільш поширеними є методи, які основуються на використанні основного закону динаміки обертального руху, закону збереження та перетворення енергії та законів коливального руху.
Опис методу
У роботі використовується динамічний метод із застосуванням основного закону динаміки обертального руху. Маятник Обербека, момент інерції якого треба визначити, складається із закріпленого на горизонтальній осі шківа (рис. 2) з радіально розташованими стержнями, на яких симетрично закріплені чотири тягарці масами m1. На шків намотана нитка, один кінець якої закріплений до шківа, а на другому кінці підвішений тягарець масою m. Під час опускання тягарця m маятник Обербека під дією сили натягу нитки Основне рівняння динаміки обертального руху для маятника Обербека має вигляд: де r– радіус шківа. Моментом сили тертя нехтуємо. Напрямок вектора моменту
Прирівнявши праві частини рівнянь (1) та (2), отримаємо
звідки:
Робочу формулу для розрахунку моменту інерції J знайдемо, використавши величини h і t, які вимірюються в процесі експерименту, де h – шлях руху тягарця m по вертикалі, t – час його руху. Виразивши кутове прискорення e через лінійне прискорення точок a, які знаходяться на ободі шківа, зведемо задачу до знаходження лише a. Оскільки тягарець m рухається прямолінійно і рівноприскорено, то його шлях h, пройдений за час t, можна визначити за формулою:
Тоді кутове прискорення маятника: Підставивши значення a та e у рівняння (3), отримаємо:
Якщо врахувати можливі числові значення величин в нашому експерименті (h» 1 м, t» 10 c Þ gt2/2h» 500), то в формулі (4) можна знехтувати одиницею і отримати спрощений вираз: Формула (5) є робочою для експериментального визначення моменту інерції маятника Обербека. В роботі виконуються прямі вимірювання величин h і t, значення величин m, m1 та r наведені в паспорті установки.
Порядок виконання роботи
1. Перевірити роботу маятника Обербека, зробивши декілька пробних запусків установки. Звернути увагу на вільність обертання шківа та опускання тягарця масою m, а також на збалансованість маятника. При необхідності відрегулювати установку (можливо з допомогою лаборанта). 2. Вибрати певну довжину шляху h руху тягарця m, яка буде однаковою для всіх вимірів. 3. Намотати нитку на шків так, щоб нижня частина тягарця знаходилась на рівні початку відліку шляху (висоти) руху тягарця. Відпустити тягарець m і одночасно ввімкнути секундомір. Зробити 5 вимірів. Записати в таблицю 1 значення h і t. 4. Зняти всі чотири тягарці m1 і повторити експеримент для того ж самого шляху h. Результати вимірювання часу t' занести до таблиці 1. Обчислення середніх значень 1. Обчислити середнє значення часу t та t', моменту інерції маятника з тягарцями J і маятника без тягарців J' за робочою формулою (5). Для моделі абсолютно твердого тіла, яка використовується для розгляду обертального руху тіла, при обчисленні моментів інерції використовується адитивність (незалежне складання) моментів інерції всіх матеріальних точок тіла або, таким чином, будь-яких його частин. Тому момент інерції маятника Обербека J дорівнює сумі моментів інерції маятника без тягарців J' і моментів інерції самих тягарців J0е: J = J' + J0е, звідки експериментальне значення величини моменту інерції чотирьох тягарців J0е = J - J'. З іншого боку, якщо розглядати тягарці як матеріальні точки, то теоретичне значення їх моменту інерції J0т = 4m1R2 , де R – відстань від осі обертання до центру тяжіння тягарців масами m1.
Таблиця 1 Результати вимірювань та вихідні дані для розрахунків
h=.....; m=..... ±.....; m1=..... ±.....; r=..... ±.....; R=.....;
2. Обчислити теоретичне значення моменту інерції тягарців J0т та порівняти його з експериментальним.
Питання для самоперевірки 1. Навести формулу, що пов’язує швидкість поступального руху з кутовою швидкістю. 2. Що таке кутове прискорення? 3. Що таке момент сили, від чого він залежить і за яким правилом визначається напрямок вектора моменту сили? 4. Що таке момент імпульсу і від чого він залежить? 5. Дати визначення моменту інерції матеріальної точки і твердого тіла. 6. Від чого залежить момент інерції тіла? 7. Запишіть основне рівняння динаміки обертального руху тіла (загальний і окремий випадок). 8. Як зміниться момент інерції диска відносно вісі обертання, що проходить через його центр мас, якщо радіус диска збільшити у два рази? 9. Як зміниться момент інерції диска відносно вісі обертання, що проходить через його центр мас, якщо масу диска збільшити у два рази? 10. Швидше чи повільніше буде обертатися уся система, якщо тягарці на спицях маятника Обербека розмістити ближче до вісі обертання? Відповідь пояснити, використовуючи відповідні формули.
Лабораторна робота № 3 Теоретичні відомості Питомою теплоємністю речовини називають величину, яка дорівнює кількості теплоти, що необхідно надати одиниці маси речовини для підвищення її температури на 1 K. Для газів ця величина залежить від умов, при яких проходить нагрівання – при сталому об’ємі чи при сталому тиску, і тому виражається відповідно питомою теплоємністю при сталому об’ємі cv та питомою теплоємністю при сталому тиску cp. cv і cp мають різні значення для одного й того ж газу, оскільки кількість теплоти, надана газу при різних умовах, розподіляється по-різному. Згідно з першим законом термодинаміки під час нагрівання при сталому об’ємі вся теплота витрачається тільки на збільшення внутрішньої енергії речовини, а під час нагрівання при сталому тиску підведена теплота витрачається на збільшення внутрішньої енергії газу та на виконання роботи проти зовнішніх сил. Безпосередньо виміряти cp і особливо cv важко, бо теплоємність газу становить мізерну долю теплоємності посудини, в якій міститься газ, тому вимірювання виконується неточно. Простіше виміряти відношення cp/cv, яке надасть величину показника адіабати - g. Величина cp/cv = g входить до рівняння Пуассона, яке описує адіабатичний процес зміни стану ідеального газу: pVg = const. (1)
Співвідношення cp/cv = g залежить тільки від числа степенів вільності молекул, що входять до складу газу:
де i– число степенів вільності. Для одноатомного газу i = 3, двоатомного i = 5, триатомного та багатоатомного i = 6. Завдання даної роботи: знайти значення відношення питомих теплоємностей для повітря, яке вважається двоатомним газом. Опис методу
Метод, який використовується в цій роботі, був запропонований Клеманом і Дезормом. В основі його – використання адіабатичного розширення газу. Адіабатичним називається процес, який проходить без теплообміну з навколишнім середовищем. Перший закон термодинаміки для адіабатичного процесу має наступний вигляд:
A + DU = 0, або A = -DU,
де DU – зміна внутрішньої енергії газу; A – робота, виконана газом. З цієї формули видно, що робота розширення виконуватиметься за рахунок зміни внутрішньої енергії газу; температура газу при цьому знизиться. Під час же адіабатичного стискання газу його температура підвищиться. Якщо об’єм газу змінюється досить швидко, то внаслідок того, що теплопровідність газу невелика, процес можна розглядати як дуже близький до адіабатичного. Прослідкуємо за послідовністю процесів, що відбуваються у даному лабораторному експерименті та виведемо формулу для обчислення g.
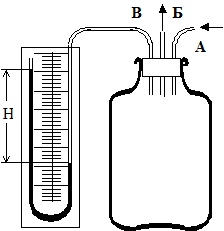
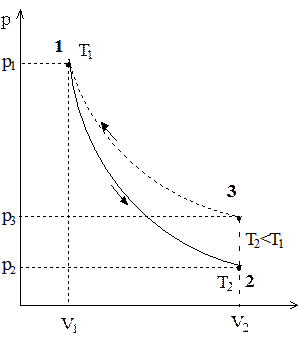
У скляний балон (рис. 1) за допомогою насосу нагнітають повітря, створюючи всередині балону тиск, вищий за атмосферний. Цей стан відповідатиме початку експерименту (рис. 2, точка 1) і описується параметрами p1, V1, T1. Швидке розширення газу можна вважати з достатнім наближенням адіабатичним. Тому, відкриваючи кран на короткий час, протягом якого тиск всередині балону досягне атмосферного, можна вважати, що газ перейшов до нового стану, який характеризується параметрами p2, V2, T2<T1 (рис. 2, точка 2). При цьому температура T2 газу після адіабатичного розширення буде меншою від T1. Параметри станів 1 та 2 зв’язані рівнянням адіабатичного процесу. Через 2-3 хвилини після перекривання крану газ нагріється до температури навколишнього повітря T1. Але оскільки під час цього нагрівання V2 залишиться незмінним, то тиск у балоні підвищиться до p3. Новий стан газу характеризується параметрами p3, V2, T1 (рис. 2, точка 3).
Порівнявши кінцевий стан газу (точка 3) з початковим (точка 1), бачимо, що вони знаходяться при однаковій температурі. Отже, за законом Бойля – Маріотта:
p3V2 = p1V1. (2)
Виконаємо деякі перетворення в цьому рівнянні. Піднесемо його до степеня g і поділимо на рівняння (1):
Прологарифмуємо рівняння (3):
Умови експерименту надають змогу спростити розрахункову формулу. А саме, якщо позначити початковий тиск у балоні p1, початкову різницю рівнів рідини в манометрі H, то: p1 = p2 + bH, (5) де p2 – атмосферний тиск; b – коефіцієнт переходу від різниці рівнів рідини до тиску. Для тиску p3 різницю рівнів позначимо h, тоді: p3 = p2 + bh. (6) Визначивши
p3 = p1 - b(H-h). (7)
Підставивши p2 і p3 у рівняння (4), знайдемо:
Величини Формула (8) буде розрахунковою для визначення g. Порядок виконання роботи
1. Закрити трубку Б (див. рис. 1) і повільно нагнітати повітря в балон, доки різниця рівнів рідини в манометрі не стане рівною 20-30 см. 2. Виміряти значення різниці рівнів рідини H в манометрі. 3. Відкрити трубку Б, випустити з балона надлишок повітря і знову закрити. Проміжок часу з моменту відкриття до моменту закриття дорівнює 1-2 с. 4. При закритій трубці Б чекати 2-3 хв. і виміряти нове значення різниці рівнів рідини h у манометрі. Якщо різниця рівнів рідини в манометрі при вимірах постійно зменшується, то потрібно вжити заходів для забезпечення герметичності системи. Простіше - закрити (перетиснути) трубку А, щоб запобігти проходженню повітря через клапан насосу. 5. Експеримент повторити 5 разів, зберігаючи одне й те саме значення H та вимірюючи кожен раз значення h. Результати вимірів занести до таблиці 1.
Таблиця 1 Обчислення середніх значень 1. Обчислити середнє значення <h>, результат внести до табл. 1. 2. За результатами вимірювання H та середнім значенням <h> визначити експериментальне значення величини <g>. 3. Вважаючи повітря двоатомним газом, прийняти i = 5. Обчислити теоретичне значення величини g. 4. Записати результат вимірювання g та зробити висновок про його відповідність теоретичному значенню.
Питання для самоперевірки 1. Який газ називається ідеальним? 2. Що таке рівняння стану і який вигляд воно має для ідеального газу? 3. Сформулювати перший закон термодинаміки. 4. Що називають кількістю степенів вільності молекули? 5. Скільки степенів вільності використовують для характеристики повітря? Відповідь пояснити. 6. Який процес називають адіабатичним? 7. Дати визначення питомій та молярній теплоємності. Пояснити зв’язок між ними. 8. Чому необхідно зачекати декілька хвилин після накачування повітря в балон і після випускання його надлишку з балону? 9. Чому поступово зростає тиск в закритому балоні після того, як надлишок повітря з нього було випущено? 10. Як для газу можна теоретично розрахувати показник адіабати γ?
Лабораторна робота № 4 Дослідження електростатичного поля
Мета роботи: експериментально дослідити конфігурацію електростатичного поля між металевими електродами. Прилади та обладнання: джерело постійної напруги, пластина з електродами, вольтметр, гальванометр, потенціометр, металевий зонд, перемикач, з’єднувальні провідники, папір.
Теоретичні відомості Нерухомий заряд створює в навколишньому просторі електростатичне поле, яке проявляється за силовою дією на вміщений у будь-яку точку поля інший заряд. Електростатичне поле має дві характеристики - силову та енергетичну. Кількісна силова характеристика називається напруженістю
Електростатичне поле зручно зображувати у вигляді силових ліній. Густина силових ліній характеризує числове значення напруженості, а дотичні до них у кожній точці збігаються з напрямком вектора напруженості. Силові лінії починаються на позитивних зарядах і закінчуються на негативних, вони ніде не перетинаються, тому що в кожній точці поля вектор Енергетичною характеристикою електростатичного поля є потенціал. Ця величина чисельно дорівнює роботі A, яку виконують сили поляпри переміщенні одиничного позитивного точкового заряду з даної точки поля в нескінченість:
Різниця потенціалів (напруга) між двома точками поля визначається роботою по переміщенню одиничного позитивного точкового заряду з однієї точки простору в іншу:
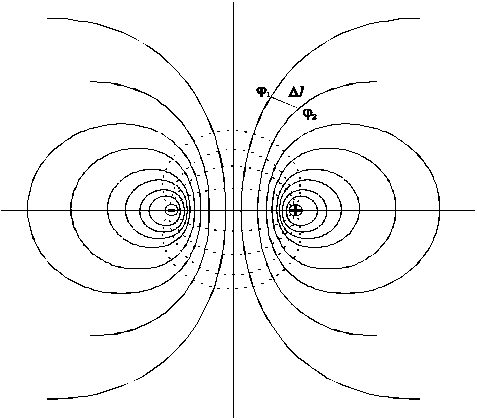
Геометричне місце точок з однаковим потенціалом називається еквіпотенціальною поверхнею. Лінії напруженості в кожній точці ортогональні до еквіпотенціальних поверхонь. Дійсно, при переміщенні заряду вздовж еквіпотенціальної поверхні робота, яка згідно (3) визначає різницю потенціалів двох точок поля, дорівнює нулю (потенціал не змінюється). З іншого боку за визначенням DA = F.Dl.cosa = 0. Тут переміщення Dl відбувається вздовж еквіпотенціальної поверхні, а сила Зв'язок між напруженістю поля та потенціалом виражається співвідношенням: На рис.1 зображений переріз картини розподілу еквіпотенціальних поверхонь і силових ліній площиною рисунка для електростатичного поля двох протилежно заряджених кульок. У цьому випадку за напрямок зміни потенціалу вибираємо напрямок силової лінії, тому
Рис. 1.
Опис методу Можна показати, що розподіл поля в непровідному середовищі (вакуум чи повітря) зберігається, якщо положення електродів не змінювати і простір між ними заповнити електролітом. Але дослідження електростатичного поля та його характеристик у провідному середовищі значно простіше, ніж у непровідному. В цьому випадку достатньо виміряти електричні потенціали точок поля, користуючись методом зонда (металевого щупа). Змінюючи потенціал на зонді, можна домогтись того, що сила струму через зонд буде дорівнювати нулю. Це відбувається тоді, коли потенціал в досліджуваній точці поля дорівнює потенціалу на зонді. У цій роботі досліджується конфігурація електростатичного поля між двома плоскими електродами. В якості електроліту використовується зволожений папір. Електрична схема установки для проведення експерименту показана на рис. 2. Плоска прямокутна пластина з діелектрика є основною в установці. На ній розміщують вологий аркуш паперу і щільно його притискають до електродів. Від джерела постійного струму на електроди пластини безпосередньо або через потенціометр подають напругу. При цьому між електродами виникає постійне електричне поле з відповідним розподілом потенціалу, який вимірюють методом зонда. Із схеми видно, що металевий зонд з'єднаний через гальванометр з середньою точкою потенціометра. Такий самий потенціал можна знайти на папері між електродами. Переміщуючи вздовж пластини металевий зонд, знаходять таке його положення, при якому гальванометр покаже нуль. Тоді потенціал у даній точці пластини дорівнює потенціалу, що його показує вольтметр, тобто відповідна різниця потенціалів дорівнює нулю, і струм через гальванометр не протікає. Повторюючи цю опер
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-10; просмотров: 95; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.205.161 (0.017 с.) |

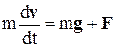 , (1)
, (1)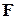 - cила опору повітря. Згідно з законом Стокса:
- cила опору повітря. Згідно з законом Стокса: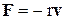 , (2)
, (2)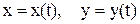 координати тіла у довільний момент часу t. У проекціях на координатні вісі другий закон Ньютона (рівняння руху) набуває вигляду:
координати тіла у довільний момент часу t. У проекціях на координатні вісі другий закон Ньютона (рівняння руху) набуває вигляду: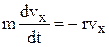 , (3а)
, (3а)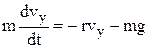 (3b)
(3b)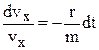 , (4а)
, (4а)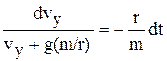 . (4b)
. (4b)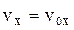 ,
, 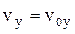 , (5)
, (5)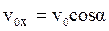 ,
, 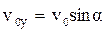 (6)
(6)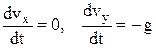 ,
,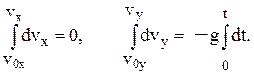
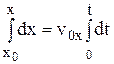 ,
,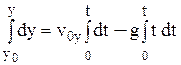 .
.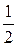 gt 2. (8b)
gt 2. (8b)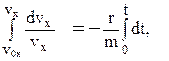

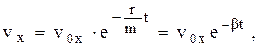 (9)
(9)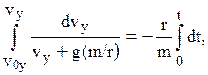
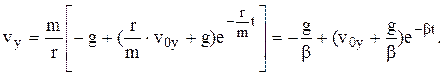 (11)
(11) формули (9) і (11) переходять у формули (7).
формули (9) і (11) переходять у формули (7).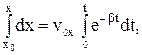
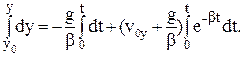
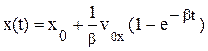 , (12a)
, (12a)
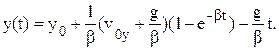 (12b)
(12b)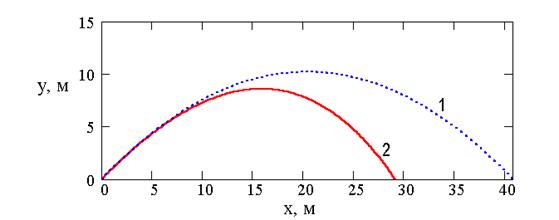
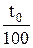 ..t0.
..t0.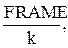
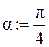
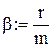
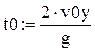
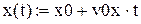
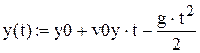
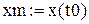
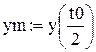
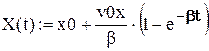
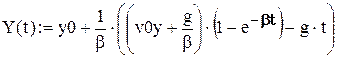
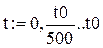
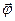 , приростом кута повороту
, приростом кута повороту 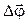 , кутовою швидкістю
, кутовою швидкістю 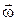 , кутовим прискоренням
, кутовим прискоренням 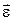 , моментом інерції J, моментом сили
, моментом інерції J, моментом сили 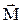 , моментом імпульсу
, моментом імпульсу 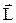 , які виконують таку саму роль для обертального руху, як і відповідні величини – шлях S, переміщення
, які виконують таку саму роль для обертального руху, як і відповідні величини – шлях S, переміщення 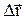 , швидкість
, швидкість 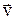 , прискорення
, прискорення 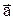 та маса m, сила
та маса m, сила 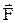 , імпульс
, імпульс 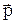 - для поступального руху. Зв’язок між лінійними і відповідними кутовими кінематичними величинами здійснюється через радіус обертання r (радіус-вектор
- для поступального руху. Зв’язок між лінійними і відповідними кутовими кінематичними величинами здійснюється через радіус обертання r (радіус-вектор 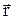 ) таким чином:
) таким чином: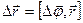 ,
, 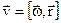 ,
, 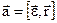 .
.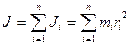 ,
, 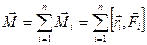 ,
,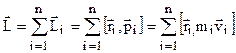 .
.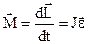 . (1)
. (1)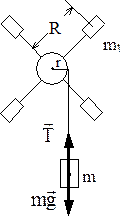
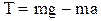 приводиться в рівноприскорений обертальний рух.
приводиться в рівноприскорений обертальний рух.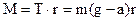 , (2)
, (2)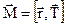 .
.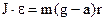 ,
,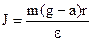 . (3)
. (3)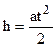 , звідки
, звідки 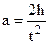 .
.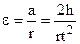 .
.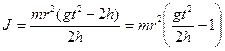 . (4)
. (4)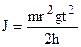 . (5)
. (5)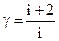 ,
,
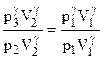 Þ
Þ 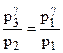 Þ
Þ 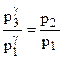 Þ
Þ 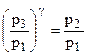 . (3)
. (3)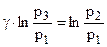 Þ
Þ 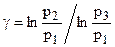 . (4)
. (4)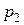 із рівняння (5) і підставивши його в (6), отримаємо:
із рівняння (5) і підставивши його в (6), отримаємо: .
.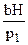 та
та 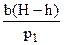 набагато менші за одиницю, тому, використавши наближену формулу ln (1-x)»-x, справедливу для малих x, отримаємо:
набагато менші за одиницю, тому, використавши наближену формулу ln (1-x)»-x, справедливу для малих x, отримаємо: 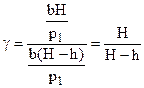 . (8)
. (8)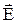 . Ця величина векторна і в даній точці поля чисельно дорівнює силі
. Ця величина векторна і в даній точці поля чисельно дорівнює силі 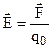 . (1)
. (1)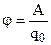 . (2)
. (2)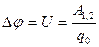 . (3)
. (3)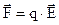 спрямована вздовж силової лінії. Обидві ці величини не дорівнюють нулю, таким чином, cos a = 0 і відповідно a = 900.
спрямована вздовж силової лінії. Обидві ці величини не дорівнюють нулю, таким чином, cos a = 0 і відповідно a = 900.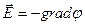 , де
, де 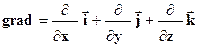 - градієнт, що пов’язує скалярну величину (потенціал) з векторною величиною (напруженістю електричного поля). Знак "-" вказує на те, що вектор напруженості поля спрямований в бік зменшення потенціалу.
- градієнт, що пов’язує скалярну величину (потенціал) з векторною величиною (напруженістю електричного поля). Знак "-" вказує на те, що вектор напруженості поля спрямований в бік зменшення потенціалу.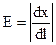 .
.