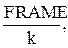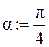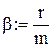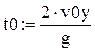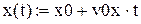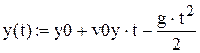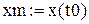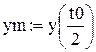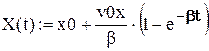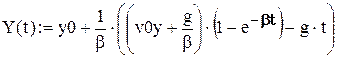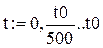Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Національний транспортний університетСодержание книги
Поиск на нашем сайте
МЕТОДИЧНІ ВКАЗІВКИ До виконання лабораторних робіт З використанням комп’ютерного експерименту з дисципліни „Концепції сучасного природознавства” для студентів спеціальності 8.050201 „Менеджмент організацій” В рамках кредитно–модульної системи Організації навчального процесу
ЗАТВЕРДЖЕНО на засіданні навчально–методичної Ради Національного транспортного університету Протокол №___від______________2007 р.
Київ НТУ 2007 Методичні вказівки до виконання лабораторних робіт з використанням комп’ютерного експерименту з дисципліни „Концепції сучасного природознавства” для студентів спеціальності 8.050201 „Менеджмент організацій” в рамках кредитно–модульної системи організації навчального процесу // Укл.: Гололобов Ю.П., Іщенко Р.М., Шатній Т.Д. – К.: НТУ, 2007. – 37 с.
Укладачі: Гололобов Ю.П. – доктор фіз.-мат. наук Іщенко Р.М. – кандидат фіз.-мат. наук Шатній Т.Д. – кандидат фіз.-мат. наук Відповідальний за випуск: Іщенко Р.М.
Вступ
На сучасному етапі розвитку суспільства бути кваліфікованим спеціалістом неможливо без знань основних концепцій сучасного природознавства. Формування наукового світогляду та наукового стилю мислення у значній мірі залежить від засвоєння найбільш важливих досягнень природознавства як сукупності наук про природу. Кожен студент, який в подальшому збирається стати менеджером, економістом чи юристом, щоб почувати себе високоосвіченою людиною, повинен знати що таке теорія відносності, квантова механіка, синергетика та інші науки. Навчальною програмою з дисципліни „Концепції сучасного природознавства” окрім лекційного курсу передбачено виконання студентами циклу лабораторних робіт. Такий підхід сприяє формуванню навичок щодо використання одержаних знань для розв’язку практичних задач, зокрема техніко-інженерного напрямку. Кредитно–модульна система організації навчального процесу, яка впроваджується в Національному транспортному університеті, передбачає використання як традиційних методів виконання лабораторних робіт (проведення фізичного експерименту), так і новітніх методів, зокрема, використання комп’ютерного експерименту. Тому в даних методичних вказівках до виконання лабораторних робіт з дисципліни „Концепції сучасного природознавства” для студентів спеціальності „Менеджмент організацій” разом з роботами, які виконуються безпосередньо при проведені фізичного експерименту, представлено лабораторну роботу „Моделювання криволінійного руху тіла”, що виконується з використанням комп’ютерного експерименту. Для покращення засвоєння навчального матеріалу в методичних вказівках після кожної лабораторної роботи наведено питання для самоперевірки знань студентів.
Лабораторна робота № 1 (з використанням комп’ютерного експерименту) Моделювання криволінійного руху тіла
Мета роботи: вивчити основні положення кінематики і динаміки матеріальної точки та закономірності руху тіл в однорідному полі тяжіння. Дослідити вплив опору повітря на форму траєкторії, дальність і висоту польоту.
Теоретичні відомості Нехай тіло масою m кинуто під кутом α до горизонту зі швидкістю v0. Знайдемо його траєкторію з врахуванням опору повітря і порівняємо її з траєкторію, отриманою при нехтуванні опором повітря. Вважаючи тіло матеріальною точкою, запишемо для нього другий закон Ньютона:
де g - прискорення вільного падіння, v = v (t) - швидкість тіла у довільній момент часу t,
де r – коефіцієнт опору (він залежить від розмірів і форми тіла та від властивостей середовища, в якому тіло рухається). Виберемо декартову систему координат так, щоб вектор початкової швидкості знаходився у площині Oxy, спрямуємо вісь Oy вертикально вгору перпендикулярно поверхні землі і позначимо через
або
Якщо у момент кидання t = 0 тіло знаходиться у точці з координатами х0, у0, то початкові умови задачі є такими:
при t = 0 x = x0, y = y0, де – проекції початкової швидкості на вісі координат. Розв’яжемо отримані диференціальні рівняння для двох випадків. 1. Опором повітря нехтуємо, r = 0. Запишемо для цього випадку рівняння (3а, 3b):
та інтегруємо їх з врахуванням початкових умов (5):
В результаті отримуємо відомі формули: vx = v0x, vy = v0y – gt, (7)
згідно з якими рух тіла у горизонтальному напрямку є рівномірним, а у вертикальному – рівноприскореним. Знайдемо траєкторію тіла у параметричному вигляді: х = х (t), у = у (t). Для цього врахуємо, що vx = dx/dt, vy = dy/dt, перепишемо рівняння (7) у вигляді:
dx = v0x·dt, dу = v0y·dt – gt·dt
і проінтегруємо їх з врахуванням початкових умов (5):
В результаті отримуємо траєкторію тіла: x(t) = x0 + v0xt, (8a) y(t) = y0 + v0yt –
2. Враховуємо силу опору повітря, r > 0. У цьому випадку інтегруємо рівняння (4а):
і знаходимо:
де β = r/m. (10)
Аналогічно, інтегруючи рівняння (4b):
знаходимо:
Зауважимо, що при Для знаходження траєкторії тіла у параметричному вигляді інтегруємо з врахуванням початкових умов (5) рівняння (9) і (11):
В результаті знаходимо траєкторію тіла з врахуванням сили опору повітря:
Приклад
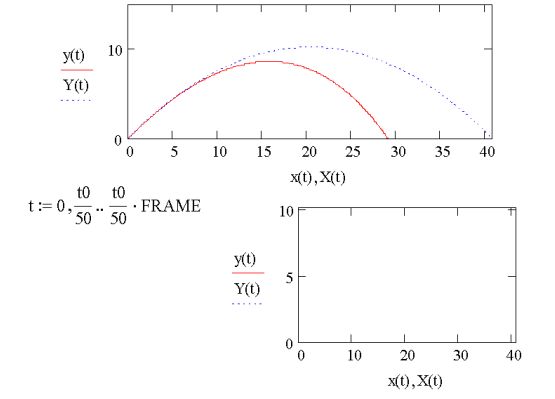
Рис. 1 Графіки траєкторій, розрахованих для випадків 1 і 2.
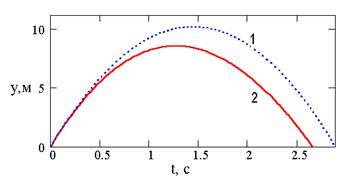
На рис. 2 і 3 наведено пояснювальні графіки, які дозволяють візуально оцінити відмінності при розрахунку балістичних кривих з врахуванням і без врахування опору повітря. З рис. 1, 2, 3 видно, що врахування опору повітря не тільки зменшує дальність (х – х0) і висоту (у – у0) польоту тіла, але й робить траєкторію польоту відмінною від параболічної: вона стає несиметричною.
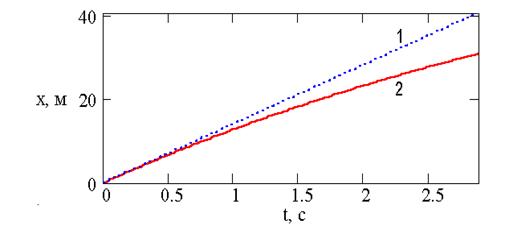
Рис. 2. Графіки залежності дальності польоту від часу.
Рис. 3. Графіки залежності висоти польоту від часу. Порядок виконання роботи
Для побудови і анімації траєкторії руху в пакеті Mathcad створюємо документ, що містить послідовність наступних процедур: 1. Ввести прискорення вільного падіння g = 9,8 м/с2 і вихідні дані, задані викладачем – початкові координати х0, у0, початкову швидкість тіла v0, його масу m, коєфіціент опору повітря r, кут α, який утворює вектор швидкості з горизонтом. 2. Ввести параметри v0x, v0y, b за формулами (6), (10) і параметр t0 за формулою t0 = 2v0y/g. 3. Визначити границі зміни часу, обмеживши його максимальне значення величиною t0, і ввести аргумент t у вигляді ранжированої змінної (з кроком, наприклад, t0/100): t: = 0, 4. Ввести рівняння траєкторій: (8а), (8b) - для випадку 1 і (12а), (12b) - для випадку 2. При цьому для координат тіла, що відповідають цим випадкам, потрібно ввести різні позначення. Наприклад, для випадку 1 – х(t), у(t), для випадку 2 – Х(t), Y(t).
5. Побудувати графіки траєкторій, введених у п. 4. Для цього виконати послідовність таких операцій: 1) Лівою клавішею мишки натиснути там, де потрібно створити графік. 2) Послідовно відкрити Insert (Вставка), Graph (Графік) і вибрати у вікні, що з’явилося, X –Y Plot. Mathсad створить пустий графік з шістьма полями введення, по три на кожній осі. 3) Ввести у пусте поле, розташоване в середині горизонтальної осі, функції x(t) і Х(t), а у пусте поле біля середини вертикальної осі - y(t) i Y(t); ввести граничні значення функцій x(t) (x0 i xm = x(t0)) i y(t) (y0 i ym = y(t0/2)). 4) Натиснути клавішу F9. 6. Для розгляду руху тіла у динаміці потрібно, використовуючи документ, створений у п. 4, виконати послідовність таких дій: 1) Ввести змінну FRAME, замінивши максимальне значення змінної t, тобто t0, виразом t0 × де k – ціле число, k >> 1. 2) Послідовно вибрати пункти View (Вид), Animate (Анімація), що приведе до появи діалогового вікна Animate. 3) У діалоговому вікні, що з’явилося, у полі FRAME встановити нижню границю змінної FRAME і у полі TO – її верхню границю, вибравши для нижньої границі нуль, а для верхньої – число k. Змінна FRAME буде збільшуватись з oдиничним кроком від нижньої границі до верхньої. 4) У полі AT встановити швидкість відтворення кліпу. 5) Підготувати “пустий” графік і виділити його пунктирним прямокутником. 6) Натиснути кнопку Animate діалогового вікна. 7. Після створення анімаційного кліпу зберегти його як Windows AVI-файл; для цього натиснути кнопку Save As у діалоговому вікні. 8. Побудувати і проаналізувати графіки залежностей дальності і висоти польоту від часу для випадків 1 і 2.
Питання для самоперевірки 1. Який рух називається поступальним? 2. Що таке матеріальна точка? 3. Дати визначення швидкості поступального руху тіла. 4. Дати визначення середній і миттєвій швидкостям тіла. 5. Що характеризує тангенціальне прискорення? Як визначається його величина і напрямок? 6. Що характеризує нормальне прискорення? Як визначається його величина і напрямок? 7. Як можна охарактеризувати рух, коли відомо, що нормальне прискорення аn = 0, а тангенціальне прискорення at > 0? 8. Як можна охарактеризувати рух, коли відомо, що нормальне прискорення аn = const, а тангенціальне прискорення at = 0? 9. Запишіть і сформулюйте основне рівняння динаміки матеріальної точки. 10. Запишіть і сформулюйте закон Стокса.
Додаток
MATHCAD-PROGRAM g:=9.8 x0:=0 y0:=0 v0:=20 m:=0.5 r:=0.1 v0x:=v0×cos(a) v0y:=v0×sin(a)
|
|||||||||||||
|
Последнее изменение этой страницы: 2021-03-10; просмотров: 70; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.26.112 (0.007 с.) |

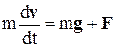 , (1)
, (1)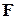 - cила опору повітря. Згідно з законом Стокса:
- cила опору повітря. Згідно з законом Стокса: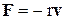 , (2)
, (2)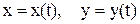 координати тіла у довільний момент часу t. У проекціях на координатні вісі другий закон Ньютона (рівняння руху) набуває вигляду:
координати тіла у довільний момент часу t. У проекціях на координатні вісі другий закон Ньютона (рівняння руху) набуває вигляду: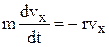 , (3а)
, (3а)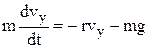 (3b)
(3b)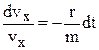 , (4а)
, (4а)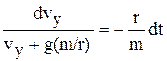 . (4b)
. (4b)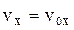 ,
, 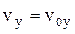 , (5)
, (5)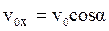 ,
, 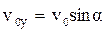 (6)
(6)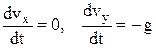 ,
,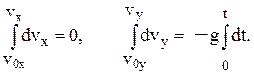
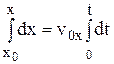 ,
,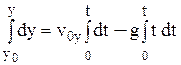 .
.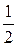 gt 2. (8b)
gt 2. (8b)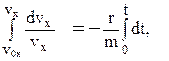

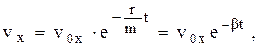 (9)
(9)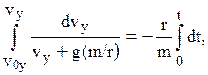
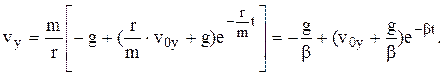 (11)
(11)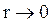 формули (9) і (11) переходять у формули (7).
формули (9) і (11) переходять у формули (7).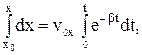
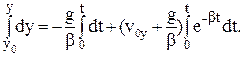
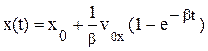 , (12a)
, (12a)
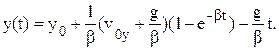 (12b)
(12b)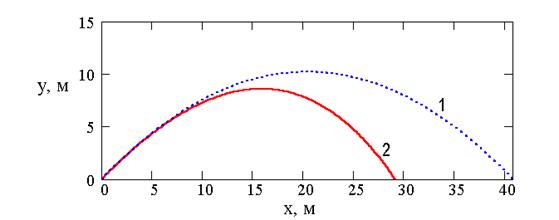
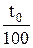 ..t0.
..t0.