
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Блок-схема метода простых итераций.Содержание книги
Поиск на нашем сайте
Программа. Нелинейное уравнение. Метод простых итераций function DATA global a b eps n_plot_dots; a=1; b=3; eps=0.01; n_plot_dots=100; end
function [ fx ] = f(x) fx=x.^2-5; end
function [ fx ] = fp(x) fx=x.*2; end
function [ x,fx ] = fun_Nelin_Prost_Iterac(a,b,eps) if abs(fp(b))>abs(fp(a)) beta=-2/fp(b); x=b; else beta=-2/fp(a); x=a; end %if for i=1:100 h=beta*f(x); x=x+h; if abs(h)<=eps i break; end%if end%for i fx=f(x); end % function
function GLAV_Nelin_Prost_Iterac global a b eps x fx n_plot_dots; DATA; [ x,fx ] = fun_Nelin_Prost_Iterac(a,b,eps); REPORT; end
function REPORT global a b eps x fx n_plot_dots; disp('Nelin Prost Iterac'); disp(' '); disp(['a = ' num2str(a,'%10.5f') ]); disp(['b = ' num2str(b,'%10.5f') ]); disp(['eps = ' num2str(eps,'%10.5f') ]); disp('Results'); disp(['x = ' num2str(x,'%10.5f') ]); disp(['fx = ' num2str(fx,'%10.5f') ]); h=(b-a)/(n_plot_dots-1); for i=1:n_plot_dots if i==1 xmas(i)=a; else xmas(i)=xmas(i-1)+h; end %if fmas(i)=f(xmas(i)); end disp(' i x fx '); disp(' ______________________________') i=0; for i=1:length(xmas) xx=xmas(i); ffx=fmas(i); disp(sprintf('%10.3f\t%10.3f\t %10.3f',i,xx,ffx)); end %for plot(xmas,fmas,'r.'); grid on; xlabel('x'); ylabel('y'); title('Nelin Prost Iterac'); end Метод Ньютона или касательных. Пусть известно некоторое приближение x(k-1) к решению x* уравнения f(x)=0. Тогда исходное уравнение можно записать в виде: f(x(k-1)+∆x(k-1))=0 где ∆x(k-1)= x* -x(k-1) и x* = x(k-1)+∆x(k-1). Разложим функцию в ряд Тейлора и ограничимся линейными членами f(x(k-1)+∆x(k-1)) = f(x(k-1))+f′(x(k-1))∆x(k-1) = 0 откуда На каждой итерации, за новое приближение к корню x(k) принимается точка пересечения касательной к графику, построенной в точке f(x(k-1)) с осью абсцисс x: Алгоритм 1) Задаем функцию f(x) отрезок [a;b] и точность e. За начальное приближение x принимаем одну из границ заданного отрезка [a,b] x=a. 2) Вычисляем значение шага h= f(x)/f′(x) и новое приближение, как x = x-h. 3) Проверяем условие окончания если | h | £ e, то выводим последнее значение x и f(x). Иначе перейдем на пункт 2 Блок-схема метода касательных (Ньютона)
Программа. Нелинейное уравнение. Метод Ньютона (касательных) function DATA global x0 eps n_plot_dots; x0=3; eps=0.01; n_plot_dots=100; end
function [ fx ] = f(x) fx=x.^2-5; end
function [ fx ] = fp(x) fx=x.*2; end
function [ x,fx ] = fun_Nelin_Newton(x0,eps) x=x0; for i=1:100 h=f(x)/fp(x); x=x-h; if abs(h)<=eps i break; end %if end %for i fx=f(x); end % function
function GLAV_Nelin_Newton global x0 eps n_plot_dots; DATA; [ x,fx ] = fun_Nelin_Newton(x0,eps); REPORT; end
function REPORT global x0 eps x fx n_plot_dots; disp('Nelin Newton'); disp(' '); disp(['x0 = ' num2str(x0,'%10.5f') ]); disp(['eps = ' num2str(eps,'%10.5f') ]); disp('Results'); disp(['x = ' num2str(x,'%10.5f') ]); disp(['fx = ' num2str(fx,'%10.5f') ]); a=x-2; b=x+2; h=(b-a)/(n_plot_dots-1); for i=1:n_plot_dots if i==1 xmas(i)=a; else xmas(i)=xmas(i-1)+h; end %if fmas(i)=f(xmas(i)); end disp(' i x fx '); disp(' ______________________________') i=0; for i=1:length(xmas) xx=xmas(i); ffx=fmas(i); disp(sprintf('%10.3f\t%10.3f\t %10.3f',i,xx,ffx)); end %for plot(xmas,fmas,'r.'); grid on; xlabel('x'); ylabel('y'); title('Nelin Newton'); end
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 123; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.219.203 (0.008 с.) |

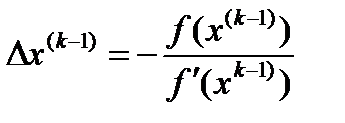 , и тогда
, и тогда 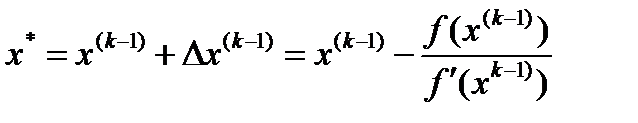 Полученное значение принимаем за новое приближение к решению. Тогда итерационную формулу запишем как:
Полученное значение принимаем за новое приближение к решению. Тогда итерационную формулу запишем как: 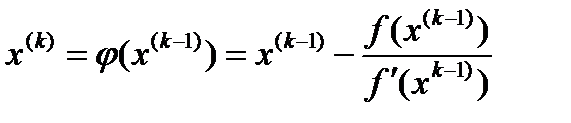
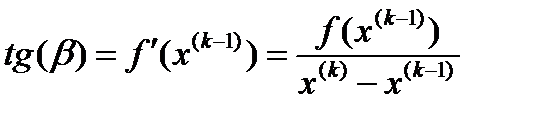 , тогда
, тогда 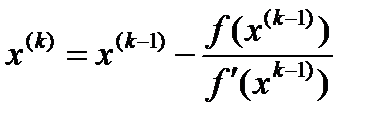 За начальное приближение к корню x(0) принимаем одну из границ отрезка [a; b], содержащего один корень.
За начальное приближение к корню x(0) принимаем одну из границ отрезка [a; b], содержащего один корень.


