Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обыкновенные дифференциальные уравнения и системы.
Дифференциальным уравнением n-го порядка называется уравнение: H(t, x, x’, x’’, …, x(n))=0 Решением дифференциального уравнения называется функция x(t), которая обращает уравнение в тождество. Системой дифференциальных уравнений n-го порядка называется система вида:
Системой линейных дифференциальных уравнений называют систему вида:
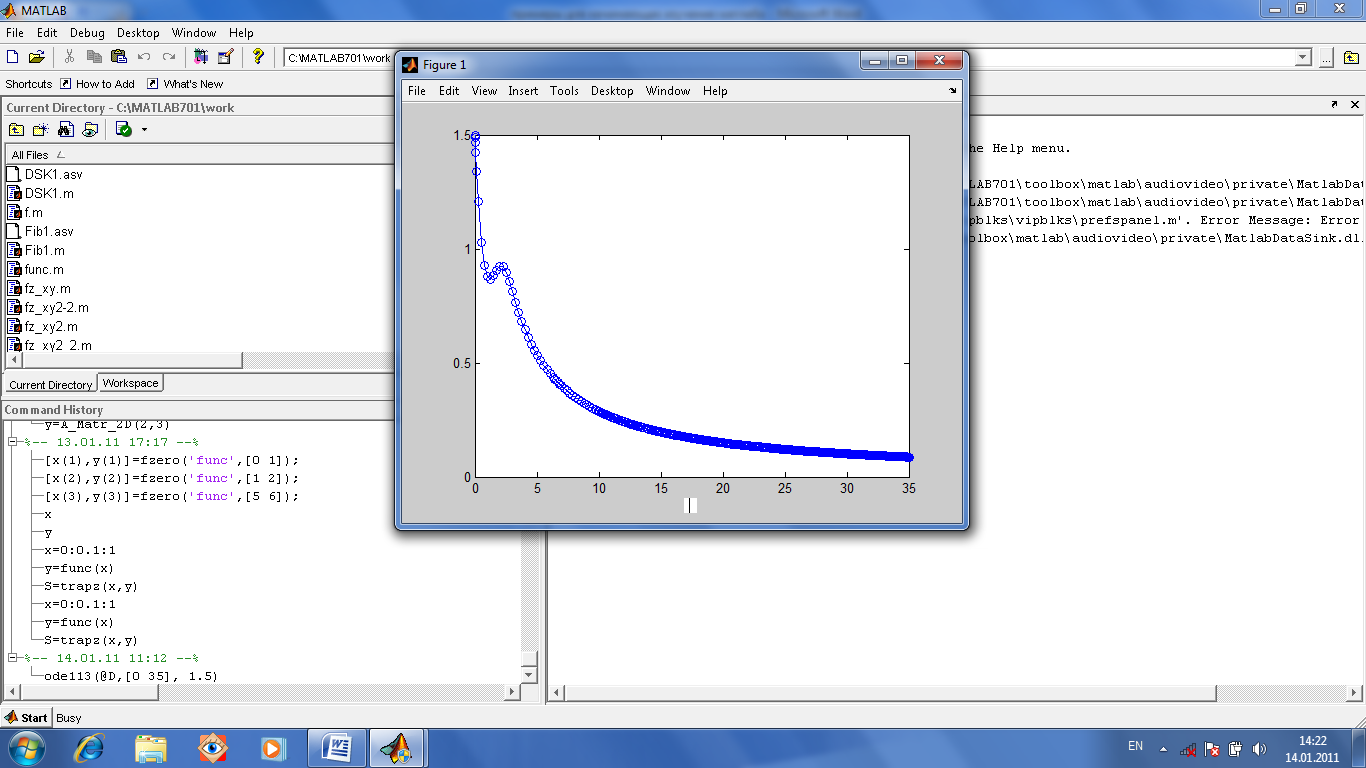
Решением системы является вектор x(t)=x1(t), x2(t), …,xn(t), который обращает вышеприведенные системы уравнений в тождества. Различают: задачу Коши, когда все дополнительные условия заданы в одной (чаще всего в начальной) точке интервала значений t; краевую задачу, когда дополнительные условия заданы на границах интервала значений t. Есть много встроенных функций, обеспечивающих решение вышеуказанных задач. Ниже описаны некоторые из них с примерами их использования. Входными параметрами этих функций являются: · f вектор-функция для вычисления правой части уравнения вида x’=f(x,t), удовлетворяющей начальному условию x(t0)=x0 или системы дифференциальных уравнений, данных в матричном виде dx/dt=f(t,x) с начальным условием x(t0)=x0 данным в матричном виде. · interval массив из двух чисел, определяющий интервал интегрирования дифференциального уравнения или системы. · X0 вектор начальных условий системы дифференциальных уравнений. · options параметры управления ходом решения дифференциального уравнения или системы уравнений. Все функции возвращают: · Массив Т содержащий координаты узлов сетки, в которых ищется решение. · Матрицу Х в которой i-й столбец является значением вектор-функции решения в узле Ti. Решим задачу Коши: dx/dt + x =sin xt при x(0)=1.5. Напишем М-функцию. Используем функцию ode113, которая реализует метод Адамса. Она строит график (рис.1.30) решения.
Рис.1.30. График решения дифференциального уравнения
В качестве ее параметров используются: @D ссылка на М-функцию, [0 35] интервал интегрирования уравнения, начальное условие x(0)=1.5 указано в виде 1,5 на соответствующем месте в списке параметров. Обращение к функции: ode113(@D, [0 35], 1.5). Решим систему дифференциальных уравнений на интервале [0 10] при
Напишем М-функцию syst.
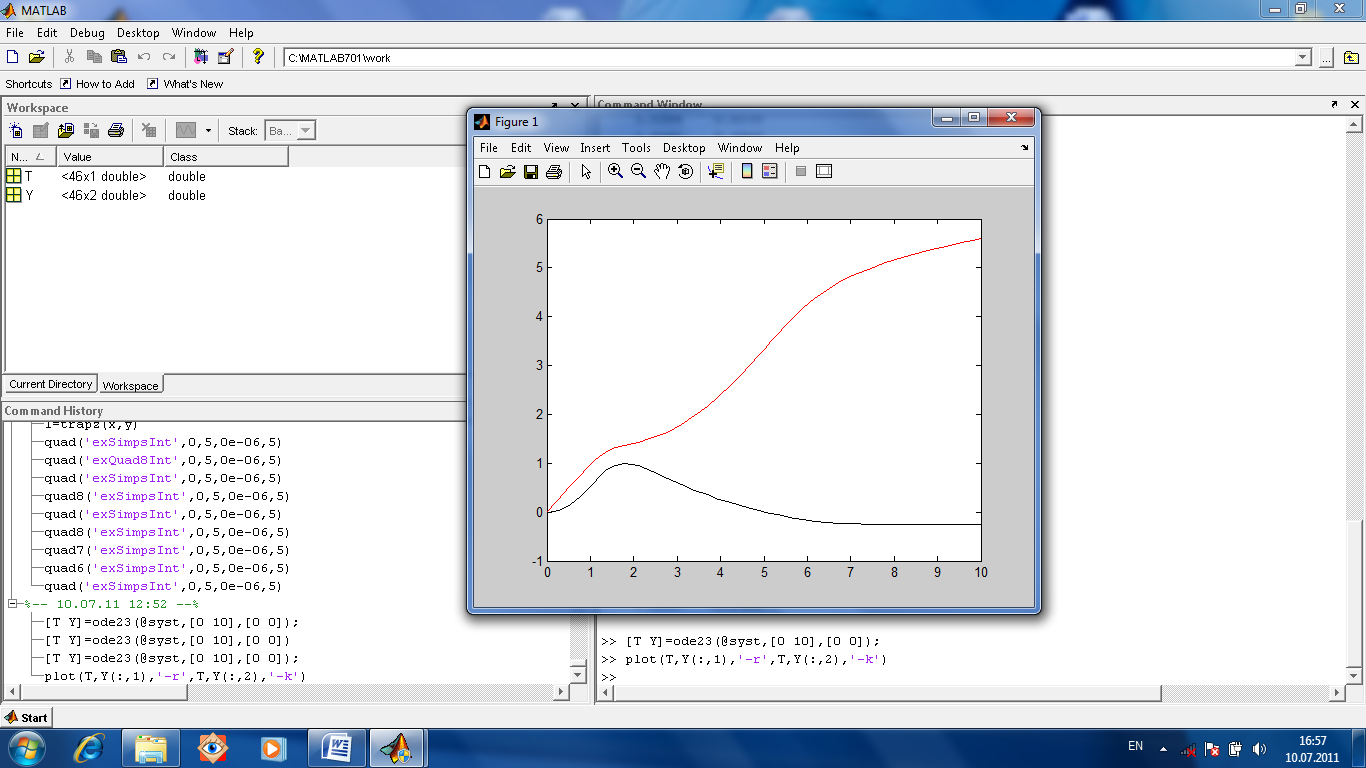
Используем функцию ode23 решающую методом Рунге-Кутта 2-3 порядка. Ее вызов [T, Y]=ode23(@syst, [0 10], [0 0]); где явно указаны выходные параметры вектор Т и матрица Y, а также указаны интервал [0 10] и начальные значения [0 0]. Затем формируем график решения plot(T,Y(:,1)’-r’,T,Y(:,2),’-k‘). Получаем (рис.1.31) график.
Рис.1.31. График решения системы дифференциальных уравнений. Решение жестких задач. Для решения жестких задач действуют в два этапа. Сначала убеждаются, что система жесткая (действительные части всех собственных чисел матрицы dx / dt = B отрицательны и величина s = max | Re (h)|/ min | Re (h)|, называемая числом жесткости системы, велика). После этого решают систему с помощью соответствующих функций матпакета. Найдем решение задачи Коши для следующей системы:
имеющей начальное условие X(0)=(1 1 1 1); Опишем систему в функции exSyst_1.
Сначала проверим, является ли матрица В матрицей жесткой системы. Оператор eig(B) возвращает собственные числа матрицы. Одно из них неотрицательное, то есть условие соблюдено не полностью. Далее находим число жесткости s=28, что не очень много, то есть система не очень жесткая. Затем команда ode15s решает задачу. Возвращается вектор Т и матрица Х, число столбцов в которой равно числу переменных. Строим график (рис.1.32). На нем видно, что корни изменяются в зависимости от параметра Т как бы синусоидально. Такой характер изменений корней характерен для жестких систем. По мере роста числа жесткости, корни колеблются (в зависимости от параметра Т) все более резко, образуя «детский рисунок» на экране.
Рис.1.32. График решения жесткой системы.
Решение дифференциальных уравнений высших порядков. Если в уравнении есть производные высших порядков, то действуем, преобразуя уравнение с понижением степени производной, но с увеличением числа переменных. Решим краевую задачу. d 2 x / dt 2 +4 dx / dt +13 x = esin t при x (0.25)=-1, x / (0.25)=1 на интервале [0.25; 2]. Преобразуем следующим образом. Пусть y=dx/dt. Тогда получим систему уравнений.
с начальными условиями y(0.25)=1, x(0.25)=-1; опишем ее в функции exSistVP.
Для ее решения воспользуемся функцией ode45.
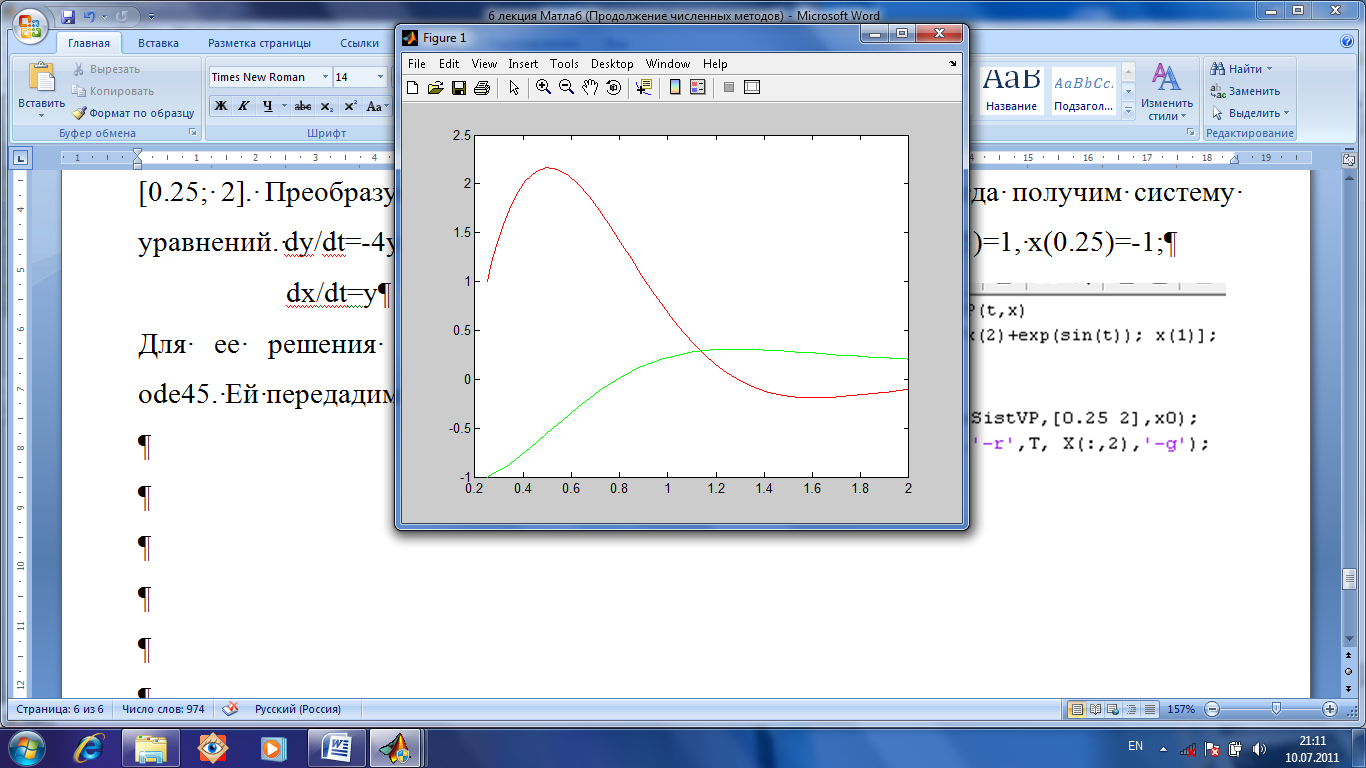
Функция ode45 вернет нам матрицу для Х и вектор для Т. Построим (рис.1.33) график.
Рис.1.33. Решение диф. уравнения высших порядков. Обработка результатов эксперимента. Построение полиномиальной зависимости. Для этого есть функция polyfit, которой передаются массив абсцисс, массив ординат (экспериментальных точек) и степень полинома, который требуется получить так, чтобы он описывал экспериментальную зависимость массива ординат от массива абсцисс. Функция возвращает вектор коэффициентов вышеупомянутого полинома.
Будет построен график (рис.1.34),на котором можно будет сравнить исходные точки и расчетный график. Расчетный график построен по коэффициентам полинома.
Рис.1.34. Данные эксперимента и расчетный график. Зная коэффициенты полинома, можно функцией polyval вычислить значение полинома при любом значении его аргумента (то есть получить сплошную расчетную кривую, проходящую через отдельно расположенные экспериментальные точки). Если же требуется подобрать такую зависимость, которая не содержит некоторые степени (например, y =3 x 5 +6 x 3 + x +65) то тем самым требуется найти минимум функции. Поясним это на примере. Пусть требуется функция вида y = c 1 + c 2 x 2 + c 3 x 3, тогда, используя функцию fminsearch (‘ fname ’, c) получим вектор коэффициентов. Однако в функцию fminsearch следует передавать не вышеописанную функцию у(х), а переделанный ее вариант вида yiexperimental -(c 1 + c 2 xi 2 + c 3 xi 3). Тогда минимум функции будет достигнут в случае, если вычисленные ее значения практически совпадают с экспериментальными, то есть идеально описывают экспериментальные данные. Опишем для этого функцию exGl.
Затем вводим экспериментальные данные. После этого запускаем функцию fminsearch. Полученный от нее вектор значений с используем для построения (рис.1.35) расчетной кривой. Потом сравниваем, насколько точно кривая идет через экспериментальные точки.
Рис.1.34. Расчетная кривая идет между экспериментальными точками.
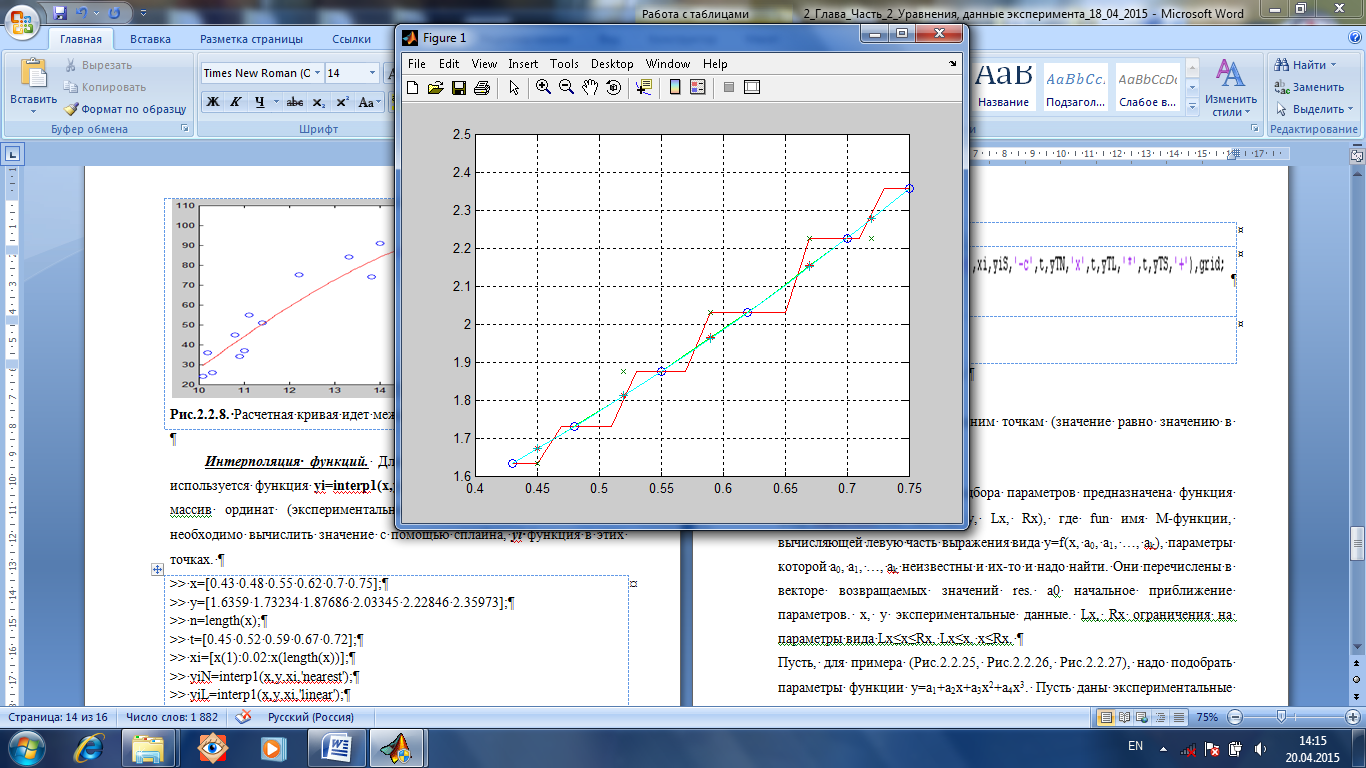
Интерполяция функций. Для реализации сплайн-интерполяции используется функция yi = interp 1(x, y, xi, method) где х массив абсцисс, у массив ординат (экспериментальных точек), xi точки, в которых необходимо вычислить значение с помощью сплайна, yi функция в этих точках. В зависимости от используемых методов, получаются различные результаты (Рис.1.36). Для уплотнения экспериментальных точек, создан массив xi из точек с одинаковым шагом, и для них будут найдены значения функции y(x). Кроме того, создан массив из точек t и эти точки расположены между экспериментальными. Для них тоже будут найдены значения функции y(t)
Рис.1.36. В зависимости от используемых методов, получаются различные расчетные результаты. function Start_interp1 x=[0.43 0.48 0.55 0.62 0.7 0.75]; y=[1.6359 1.73234 1.87686 2.03345 2.22846 2.35973]; n=length(x); t=[0.45 0.52 0.59 0.67 0.72]; xi=[x(1):0.02:x(length(x))]; yiN=interp1(x,y,xi,'nearest'); yiL=interp1(x,y,xi,'linear'); yiS=interp1(x,y,xi,'spline'); yTS=interp1(x,y,t,'spline'); yTN=interp1(x,y,t,'nearest'); yTL=interp1(x,y,t,'linear'); plot(x,y,'o',xi,yiN,'r-',xi,yiL,'g-',xi,yiS,'c-',t,yTN,'x',t,yTL,'*',t,yTS,'+'); grid on; end linear линейная интерполяция; spline кубический сплайн; nearest интерполяция по соседним точкам (значение равно значению в ближайшей узловой точке). Подбор параметров. Для подбора параметров предназначена функция [ res ]= lsqcurvefit (fun, a 0, x, y, Lx, Rx), где fun имя М-функции, вычисляющей левую часть выражения вида y = f (x, a 0, a 1, …, ak), параметры которой a 0, a 1, …, ak неизвестны и их-то и надо найти. Они перечислены в векторе возвращаемых значений res. а0 начальное приближение параметров. x, y экспериментальные данные. Lx, Rx ограничения на параметры вида Lx ≤ x ≤ Rx, Lx ≤ x, x ≤ Rx. Пусть, для примера (Рис.1.37), надо подобрать параметры функции y = a 1 + a 2 x + a 3 x 2 + a 4 x 3. Пусть даны экспериментальные данные.
Выберем вектор начальных приближений а0=(2, 0, 1,0). Опишем функцию exMnk, она вычисляет значение многочлена
Затем введем данные и построим график по ним.
Применим функцию lsqcurvefit(@exMNK,a0,x,y), получим коэффициенты полинома.
Рис.1.37. Экспериментальные данные и расчетный график. Поиск экстремума функции одной переменной. При решении задач поиска максимума (минимума) выделяют локальный (с указанием границ) и глобальный максимум (минимум). Поиск (локального (в пределах определенного интервала) минимума осуществляет функция [ x, y ]= fminbnd (имяФункции,границыИнтервала). Если же надо найти локальный максимум, то исследуемую функцию берут с другим знаком и ищут ее минимум, который фактически является ее максимумом. При этом значение функции в максимуме это найденное значение с другим знаком. Локальный минимум функции одной переменной ищет встроенная функция [x, y]=fminbnd(name, a, b, options). В ней: · name имя М-функции, · a, b границы поиска, · options параметры управляющие ходом решения, · x, y координаты точки минимума. Для вычисления локального максимума, надо взять функцию name с другим знаком. Для примера, рассмотрим функцию y(x)=x4-0.5x3-28x2+140 Сначала найдем минимум на интервале, например, от -4 до -2. [x,y]=fminbnd(@ext,-4,-2), где @ext обращение к М-функции вычисляющей интересующую нас функцию. Потом найдем максимум на интервале от -6 до 6, для этого обратимся не к @ext, а к @ext_2, в которой функция y(x) взята с другим знаком, то есть y(x)=-(x4-0.5x3-28x2+140). То есть ее минимум будет максимумом исходной функции. Получим и в том, и в другом случае координаты точки минимума (максимума) на заданном отрезке, что и требовалось.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 72; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.80.122 (0.038 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
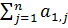 xj + b1
x2’=
xj + b1
x2’=  xj + b1
.…………………..
xn’=
xj + b1
.…………………..
xn’= 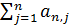 xj + b1
xj + b1