Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построим несколько графиков одновременноСодержание книги
Поиск на нашем сайте
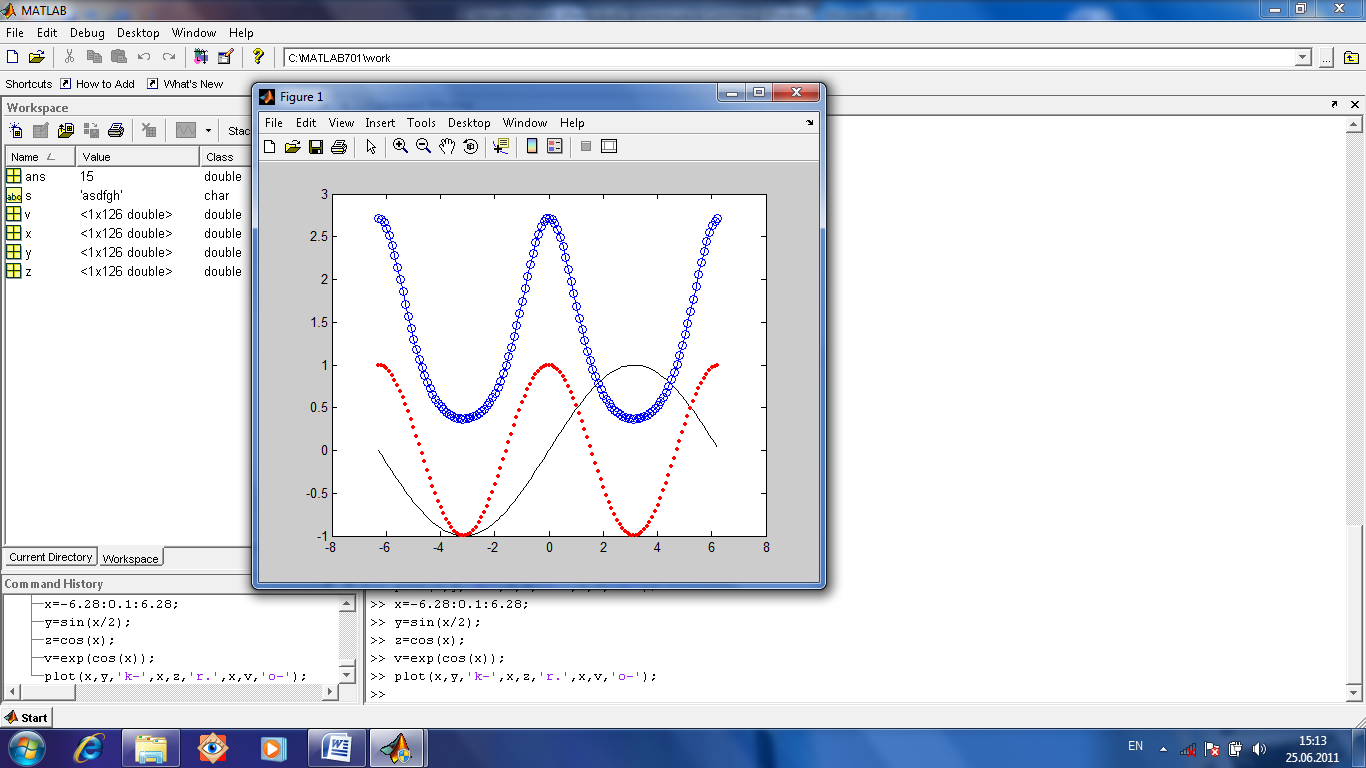
Для этого зададим массив х от -6,28 с шагом 0,1 до 6,28. x=-6.28:0.1:6.28;. Затем зададим функции y(x), z(x), v(x). y=sin(x/2); z=cos(x); v=exp(cos(x)); После этого введем в командной строке команду plot(x,y,'k-',x,z,'r.',x,v,'o-'); где каждой паре (горизонтальные координаты, вертикальные координаты) указан тип маркера и цвет линии (‘ r.’ красные точки без линии, ‘ o -‘ синие кружочки с линией). Кроме того, команда grid on наносит сетку на график, функция title (‘Заголовок’) выводит заголовок графика, функции xlabel (‘Подпись под осью Х’), ylabel (‘Подпись под осью У’) служат для подписи осей. (Рис.1.10)
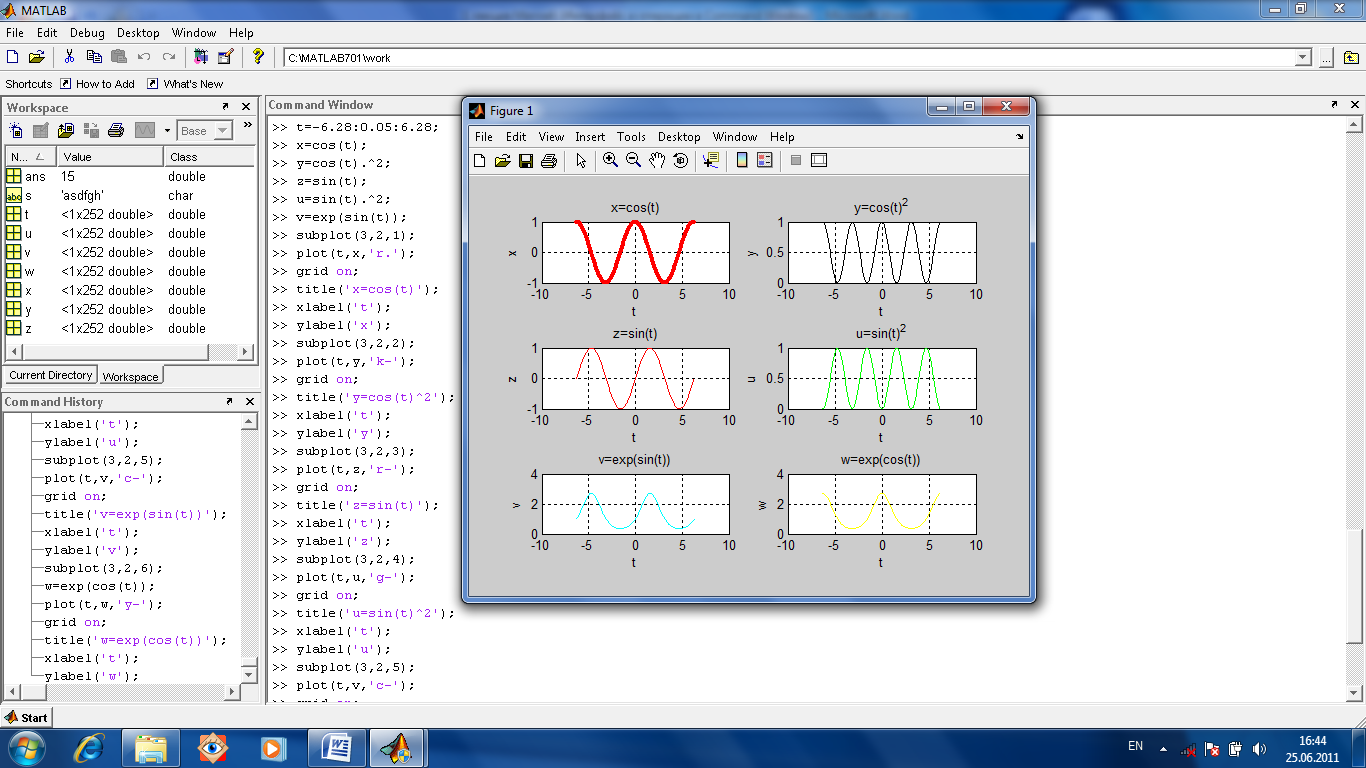
Рис.1.10.Несколько графиков одновременно. x =-6.28:0.1:6.28; y=sin(x/2); z=cos(x); v=exp(cos(x)); plot(x,y,'k-',x,z,'r.',x,v,'o-'); Построим несколько графиков отдельно друг от друга, но в одном окне (рис.1.11). Команда subplot(3,2,1); означает (Рис.1.11) что окно разбивается на три маленьких окна для построения графиков по вертикали, на две колонки таких окон по горизонтали, и начинаем описывать первый (левый верхний) из графиков. Аналогично последующие команды subplot отличаются только номером очередного графика. Текст (последовательность команд) введен в окне Command Window.
При описании функций, содержащих операции умножения и возведения в степень, надо учитывать, что их аргумент является массивом чисел. Соответственно, функция тоже будет получена в виде массива. Его элементы будут результатом поэлементного обращения функции к массиву аргумента. Поэтому ставится знак «точка» при описании функции y=cos(t).^2; или u=sin(t).^2; знак «точка» ставится после аргумента, перед знаком операции возведения в степень.
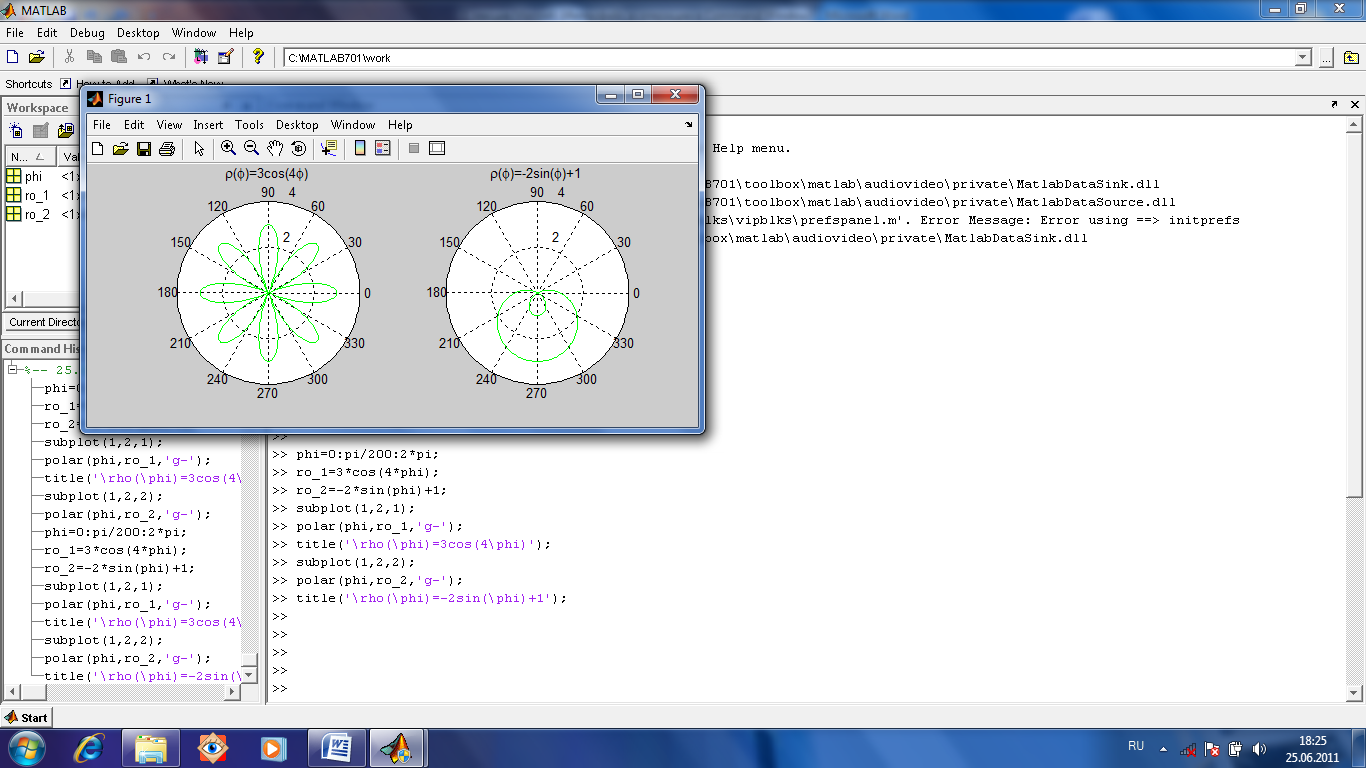
Рис.1.11.Несколько графиков отдельно друг от друга, но в одном окне. Построим график в полярной системе координат (рис.1.12). Для этого сформируем массив значений полярного угла phi и полярного радиуса ro и используем команду polar(phi, ro, s), где s строка из трех символов, задающих цвет линии, тип маркера и тип линии. Можно ограничиться только цветом и типом линии. В МАТЛАБе предусмотрена автозамена комбинаций латинских букв на греческие буквы. Так например \phi заменяется на ϕ, \rho заменяется на ρ. Поэтому в команде title(‘Заголовок’) указываем в заголовке не греческие буквы а соответствующие им комбинации латинских букв. На рис.1.12 показан график.
Рис.1.12. График в полярной системе координат
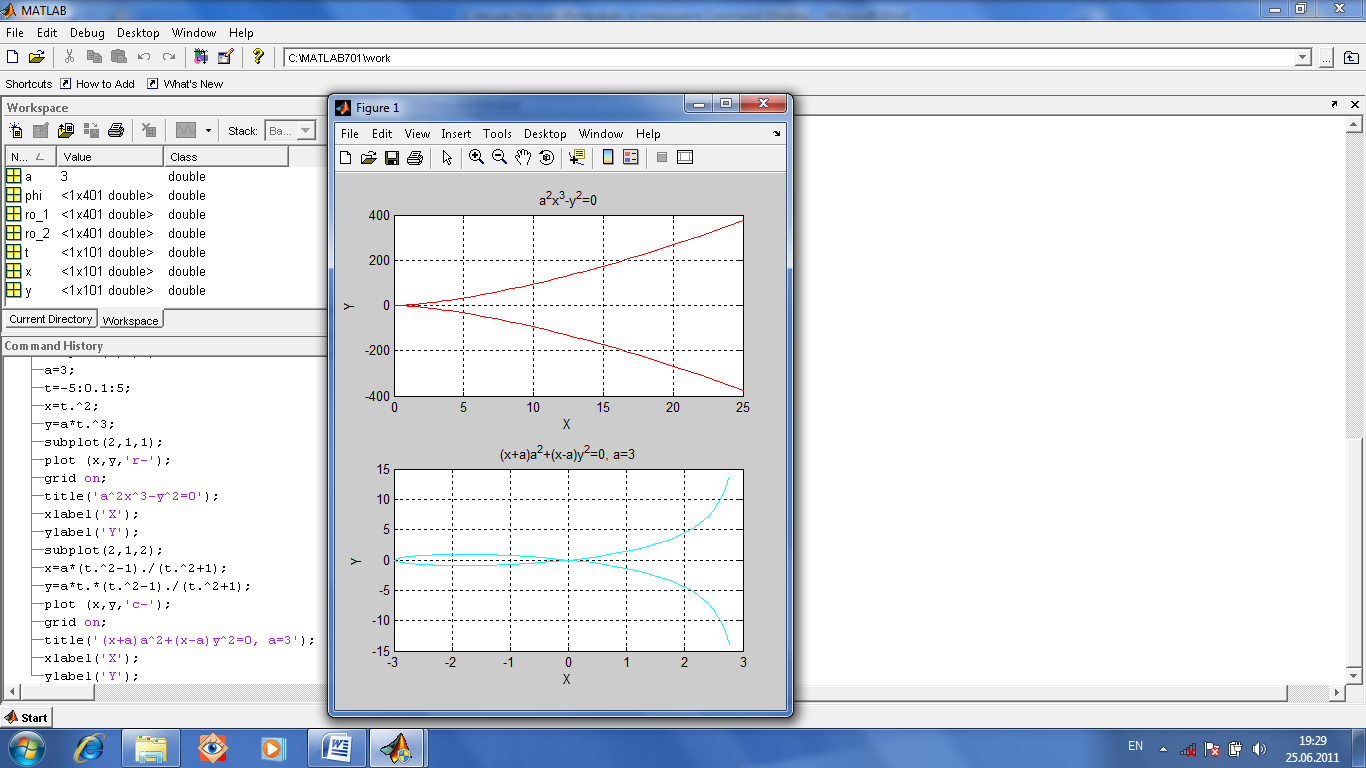
phi=0:pi/200:2*pi; ro_1=3*cos(4*phi); ro_2=-2*sin(phi)+1; subplot(1,2,1); polar(phi,ro_2,'g-'); title('\rho(\phi)=-2sin(\phi)+1'); subplot(1,2,2) polar(phi,ro_1,'g-'); title('\rho(\phi)=3*cos(4*(\phi))'); Построим график функции, заданной в параметрической форме (рис.1.13). Для этого определим массив параметра t. Затем определим массивы функций от параметра. Пусть x=f(t), y=g(t). Затем построим график функции у(х) с помощью команды plot(x,y). Построим график a2x3-y2=0 (a>0). Параметрическое представление таково: x=t2, y=at3, -∞<t<∞. Пусть а=3. Рядом построим график (x+a)a2+(x-a)y2=0, a>0. Параметрическое представление таково: x(t)=a(t2-1)/(t2+1), y(t)=at(t2-1)/(t2+1)
Рис.1.13. График функции, заданной в параметрической форме
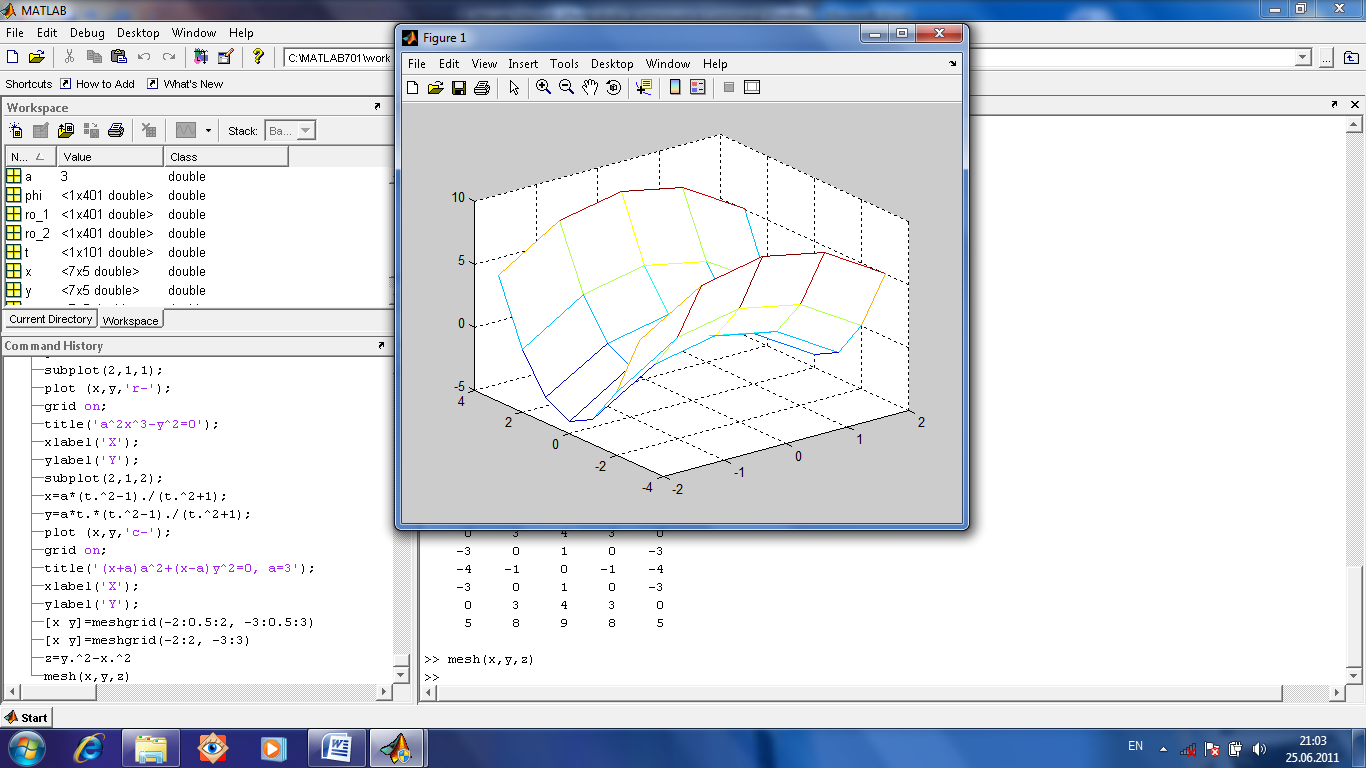
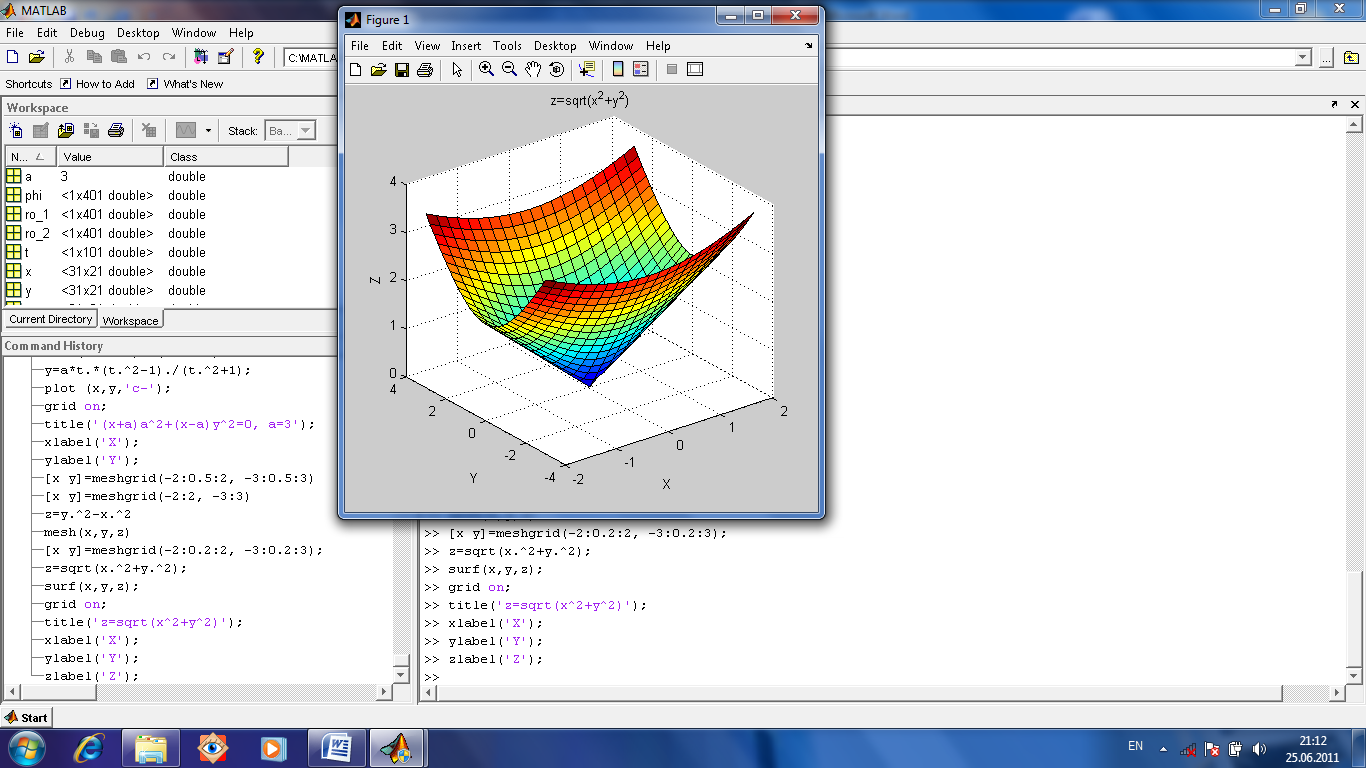
В МАТЛАБе графики можно модифицировать, используя возможности графического окна, в котором они отображаются. Для этого с помощью инструмента «стрелка» выделяется элемент, а затем щелчками кнопок мыши открываются соответствующие списки действий или пункты меню. Команда File-Generate M-file позволяет автоматически сгенерировать файл с программой, строящей именно такой график. Ее можно сохранить, нажав на сохранение. Построим трехмерный график z(x,y) (рис.1.14). Для этого необходимо по каждой из двух переменных x и y создать массив двумерный. Например x=-2:2 и y=-3: 3. Массивы создаются командой [ x y ]= meshgrid (-2:2, -3:3)
Рис.1.14. Трехмерный график z(x,y) построен командой mesh(x,y,z) Кроме того, есть еще функция для построения поверхности (Рис.1.15), покрашенной в соответствии со значениями z(x,y).
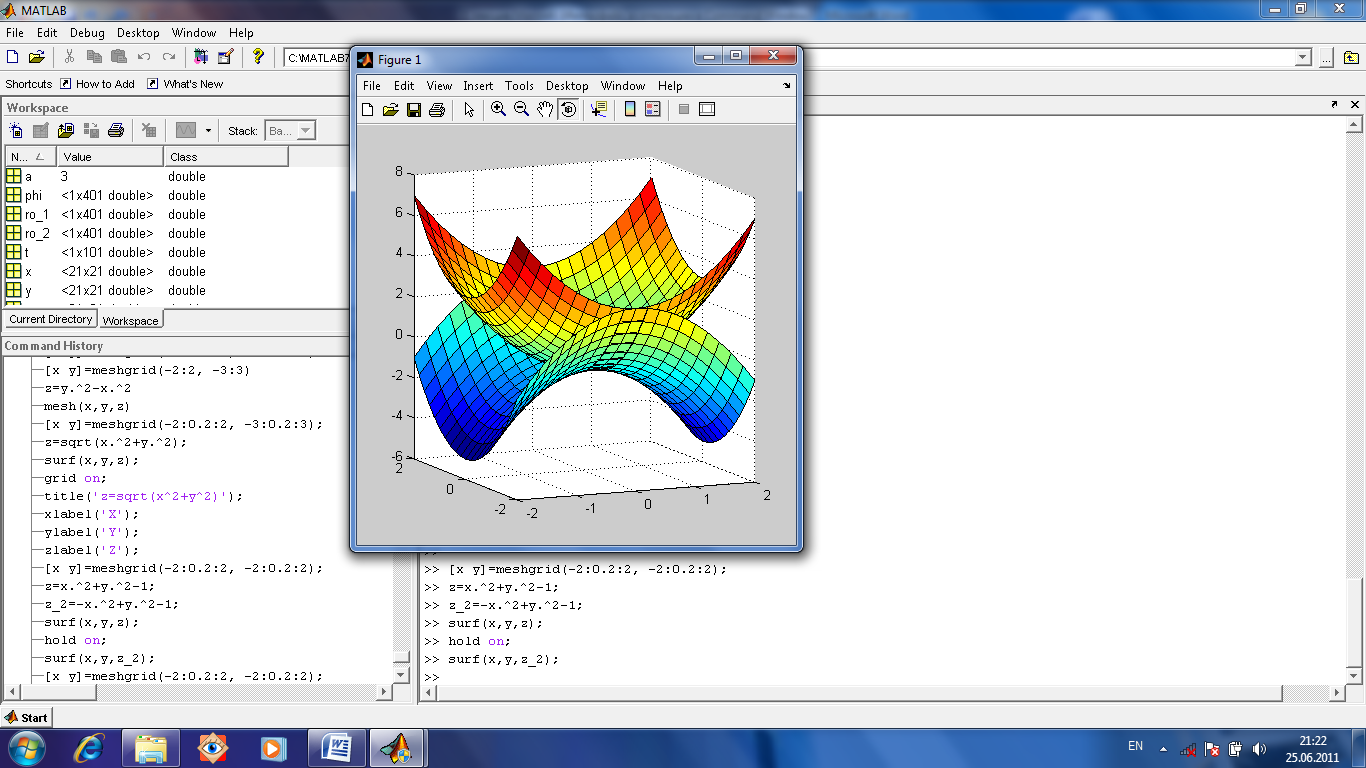
Рис.1.15. Трехмерный график построен командой surf(x,y,z) Похоже на географическую карту с окраской по высоте изображенных участков местности. Для нее тоже строим сетку функцией meshgrid, затем находим значения (массив значений) z(x,y) и тогда уже вызываем surf (x, y, z). Трехмерную фигуру можно повернуть любой стороной и рассмотреть поудобней. Для этого в окне фигуры надо ткнуть кнопку Rotate3D и можно мышкой зацепить и повертеть фигуру. Построить две трехмерные фигуры в одном окне (рис.1.16). Используется команда hold on которая вынуждает МАТЛАБ построить новую трехмерную поверхность в прежнем окне. Для нее тоже строим сетку функцией meshgrid, затем находим значения (массив значений) z(x,y) и тогда уже вызываем surf(x,y,z).
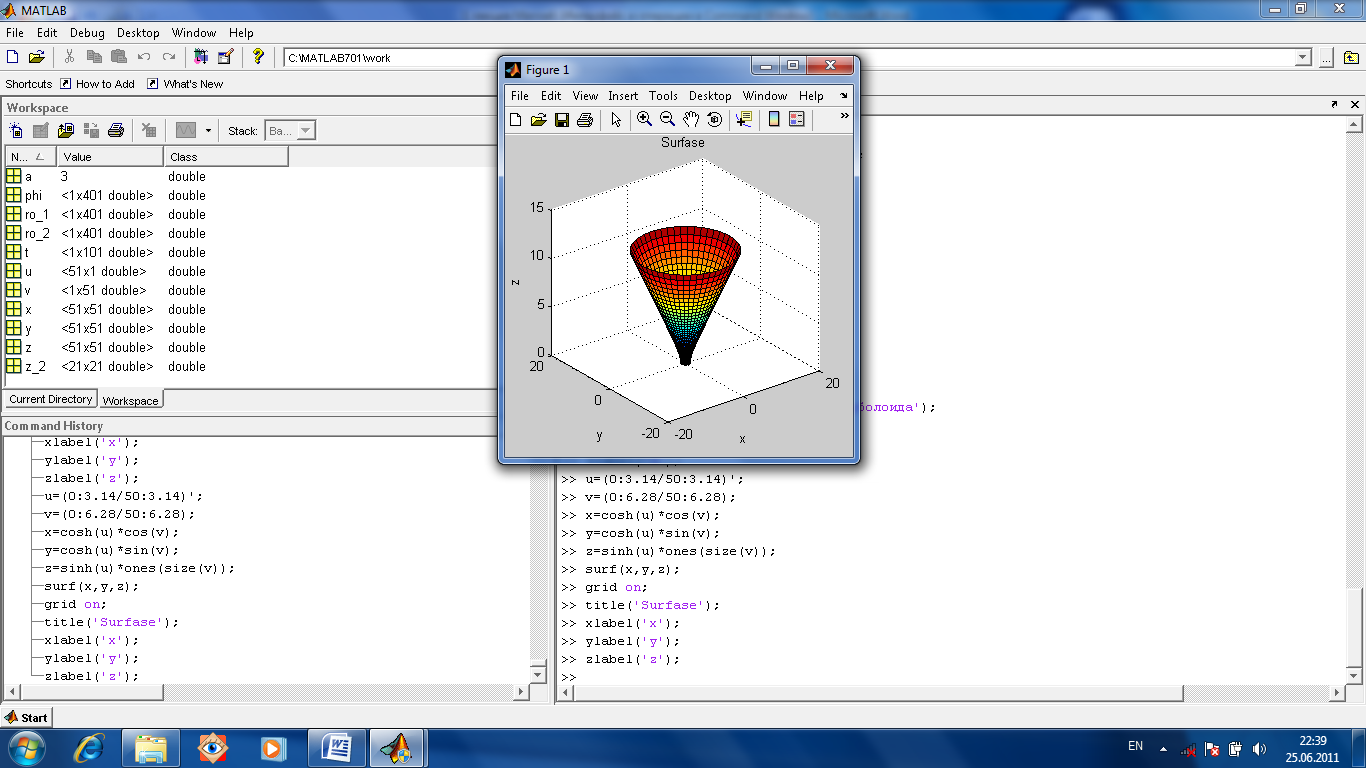
Рис.1.16. Трехмерный график построен двумя командами surf(x,y,z) >>[x y]=meshgrid(-2:0.2:2, -2:0.2:2); >> z=x.^2+y.^2-1; >> z_2=-x.^2+y.^2-1; >> surf(x,y,z); >> hold on; >> surf(x,y,z_2); Построим поверхность заданную параметрически (рис.1.17). Пусть х(u,v)=ch(u)cos(v), y(u,v)=ch(u)sin(v), z(u,v)=sh(u).
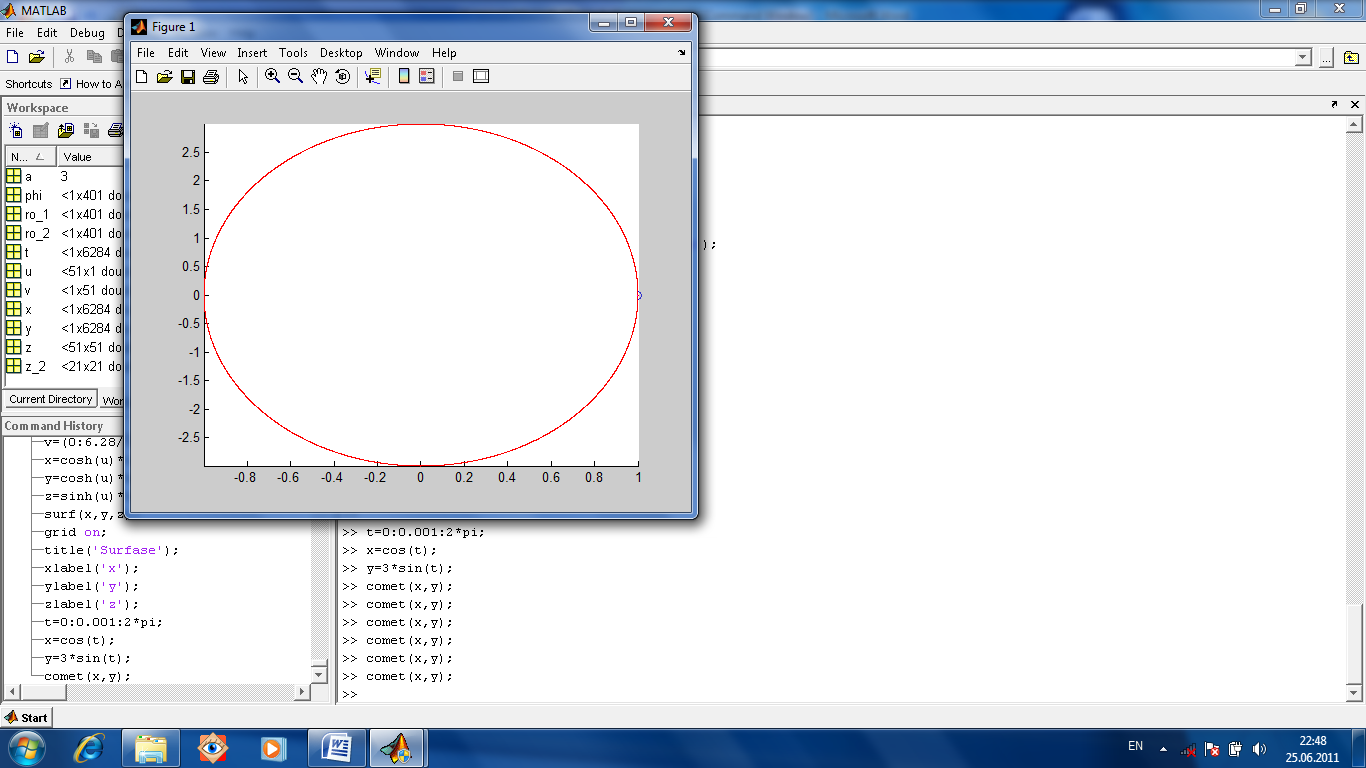
Рис.1.17. Поверхность заданная параметрически. Построим сначала для параметра u вектор-столбец u=(0:3.14/50:3.14)’; знак ’ означает транспонирование. Затем для второго параметра v построим вектор-строку с таким же количеством (это важно!) элементов v=(0:2*3.14/50:6.28); Формируем для x(u,v) матрицу как матричное произведение столбца ch(u) и строки cos(v) то есть x=cosh(u)*cos(v) где cosh это косинус гиперболический на языке операторов МАТЛАБа. Аналогично y=cosh(u)*sin(v); После этого надо сформировать матрицу z как матричное произведение столбца sh(u) на строку единиц такой же длины. Для построения строки единиц такой же длины используем команду ones(size(v)); Таким образом z=sinh(u)*ones(size(v)); Затем формируем график поверхности surf(x,y,z); u=(0:3.14/50:3.14)'; v=(0:6.28/50:6.28); x=cosh(u)*cos(v); y=cosh(u)*sin(v); z=sinh(u)*ones(size(v)); surf(x,y,z); grid on; title('Surface'); xlabel('x'); ylabel('y'); zlabel('z'); Построим график движения точки на плоскости (рис.1.18). Пусть она движется по кривой заданной параметрически. х(t)=cos(t), y(t)=3sin(t). Используем оператор comet(x,y). Он позволяет анимировать движение точки.
Рис.1.18. График движения точки на плоскости t=0:0.001:2*pi; x=cos(t); y=3*sin(t); comet(x,y); Движение точки вдоль винтовой линии заданной параметрически (рис.1.19). Пусть x(t)=sin(t), y(t)=cos(t), z(t)= t, можно смоделировать с помощью команды comet3(sin(t),cos(t),t); t=0:pi/500:10*pi; comet3(sin(t),cos(t),t);
Рис.1.19. График движения точки вдоль винтовой линии, заданной параметрически. Настройки графиков
Форматирование текста
Форматирование символов
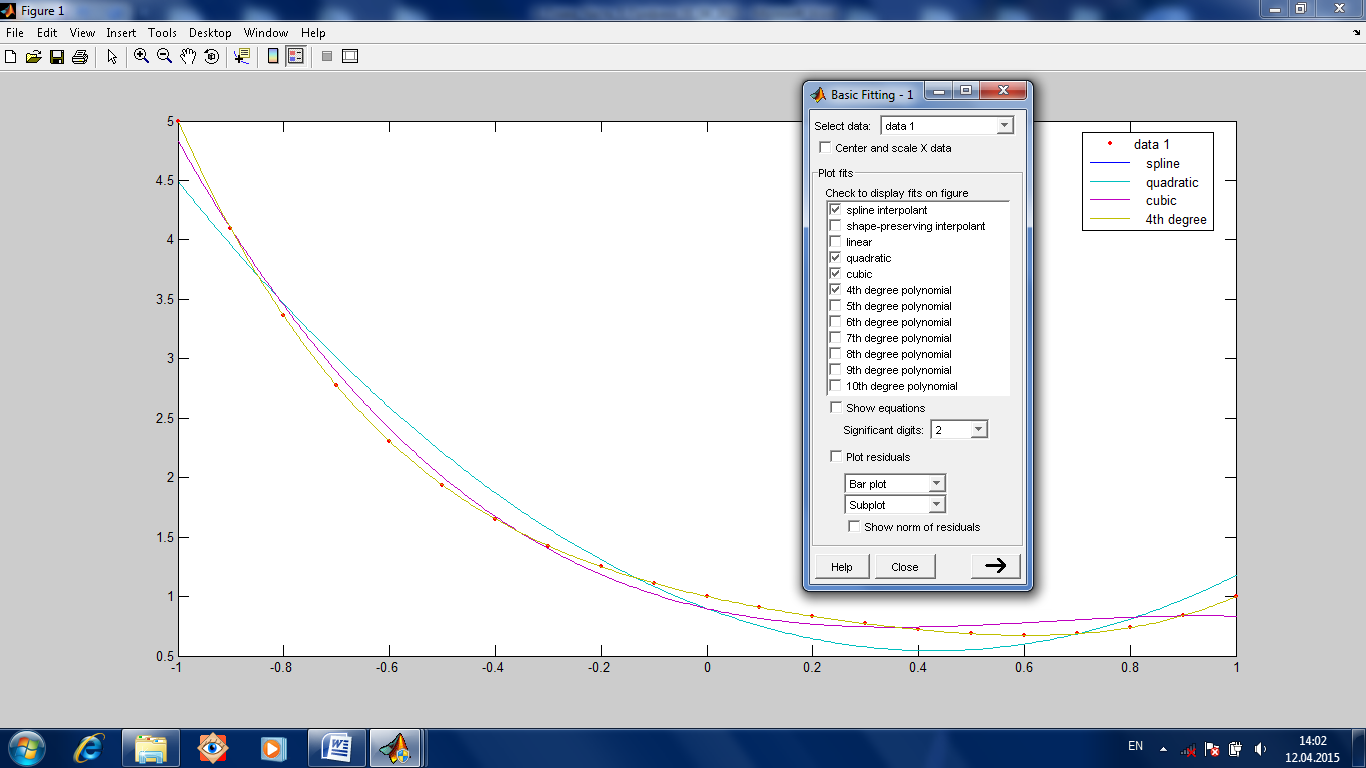
На рис.1.20 показан процесс подбора уравнения, график которого наиболее близок к тому, который построен по желанию пользователя Пусть мы хотим построить график функции y=x.^4-x.^3+x.^2-x+1 при х от -1 до 1 с шагом 0,1. Затем откроем в меню Tools, в раскрывающемся списке команд, команду Basic Fitting и выберем интересующие нас варианты функций.
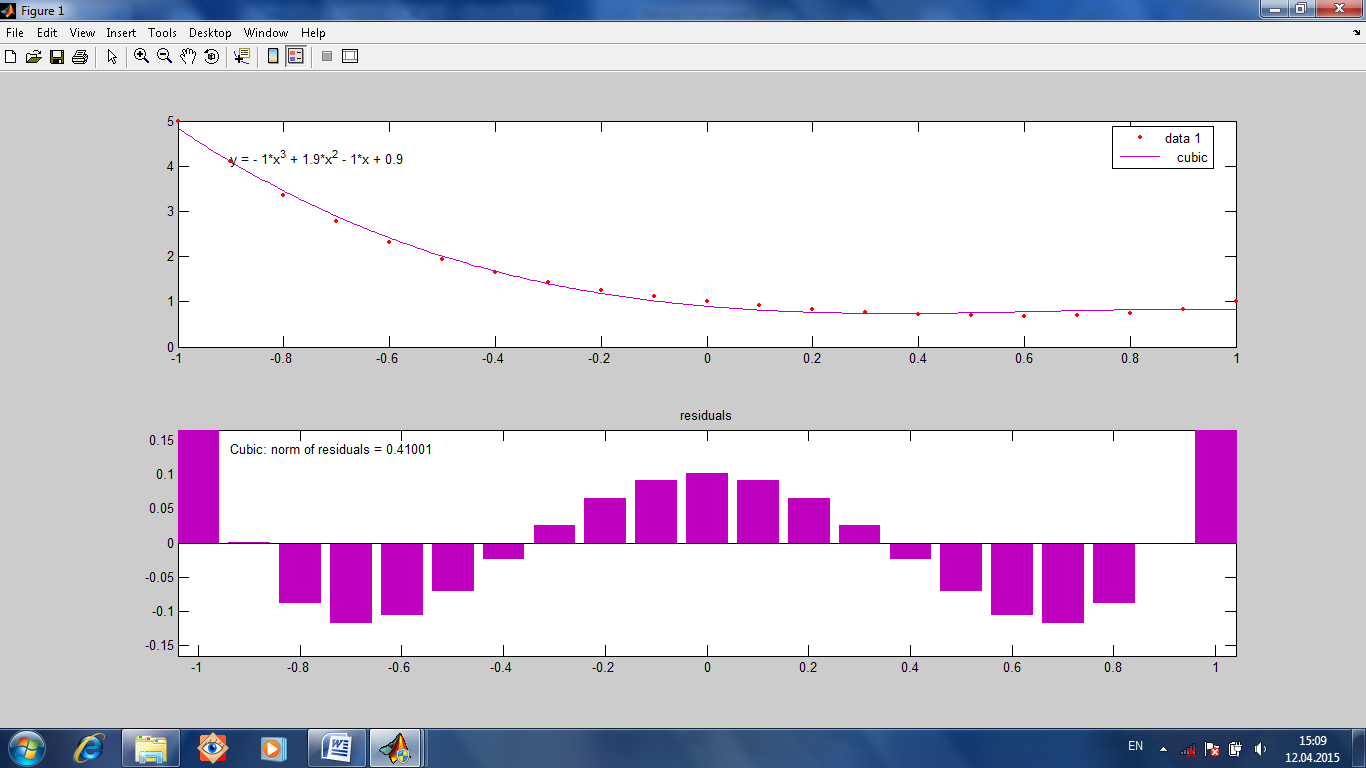
Рис.1.20. Меню Basic Fitting с выбранными (поставлены галочки) функциями, графики функций и легенда к ним. Исходные точки, заданные пользователем, в легенде подписаны как data 1. Также можно оценить степень совпадения графика функции, выбранной в Basic Fitting, с исходным графиком. Для этого надо выбрать Plot residuals в меню Basic Fitting. Для вывода корня из суммы квадратов погрешностей, надо выбрать Show norm of residuals. Также можно вывести уравнение функции на экран. Для этого в меню Basic Fitting надо выбрать Show equiations (Рис.1.21).
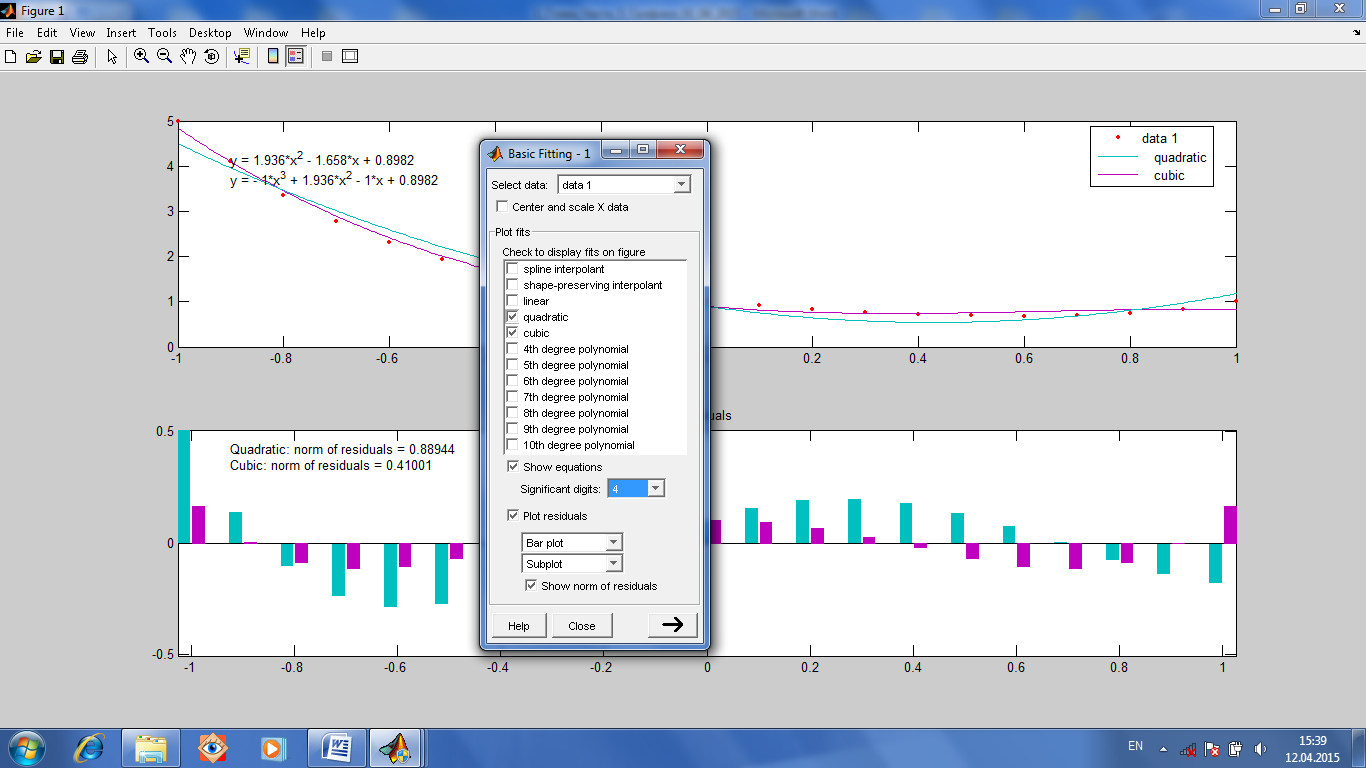
Рис.1.21. Наверху график полинома третьей степени и его уравнение, точки-исходные данные, внизу отклонения между графиком полинома и исходными точками, норма отклонений. Можно выбрать несколько разных графиков. Тогда будут одновременно отображаться несколько уравнений и несколько погрешностей. Можно выбрать количество цифр (Significant digits) в уравнениях на экране (рис.1.22).
Рис.1.22. Несколько графиков одновременно, их уравнения и погрешности относительно исходных данных.
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 298; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.199.240 (0.007 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||

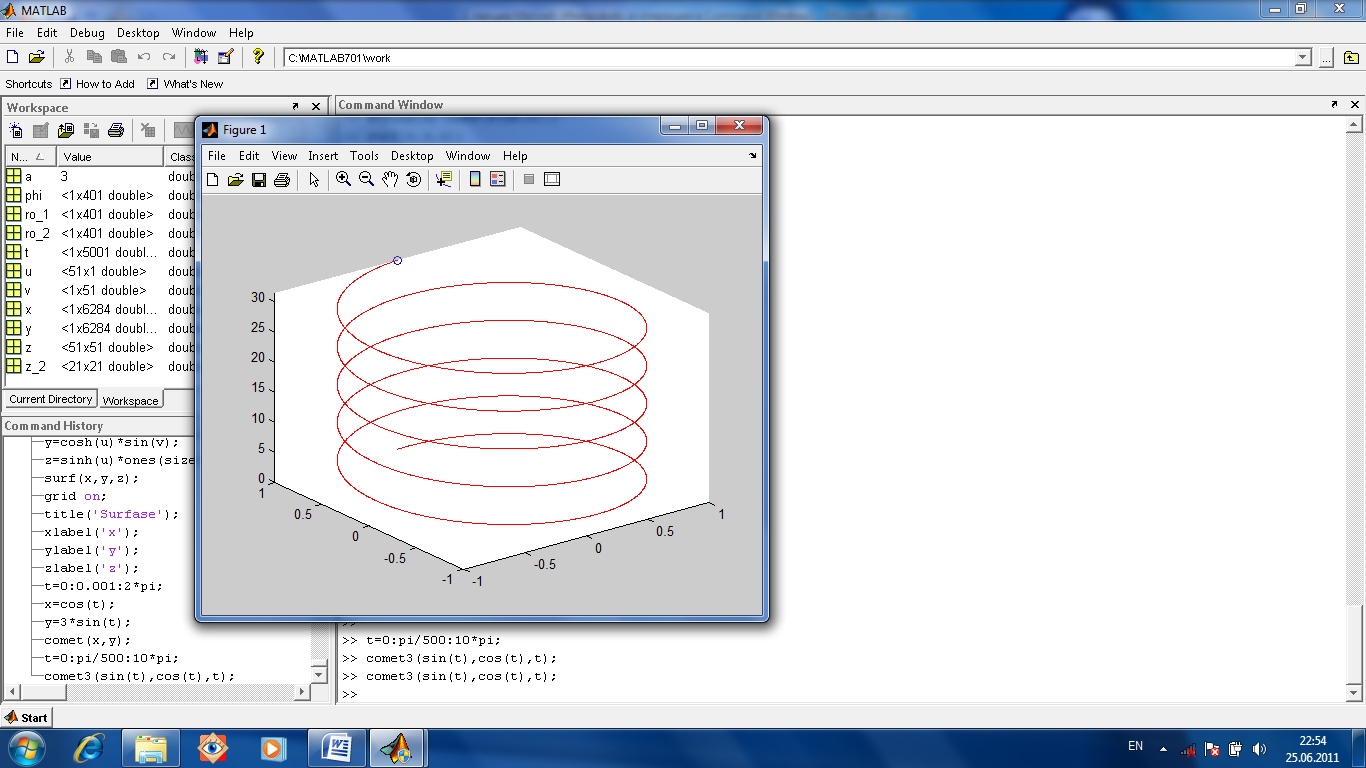
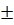 \geq ≥
\inftyo ∞
\partial ∂
\neq ≠
\nabla
\geq ≥
\inftyo ∞
\partial ∂
\neq ≠
\nabla 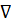 \forall
\forall 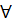 \exists
\exists 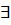 \approx ≈
\in
\approx ≈
\in 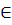 \sim ~
\leq ≤
\leftrightarrow ↔
\leftarrow ←
\uparrow ↑
\rightarrow →
\downarrow ↓
\circ °
\sim ~
\leq ≤
\leftrightarrow ↔
\leftarrow ←
\uparrow ↑
\rightarrow →
\downarrow ↓
\circ °