
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Источники и классификация погрешностей результатаСодержание книги
Поиск на нашем сайте
Получить точное значение при решении задачи на машине практически невозможно. Получаемое решение всегда содержит погрешность и является приближенным. Источники погрешности: Погрешность математической модели определяется выбором математической модели. Погрешность в исходных данных определяется: погрешностью измерения или погрешностью вычислений, с помощью которых они были получены. Погрешность численного метода определяется точностью выбранного числено метода и вычислительного средства. Абсолютная и относительная погрешности. Пусть α* — точное (и никогда неизвестное) значение некоторой величины, а α — известное приближение к нему, то абсолютной погрешностью приближенного значения α называется величина: Относительной погрешностью приближенного значения α называется величина: Значащими цифрами числа называют все цифры в его записи, начиная с первой ненулевой слева. Например, в числах α = 0.0 3045, α = 0.0 304500 значащими цифрами являются подчеркнутые цифры. Число значащих цифр в первом случае равно 4, во втором 6. Значащую цифру называют верной в широком смысле, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего этой цифре или верной в узком смысле, если абсолютная погрешность числа не превосходит половины единицы разряда, соответствующего этой цифре. Примеры: α = 0.0304500. Верные цифры подчеркнуты (Табл.2.2.1).
Табл.2.2.1. Верные цифры в числе в широком и узком смысле. Правила округления известны. Обратить внимание, что если первая из отброшенных цифр равна 5 и все остальные отброшенные цифры являются нулями, то последняя оставшаяся цифра остается неизменной, если она четная (правило четной цифры), и увеличивается на единицу, если она нечетная. При этом погрешность не превышает пяти единиц отброшенного разряда. Пример: 6.71 - 6.7; 6.77 - 6.8; 6.75 - 6.8; 6.65 - 6.6 Особенности машинной арифметики В ЭВМ происходит отбрасывание или усечение. В некоторых языках программирования реализованы общепринятые правила округления. Вещественные числа в ЭВМ представляются (Табл.2.2.2) в экспоненциальном виде (с плавающей точкой):
Табл.2.2.2. Примеры записи чисел. Если представить мантиссу в виде m = 0.d1 d2 d3 d4...... dk, то при d1≠0 получаем нормализованную форму числа, где к – количество цифр в мантиссе, называют разрядной сеткой (Табл.2.2.3). Примеры: 0.512 * 104 разр.сетка = 3; 0.5200 * 104 разр.сетка = 4 Если к = 3 то, следующие числа представим как:
Табл.2.2.3. Нормализованная форма числа. В последних двух примерах цифры, выходящие за разрядную сетку отброшены. При этом погрешность округления не превышает единицы последнего оставленного разряда. Выполнение операций над вещественными числами начинается и заканчивается выравниванием порядков. Если порядки различны – погрешность возрастает и может привести к потере точности. По возможности надо избегать работать с числами, порядки которых отличаются на величину, близкую к длине разрядной сетки, а также вычитания близких по значению величин Сложить слева направо и наоборот следующие числа: 0.522·100, 0.157·10-1, 0.186·10-1, 0.239·10-1
Погрешности вычислений Абсолютная погрешность суммы или разности нескольких чисел не превосходит суммы абсолютных погрешностей этих чисел.
Относительная погрешность суммы: Относительная погрешность разности: Относительная погрешность произведения Относительная погрешность частного: Абсолютная погрешность дифференцируемой функции многих переменных:
Пример. Для заданной функции: Вычисляем значение функции. Вычисляем погрешности:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 120; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.205.21 (0.008 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

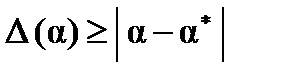
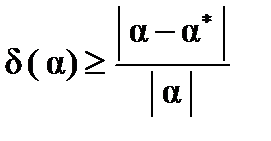
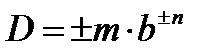 где m – мантисса, b – основание системы счисления, n - порядок. В десятичной системе счисления:
где m – мантисса, b – основание системы счисления, n - порядок. В десятичной системе счисления: 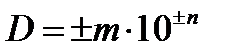
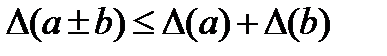
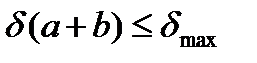
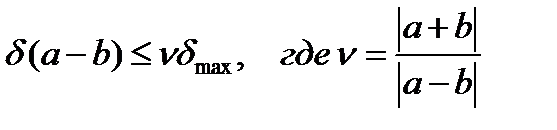
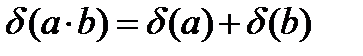
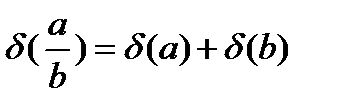
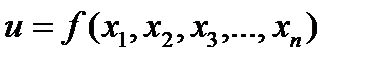
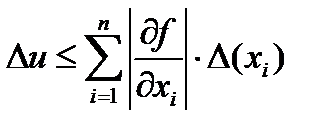
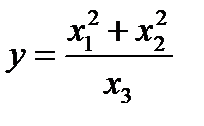 определить y,
определить y, 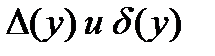 при x1= -1.5, x2= 1.0, x3= 2.0. Все цифры в данных верные для x1 в широком смысле, а для x2 и x3 в узком смысле.
при x1= -1.5, x2= 1.0, x3= 2.0. Все цифры в данных верные для x1 в широком смысле, а для x2 и x3 в узком смысле.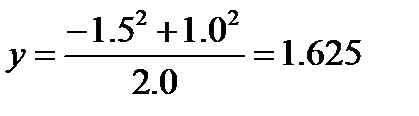
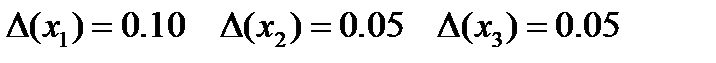
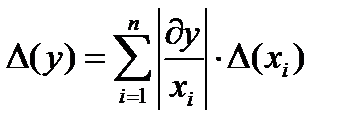 тогда
тогда 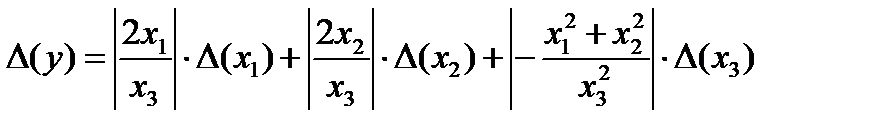 или
или 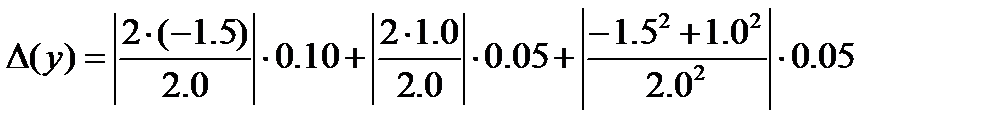 следовательно
следовательно 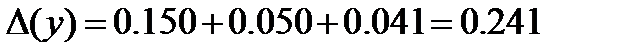 Отсюда получаем
Отсюда получаем 



