
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Учет инфляции и налогов при начислении процентов
Во всех рассмотренных выше случаях мы не учитывали влияние на параметры сделки инфляции и налогов. В условиях реального снижения покупательной способности денег рассмотрим механизмы этого влияния на результаты финансовых операций. Инфляция Инфляция характеризуется обесцениванием национальной валюты (т. е. снижением ее покупательной способности) и общим повышением цен в стране. Очевидно, что в различных случаях влияние инфляционного процесса сказывается на договаривающихся сторонах неодинаково: когда кредитор теряет часть дохода за счет обесценивания денежных средств, дебитор получает возможность выиграть на том, что может погасить долг деньгами меньшей покупательной способности. Инфляцию необходимо учитывать при расчете наращенной и текущей сумм денег, а также при определении доходности какой-либо финансовой операции. Пусть S – наращенная сумма денег, измеренная по номиналу, S Отношение При расчетах используют относительную величину уровня инфляции – темп инфляции a, причем
Тогда для определения S Величину (Индекс инфляции Jи называют еще индексом цен.) Например, если уровень инфляции равен 50 %, то цены выросли в полтора раза. В свою очередь, Напомним, что изменение покупательной способности денег за некоторый период измеряется с помощью индекса Jпс, который равен обратной величине индекса инфляции:
При этом Следует отметить, что индексы Jи и Jпс относятся к одному и тому же временному интервалу. Пусть в настоящий момент получено 100 тыс. руб. и известно, что за два предшествующих года цены увеличились в два раза, т. е.
Динамика индекса инфляции за некоторый период отражает изменения в экономических процессах за это время. Понятно, что повышение индекса инфляции за определенный период, по сравнению с предыдущим таким же периодом, указывает на ускорение инфляции (и, соответственно, на снижение покупательской способности), снижение – на уменьшение ее темпов. Среднегодовые темпы роста цен iи и уровень инфляции Н находятся из величины Jи: Если Н – прогнозируемый уровень инфляции за период, то за n периодов имеем: Наиболее часто встречающаяся (грубая) ошибка в финансово-экономических расчетах – это простое суммирование темпов инфляции для получения обобщающего показателя за весь период. Например, пусть цены каждый месяц растут на 4 %. Тогда за годовой уровень инфляции принимают величину 12´4=48 %. Такие расчеты часто используют банки и финансовые компании, привлекая клиентов вкладывать средства, к примеру, под 60 % годовых. Между тем, если уровень инфляции составляет 4 % в месяц, то это означает, что за месяц цены вырастут в 1+0,04=1,04 раза, а за год – в 1,0412=1,665 раза. Значит, годовой индекс инфляции составляет 1,665-1=0,665, т. е. годовой уровень инфляции составляет 66,5 %. После такого расчета процентная ставка в В общем виде индекс цен за несколько неодинаковых периодов равен произведению индексов цен цепочки периодов: Это означает, что цены в текущем периоде повышаются на Нt процентов относительно уровня, сложившегося в предыдущем периоде. ПРИМЕР 2.15 Постоянный темп инфляции имеет уровень: а) 3 % в месяц; б). имеет место последовательный прирост цен по месяцам: 5, 4 и 3 %. Найти годовой уровень инфляции и темп инфляции за 3 месяца. РЕШЕНИЕ. а) по формуле (2.43) найдем индекс цен
Тогда годовой уровень инфляции вычисляем по формуле (2.42):
б) Индекс цен за три месяца, согласно формуле (2.44), равен: 1,05 ´ 1,04 ´ 1,03=1,1248. Тогда уровень инфляции за 3 месяца составит 1,1248-1=0,1248, т. е. 12,48 %. Рассмотрим, до какой же степени могут обесцениться деньги при операции наращения. Последнее, как обычно, производится по простой и сложной ставке процентов. Если взять простую ставку, то, подставляя соответствующий множитель наращения в формулу (2.41), получим
Из (2.45) видно, что реальное увеличение суммы будет иногда, когда множитель наращения простых процентов будет больше, чем индекс инфляции. Если наращение производится по сложной ставке процентов, то, подставив в (2.41) значение S и Jи, найдем:
Согласно (2.45) и (2.46), множители наращения с учетом инфляции для простых и сложных процентов будут:
Проанализируем, при каких соотношениях между i и
Если Для простых процентов минимально допустимую процентную ставку найдем, приравнивая единице множитель наращения (2.54 а)): 1+ it =(1+
При данной процентной ставке наращение по простым процентам будет полностью компенсировать инфляцию. ПРИМЕР 2.16 Пусть на сумму 150 тыс. руб. в течение трех месяцев начисляются простые проценты по ставке 50 % годовых. Найти наращенную сумму с учетом обесценивания и минимально допустимую величину ставки, если индекс цен за 3 месяца составляет 1,1250 (пример 2.15). РЕШЕНИЕ. По формуле (2.52.)
Таким образом, только ставка, превышающая 80 % годовых, будет в данных условиях приносить реальный доход. Естественно, для того чтобы компенсировать обесценивание денег, необходимо произвести индексирование процентной ставки, т. е. увеличить ее на некоторую величину. Последняя называется инфляционной премией, а сумма ставки и инфляционной премии называется в литературе «брутто-ставкой». Найти ее можно, приравняв соответствующие множители наращения. Так, если i – простая ставка, а τ – брутто ставка, то
1+ τ ´ n =(1+in)Jи=(1+ in)(1+
Отсюда τ = Если i – ставка сложных процентов, то из равенства (1+ τ) n =(1+ i) n (1+ 1+ τ =(1+ i)(1+ следует, что τ= i+ Выражение (2.55) представляет собой известную формулу И. Фишера. По этой формуле инфляционная премия, которую нужно прибавить к реальной ставке доходности для компенсации инфляционных потерь, равна величине (
τ = Следует понимать, что замена (2.49) на (2.50) оправдана лишь в случае незначительных величин Аналогично тому, как были получены формулы (2.48) и (2.49) находится выражение, связывающие учетные ставки. В случае простых учетных ставок соответствующее уравнение эквивалентности имеет вид:
откуда учетная ставка с учетом инфляции d Для случая сложных учетных ставок: Если начисление процентов происходит m раз в году, то
Отсюда а для сложных учетных ставок с m начислениями в году Решим теперь обратную задачу: найти реальную ставку процентов, учитывающую доходность операции, с учетом инфляции. Для этого нужно, используя вышеприведенные формулы, найти процентную ставку, если задана брутто-ставка τ. Если начисляются простые проценты, то из формулы (2.54) можно получить выражение, позволяющее определить реальную доходность финансовой операции, если задан уровень инфляции: Из формулы τ = получим аналогичную формулу для случая сложных процентов: Подставив в (2.57) значение индекса инфляции отражающую несколько очевидных соображений: - если - если - если
Имеет место еще один метод компенсации инфляции, при котором индексируется не процентная ставка, а первоначальная сумма платежа P. Тогда Величина P в нужные моменты времени корректируется с помощью индекса инфляции Jи. Данный метод распространен в Великобритании. Рассмотрим примеры учета инфляционных процессов.
ПРИМЕР 2.17 Ссуда в 50 тыс. руб. выдана на 2 года. Реальная доходность операции должна составить 20 % годовых по сложной ставке ссудных процентов. Ожидаемый уровень инфляции составляет 50 % в год. Определить множитель наращения, сложную ставку процентов, учитывающую инфляцию, и наращенную сумму. РЕШЕНИЕ По формуле (2.50) получаем:
Отсюда множитель наращения
Для наращенной суммы будем иметь
ПРИМЕР 2.18 Первоначальный капитал в размере 20 тыс. руб. выдан на 3 года с процентами, начисленными в конце каждого квартала по номинальной ставке 30 % годовых. Определить номинальную ставку процентов и наращенную сумму с учетом инфляции, если годовой ожидаемый уровень инфляции составляет 40 %. РЕШЕНИЕ. Воспользуемся формулой (2.50): Jn=(1+0,4)3=3,8416. По формуле (2.59) имеем:
Отсюда
ПРИМЕР 2.19 При выдаче кредита должна быть обеспечена реальная доходность операции, определяемая учетной ставкой 20 % годовых. Кредит выдается на полгода, за которые предполагаемый индекс инфляции составит 1,4. Рассчитать значение учетной ставки, компенсирующей потери от инфляции. РЕШЕНИЕ. Произведем вычисления по формуле
ПРИМЕР 2.20. Определить реальную доходность финансовой операции, если при уровне инфляции 4 % в месяц выдается кредит на 2 года по номинальной ставке сложных процентов 80 % годовых. Проценты начисляются ежеквартально. РЕШЕНИЕ. Принимая заданную номинальную процентную ставку за ставку, учитывающую инфляцию, получим:
j= ПРИМЕР 2.21 Определить, какой реальной убыточностью обладает финансовая операция, если при уровне инфляции 40 % в год капитал вкладывается на один год под номинальную ставку 25 % годовых при ежемесячном начислении. РЕШЕНИЕ. Используем для расчета формулу (2.66) при Jи=1,4:
Таким образом, данная операция будет приносить 6 %-й убыток. Учет налогов Очень часто прибыль от финансовой операции определяется полностью начисленными за какой-то срок процентами. Эта прибыль (или полученные проценты) облагается налогом, сумма которого уменьшает наращенное значение денег. Рассмотрим, как влияет налог на полученные проценты, на результаты финансовой операции. Пусть g –ставка налога на проценты, S, как и прежде – наращенное значение без учета выплаты налога, Sg – та же сумма с учетом налога. Пусть начисляются простые проценты. Тогда
Sg=S-I×g=S-(S-P)g=S-Sg+Pg=S(1-g)+Pg=P(1+ni)(1-g)-Pg=P(1+n(1-g)i). (2.62)
Из формулы (2.62) видно, что учет налога эквивалентен сокращению процентной ставки i на (1+ g). Рассмотрим случай начисления сложных процентов. Если налог начисляется на срок n, то его сумма равна величине
а наращенная сумма окажется Налог может начисляться в конце каждого периода, например года. Тогда проценты постоянно увеличиваются. В литературе по финансовому анализу приводится формула для начисления налога за t -й год: ПРИМЕР 2.22 Пусть ставка налога на проценты равна 10 %. Ссуда, размером 100 тыс. руб., выдана на срок 3 года под 30 % годовых. Определить наращенную сумму с учетом налогов при начислении: а) простых процентов, б) сложных процентов. РЕШЕНИЕ а) Наращенная сумма на весь срок, 3 года, без уплаты налогов будет равна S =100(1+0,33)=190,0 тыс. руб.
|
||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 466; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.121.131 (0.078 с.) |
 – эта же сумма с учетом инфляции. Тогда
– эта же сумма с учетом инфляции. Тогда 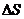 будет обозначать разницу между этими суммами.
будет обозначать разницу между этими суммами.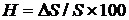 , выраженное в процентах, называется уровнем инфляции.
, выраженное в процентах, называется уровнем инфляции. .
. . (2.38)
. (2.38)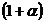 , показывающую, во сколько раз S
, показывающую, во сколько раз S 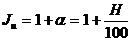 . (2.39)
. (2.39)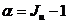 ,
,  . (2.40)
. (2.40)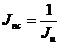 .
.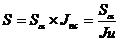 . (2.41)
. (2.41)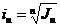 ; Н=
; Н= 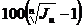 . (2.42)
. (2.42)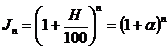 . (2.43)
. (2.43)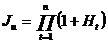 . (2.44)
. (2.44)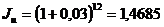 .
.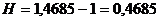 , т.е. 46,85%, а не 12*0,03=0,36, т.е. 36 %.
, т.е. 46,85%, а не 12*0,03=0,36, т.е. 36 %.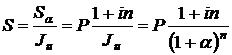 . (2.45)
. (2.45)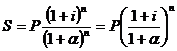 . (2.46)
. (2.46)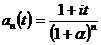 ;
; 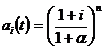 . (2.47 а), (2.47 б)
. (2.47 а), (2.47 б)
 > i, будет «эрозия» капитала (рис. 2.7),
> i, будет «эрозия» капитала (рис. 2.7),  при
при 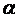 , называется ставкой процента.
, называется ставкой процента.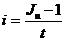 .
.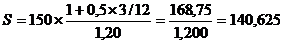 тыс. руб.
тыс. руб.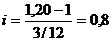 или 80 % годовых.
или 80 % годовых.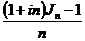 . (2.48)
. (2.48)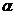 )
)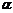 и i. При увеличении последних ошибка при отбрасывании последнего числа в (2.49) может быть весьма ощутимой. Так, при
и i. При увеличении последних ошибка при отбрасывании последнего числа в (2.49) может быть весьма ощутимой. Так, при  ,
,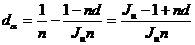 . (2.51)
. (2.51)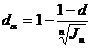 . (2.52)
. (2.52)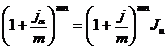 .
.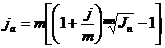 , (2.53)
, (2.53)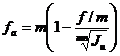 . (2.54)
. (2.54) . (2.55)
. (2.55)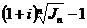 (2.56)
(2.56)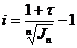 . (2.57)
. (2.57)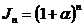 , получим простую формулу
, получим простую формулу , (2.58)
, (2.58)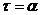 (доходность вложений и темп инфляции равны), то i =0, т. е. весь доход поглощается инфляцией;
(доходность вложений и темп инфляции равны), то i =0, т. е. весь доход поглощается инфляцией;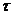 <
<  . (2.60)
. (2.60)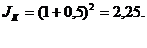
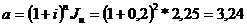 .
.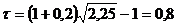 ,т. е.
,т. е.  тыс. руб.
тыс. руб.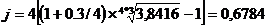 ; j=67,84 %.
; j=67,84 %.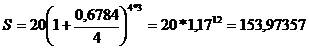 тыс. руб.
тыс. руб.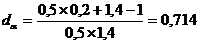 , т.е. d
, т.е. d 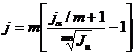 . (2.61)
. (2.61)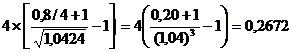 или 26,7 %.
или 26,7 %.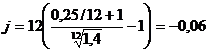 или -6 %.
или -6 %.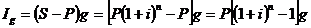 ,
,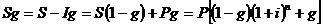 . (2.63)
. (2.63)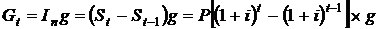 . (2.64)
. (2.64)


