
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непрерывное начисление процентов
До сих пор мы рассматривали только случаи дискретного начисления процентов. В банковской практике особенно при электронных способах регистрации финансовых операций, проценты могут начисляться за одни сутки или несколько часов. Например, коммерческий банк Москвы переводит банку Владивостока определенную сумму денег на 12 часов – с 20 часов сегодняшнего дня до 8 утра следующего дня по московскому времени. За счет разницы во времени банк г. Владивостока может использовать эту сумму в краткосрочных операциях, а затем вернуть долг с некоторым процентом к началу работы московского банка. Очевидно, что здесь присутствует задача начисления процентов за очень малые промежутки времени. По существу, речь идет о непрерывном начислении процентов. Аналогичные задачи могут возникнуть при анализе инвестиций, поскольку многие производственные и экономические процессы непрерывны по своей природе. Построим соответствующую им модель непрерывного начисления процентов. Рассмотрим такой пример. Найдем наращенное за 1 год значение на единицу основного капитала по ставке 100 % годовых с начислением m раз в году. Вычислим годовой множитель наращения. Результаты приведены в табл. 2.2. Таблица 2.2
Видно, что наращенная сумма увеличивается с ростом m, но как бы часто ни начислялись проценты, они не превысят числа 2,72= При непрерывном начислении процентов применяется особый вид процентной ставки, которая называется силой роста и обозначается Величина Наращенная сумма S:
Эффективная годовая ставка i и номинальная годовая ставка
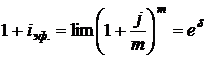 . (2.19) . (2.19)
Из формулы (2.19) следует, что
Формулами (2.19) и (2.20) пользуются при решении задач на непрерывное начисление процентов. Можно найти и приблизительную связь между основными параметрами. Из теории рядов известно, что при малых X с точностью до членов третьего порядка малости
Подставим первую из этих формул в (2.19), а вторую – в (2.20) и пренебрежем членами третьего порядка малости:
Этими приближенными формулами можно пользоваться для ориентировочных расчетов, если под руками нет калькулятора и таблиц. ПРИМЕР 2.9 Какой выигрыш получит инвестор за 2 года от вложения 200 тыс. руб. по ставке 8 % годовых, если вместо поквартального начисления процентов на эту сумму будут начислены непрерывные проценты? РЕШЕНИЕ. Обозначим через S1 наращенное значение при поквартальном начислении процентов, а через S2 – при непрерывном. Тогда
значит, выигрыш равен
Элементарно находится и дисконтный множитель на основе силы роста. Из (2.18) получим
Отсюда дисконтный множитель при непрерывном начислении процентов равен
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 234; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.133.96 (0.004 с.) |

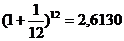
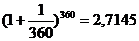
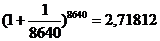
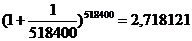
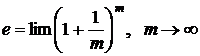 .
.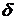 . Сила роста характеризует относительный прирост наращенной суммы за бесконечно малый промежуток времени и равна
. Сила роста характеризует относительный прирост наращенной суммы за бесконечно малый промежуток времени и равна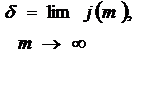 (2.17)
(2.17) называется также интенсивностью наращения за год при непрерывном начислении процентов.
называется также интенсивностью наращения за год при непрерывном начислении процентов.
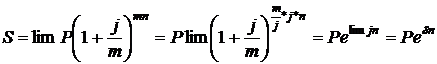 . (2.18)
. (2.18)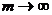
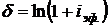 . (2.20)
. (2.20)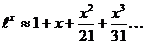
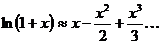
 ,
,  . 1)
. 1)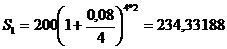 тыс. руб.
тыс. руб. тыс. руб.
тыс. руб.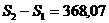 руб.
руб.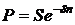 .
.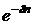 .
.


