
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: Применение дифференциальных уравнений при решении задач.
Краткое изложение темы. Уравнение, содержащее производные не выше второго порядка, называется дифференциальным уравнением второго порядка. В общем виде уравнение второго порядка записывается следующим образом:
Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида
где Алгоритм решения линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами:
а) Общее решение дифференциального уравнения выражается в виде
где б) Общее решение дифференциального уравнения выражается в виде
где в) Общее решение дифференциального уравнения выражается в виде
где
Примеры выполнения заданий. Пример 1. Решить уравнение Решение: Составим характеристическое уравнение:
Найдем корни данного уравнения:
Так как корни характеристического уравнения действительные и различные, то общее решение дифференциального уравнения запишется так:
Ответ: Пример 2. Решить уравнение Решение: Составим характеристическое уравнение:
Найдем его корни:
Здесь Так как характеристическое уравнение имеет два комплексно-сопряженных корня, то общее решение дифференциального уравнения записывается в виде
Ответ: Пример 3. Найти частное решение уравнения Решение: Составим характеристическое уравнение
Найдем его корни
Так как корни действительные и равны, то общее решение данного дифференциального уравнения записывается в виде
Продифференцируем общее решение
Подставив начальные данные в выражения для
откуда Следовательно, искомое частное решение имеет вид
Ответ: Пример 4. Найти частное решение уравнения Решение: Составим характеристическое уравнение
Найдем его корни
Так как корни комплексно-сопряженные, то общее решение данного дифференциального уравнения записывается в виде
Продифференцируем общее решение
Подставив начальные данные в выражения для
откуда Следовательно, искомое частное решение имеет вид Ответ: Пример 5. Найти закон движения тела по оси Ох, если оно начало двигаться из точки М (4;0) со скоростью v=2 t+3 t2. Решение: При прямолинейном движении скорость есть производная от пути по времени. Обозначив путь через х, имеем Проинтегрировав, получим х = t2 + t3 + C. Используя начальные условия найдем С. Так как х=4 при t=0, то, подставив эти значения в общее решение, находим С=4. Итак, закон движения тела имеет вид х = t2 + t3 + 4. Ответ: х = t2 + t3 + 4. Задания для практической работы. Вариант 1. 1. Решите уравнение: 2. Решите уравнение: 3. Найти частное решение дифференциального уравнения 4. Найти частное решение дифференциального уравнения 5. Найти закон движения тела по оси Ох, если оно начало двигаться из точки М (3;0) со скоростью v=4 t+3 t2.
Практическая работа № 11.
|
|||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 102; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.101.60 (0.022 с.) |
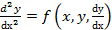 .
.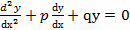 ,
,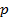 и
и 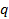 - постоянные величины.
- постоянные величины.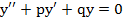 .
.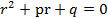 (если
(если 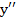 обозначить через
обозначить через 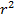 ,
, 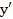 - через
- через 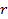 ,
, 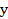 - через 1).
- через 1).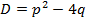 ; при этом если:
; при этом если: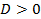 , то характеристическое уравнение имеет два разных корня
, то характеристическое уравнение имеет два разных корня 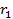 и
и 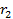 .
.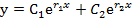 ,
, и
и 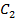 - произвольные постоянные.
- произвольные постоянные.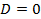 , то при этом характеристическое уравнение имеет два равных корня
, то при этом характеристическое уравнение имеет два равных корня 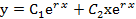 ,
,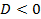 , то при этом характеристическое уравнение имеет комплексные корни
, то при этом характеристическое уравнение имеет комплексные корни 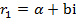 и
и 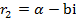 .
.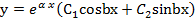 ,
,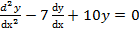 .
.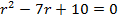 .
.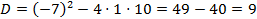 .
.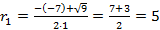 ,
,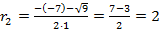 .
.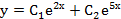 .
.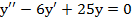 .
.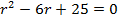 .
.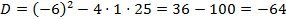 .
.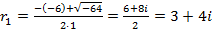 ,
,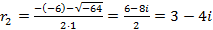 .
.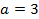 ,
, 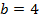 .
. .
.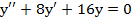 , если
, если 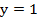 и
и 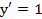 при
при 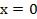 .
.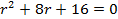
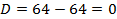
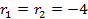
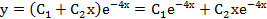
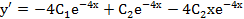 .
.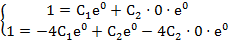
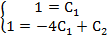 ,
,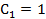 и
и 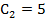 .
.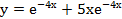 .
.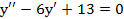 , если
, если 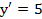 при
при 
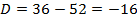
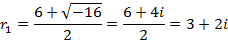
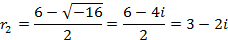
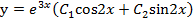 .
.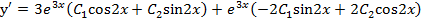
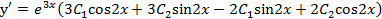
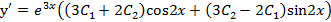 .
.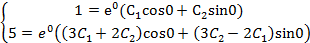
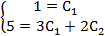 ,
,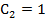 .
.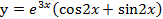 .
.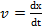 ; тогда
; тогда 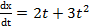 , или
, или  .
.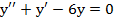 .
.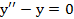 .
.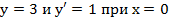 .
.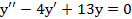 , если
, если 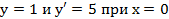 .
.


