
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: действия над матрицами.Стр 1 из 8Следующая ⇒
Практическая работа № 1. Тема: Действия над матрицами. Краткое изложение темы. Прямоугольная таблица чисел вида Числа, составляющие матрицу, называются элементами матрицы. Элементы матрицы образуют столбцы и строки. Здесь Произведение Произведением матрицы А на действительное число Суммой матриц A и В одинакового размера называется матрица С того же размера, каждый элемент которой равен сумме соответствующих элементов матриц А и В. Разность двух матриц одинакового размера определяется равенством: Произведением матриц
Умножение матрицы А на матрицу В определено тогда и только тогда, когда число столбцов первой матрицы равно числу строк второй. В этом случае матрица А называется согласованной с матрицей В. Транспонированием матрицы называется замена строк матрицы на ее столбцы с сохранением их порядка. Обратной для матрицы А называется такая матрица (обозначение Если определитель матрицы отличен от нуля, то такая матрица называется невырожденной, если определитель матрицы равен нулю, то матрица называется вырожденной. Теорема: Обратная матрица Алгоритм вычисления обратной матрицы: 1. Находим определитель исходной матрицы. Если Если 2. Находим матрицу 3. Находим алгебраические дополнения элементов транспонированной матрицы и составляем из них присоединенную матрицу
4. Вычисляем обратную матрицу по формуле:
5. Проверяем правильность вычисления обратной матрицы
Любой квадратной матрице
и вычисляемое по определенным правилам: 1) Квадратная матрица первого порядка есть
2) Определитель квадратной матрицы второго порядка вычисляется по формуле:
3) Определитель квадратной матрицы третьего порядка вычисляется по формуле:
4) Определитель квадратной матрицы Иначе говоря, имеют место следующие равенства: · разложение определителя по элементам
· разложение определителя по элементам
Минором Алгебраическим дополнением
Примеры выполнения заданий. Пример 1. Вычислить: Решение: Ответ: Пример 2. Вычислить: Решение: Ответ: Пример 3. Найти Решение: Ответ: Пример 4. Вычислить: Решение:
Ответ: Пример 5. Даны матрицы А и В. Найдите: Решение: 1) 2) 3) 4) 5)
Ответ: Пример 6. Вычислите обратную матрицу: Решение: 1) Находим определитель:
2) Находим матрицу
3) Находим алгебраические дополнения элементов транспонированной матрицы:
Составляем из них присоединенную матрицу
4) Находим обратную матрицу:
Ответ: Задания для практической работы. Вариант 1
Практическая работа № 2. Краткое изложение темы. Примеры выполнения заданий. Пример 1. Найти решение системы уравнений методом Крамера: Решение:
1) Найдем главный определитель: D = 2) Найдем первый вспомогательный определитель Dх = 3) Найдем второй вспомогательный определитель Dу = 4) Найдем третий вспомогательный определитель Dz = 5) Найдем х, у и z по формулам Крамера x = Dх/D = 1; у = Dу/D = 2; z = Dz/D = 3. Ответ: x = 1, у = 2, z = 3. Пример 2. Найти х, у, z при помощи обратной матрицы: Решение: 1. Находим определитель системы: 2. Находим транспонированную матрицу 3. Находим присоединенную матрицу.
Следовательно: 4. Вычисляем обратную матрицу
5. Находим х, у, z.
Ответ: х=1, у=2, z=3. Задания для практической работы. Вариант 1.
Практическая работа № 3. Краткое изложение темы. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Метод Гаусса – это метод последовательного исключения переменных. Он заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного или трапецеидального вида, из которых последовательно, начиная с последних по номеру переменных, находятся все остальные. К элементарным преобразованиям относятся: 1. Прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на одно и то же число, не равное нулю. 2. Перестановка уравнений местами. 3. Удаление из системы уравнений, являющихся тождествами для всех Примеры выполнения заданий. Пример 1. Решите системы линейных уравнений методом Гаусса: Решение: Переставим третье уравнение на место первого:
Запишем расширенную матрицу
В следующей матрице первую строку оставим неизменной, а вторую и третью строки получим в результате умножения первой строки на 3, а затем на 2 и вычитанием поочередно первой и второй, а затем первой и третьей строк.
Разделим вторую строку на 8
Домножим вторую строку на 3 и из нее вычтем третью строку
Получили треугольную матрицу. Прямой ход выполнили. Обратный ход: последнюю строку матрицы запишем в виде уравнения. Получим:
Предпоследнюю строку матрицы запишем в виде
и подставим вместо z найденной значение 3
И далее, из первого уравнения получим
Итак, получили x = 1, y = 2, z = 3 Ответ: (1; 2;3)
Задания для практической работы. Вариант 1.
Практическая работа № 4. Краткое изложение темы. Комплексными числами называются числа вида 1) два комплексных числа 2) суммой двух комплексных чисел
3) произведением двух комплексных чисел Запись Любое действительное число Числа Числа Модулем комплексного числа называется число Аргументом комплексного числа называется угол Из определения тригонометрических функций следует, что если
Действия над комплексными числами сложение: вычитание: умножение: деление: Тригонометрическая форма комплексного числа
Действия над комплексными числами, заданными в тригонометрической форме: умножение:
деление:
возведение в
извлечение корня
где
Примеры выполнения заданий. Пример 1. Найти модуль и главное значение аргумента числа Решение: 1. Выполним деление: 2. Найдем модуль данного числа: 3. Найдем главное значение аргумента: Ответ:
Пример 2. Представить в тригонометрической форме число: Решение: Найдем модуль числа: Найдем главное значение аргумента:
Значит, или Ответ:
Пример 3. Возвести в степень Решение: Представим данное число в тригонометрической форме.
Итак, По формуле Муавра получим
Ответ:
Пример 4. Извлечь корни из комплексного числа Решение: Представим число 1 в тригонометрической форме: По формуле находим
если если если Ответ:
Пример 5. Решите уравнение Решение: Введем подстановку
Вычислим дискриминант Найдем корни уравнения Тогда
Ответ: Задания для практической работы. Вариант 1. 1. Найдите модуль и аргумент числа 2. Выполните действия: 3. Возведите в степень по формуле Муавра 4. Извлеките корень 5. Решите уравнение
Практическая работа № 5. Краткое изложение темы. Число А называется пределом функции
Свойства пределов: Если существуют 1) 2) 3) Используются также следующие пределы:
Правило Лопиталя раскрытия неопределенностей. Пусть в некоторой окрестности точки Примеры выполнения заданий. Пример 1. Найти предел Решение: Пример 2. Найти предел Решение: Имеем неопределенность вида
Пример 3. Найти предел Решение: Это – неопределенность вида Ответ: Пример 4. Найти предел Решение. Умножим числитель и знаменатель дроби на сопряженное число
Ответ: Пример 5. Найти предел Решение: Используя первый замечательный предел, имеем
Пример 6. Найти предел Решение. Ответ: Пример 7. Найти предел Решение: Делением числителя на знаменатель выделим целую часть:
Таким образом, при
Так как Учитывая, что Ответ: Пример 8. Найти Решение: Это – неопределенность вида
так как
Задания для практической работы. Вариант № 1. Вычислите пределы:
Практическая работа № 6. Краткое изложение темы. Примеры выполнения заданий. Задания для практической работы. Вариант № 1.
Практическая работа № 7. Краткое изложение темы. Частной производной от функции
Частной производной по у называется конечный предел
Для частных производных справедливы обычные правила и формулы дифференцирования. Примеры выполнения заданий. Пример 1. Найти частные производные ( Решение: Рассматривая у как постоянную величину, получим Рассматривая х как постоянную величину, получим Ответ: Пример 2. Найти частные производные ( Решение: Рассматривая у как постоянную величину, получим Рассматривая х как постоянную величину, получим Ответ: Пример 3. Найти частные производные (
Решение: Ответ: Задания для практической работы. Вариант 1. Найти частные производные следующих функций:
Практическая работа № 8. Краткое изложение темы. Определение: Множество всех первообразных функций f(x) в промежутке х называется неопределенным интегралом этой функции и обозначается так Свойства неопределенного интеграла: 1.
2. 3. 4. 5. Метод замены переменной. Пусть имеем
и x = φ(t) – непрерывно дифференцированная. Рассмотрим Итак, функция F(φ(t)) – есть первообразная для Следовательно:
Из (1) и (2) получаем следующее равенство.
На практике замену переменных производят, как правило, t = g(x). Определенный интеграл Определение. Приращение F(b) — F(a) любой из первообразных функций F(х) + С при изменении аргумента от х = а до х = b называется определенным интегралом и обозначается
Примеры выполнения заданий. Пример 1. Вычислить Решение: Согласно правилу имеем: Ответ: Пример 2. Вычислить Решение:
Ответ: Пример 3. Найти: Решение:
Ответ: Пример 4. Найти: Решение:
Ответ: Пример 5. Найти Решение: Вынесем множитель
Положим
тогда Находим новые пределы:
Следовательно
Ответ:
Задания для практической работы. Вариант 1. Найдите следующие интегралы:
Практическая работа № 9. Краткое изложение темы. Уравнение вида
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 109; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.126.5 (0.317 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
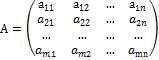 называется матрицей.
называется матрицей.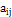 — действительные числа (i = 1, 2,..., m, j=1, 2,..., n), i и j — соответственно индексы строки и столбца.
— действительные числа (i = 1, 2,..., m, j=1, 2,..., n), i и j — соответственно индексы строки и столбца.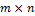 числа строк на число столбцов называют размером матрицы А.
числа строк на число столбцов называют размером матрицы А.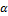 называется матрица, каждый элемент которой получен умножением соответствующего элемента матрицы А на число
называется матрица, каждый элемент которой получен умножением соответствующего элемента матрицы А на число  .
. называется такая матрица
называется такая матрица  , каждый элемент которой
, каждый элемент которой 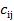 равен сумме произведений элементов
равен сумме произведений элементов 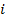 -ой строки матрицы А на соответствующие элементы
-ой строки матрицы А на соответствующие элементы  -го столбца матрицы В:
-го столбца матрицы В: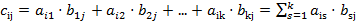 , где
, где  ,
, 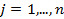 .
. ), которая удовлетворяет условиям
), которая удовлетворяет условиям 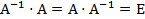 , где Е – единичная матрица.
, где Е – единичная матрица.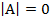 , то матрица А – вырожденная и обратной матрицы
, то матрица А – вырожденная и обратной матрицы 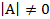 , то матрица А – невырожденная и обратная матрица
, то матрица А – невырожденная и обратная матрица  , транспонированную к матрице А.
, транспонированную к матрице А. .
.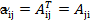 .
.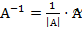 ,
, 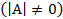 ;
; 
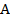 порядка
порядка 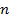 можно поставить в соответствие число, называемое определителем, обозначаемое следующим образом
можно поставить в соответствие число, называемое определителем, обозначаемое следующим образом
 , ее определитель:
, ее определитель: .
.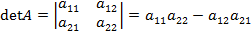 .
.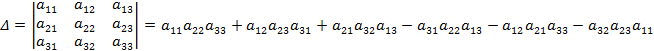 .
.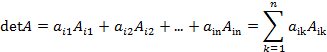
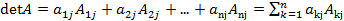 .
.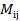 элемента
элемента 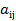 определителя
определителя  некоторого элемента
некоторого элемента  :
: .
.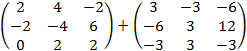 .
.
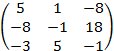



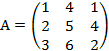 .
.

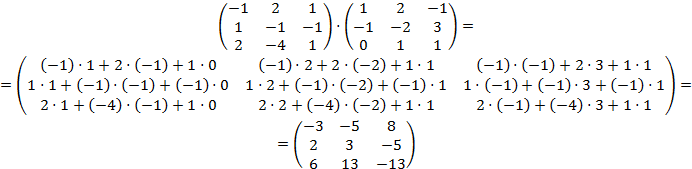

 ,
, 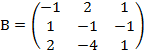
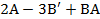 .
.

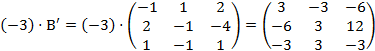

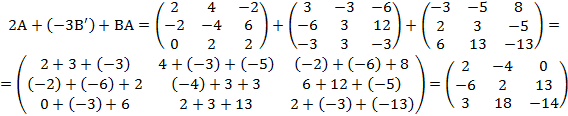
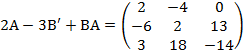 .
.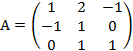 .
.
 , значит обратная матрица существует.
, значит обратная матрица существует.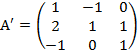 .
.
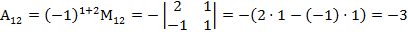


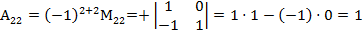


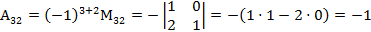
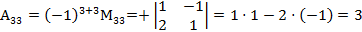

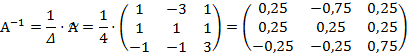
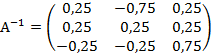

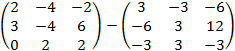
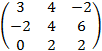

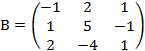 .
.
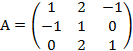

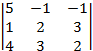 = 5∙2∙2 + 1∙3∙(-1) + (-1) ∙3∙4 - 4∙2∙(-1) - 1∙(-1) ∙2 – 3∙3∙5 = - 30;
= 5∙2∙2 + 1∙3∙(-1) + (-1) ∙3∙4 - 4∙2∙(-1) - 1∙(-1) ∙2 – 3∙3∙5 = - 30; = 0∙2∙2 + 14∙3∙(-1) + (-1) ∙3∙16 - 16∙2∙(-1) - 3∙3∙0 - 14∙(-1) ∙2= - 30.
= 0∙2∙2 + 14∙3∙(-1) + (-1) ∙3∙16 - 16∙2∙(-1) - 3∙3∙0 - 14∙(-1) ∙2= - 30.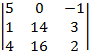 = 5∙14∙2 + 1∙16∙(-1) + 0∙3∙4 - 4∙14∙(-1) - 16∙3∙5 - 1∙0∙2 = - 60.
= 5∙14∙2 + 1∙16∙(-1) + 0∙3∙4 - 4∙14∙(-1) - 16∙3∙5 - 1∙0∙2 = - 60.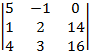 = 5∙2∙16 + 1∙3∙0 + (-1) ∙14∙4 - 4∙2∙0 - 3∙14∙5 - 1∙(-1) ∙16= -90.
= 5∙2∙16 + 1∙3∙0 + (-1) ∙14∙4 - 4∙2∙0 - 3∙14∙5 - 1∙(-1) ∙16= -90.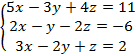
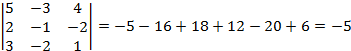 .
. .
.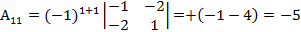 ,
,  ,
,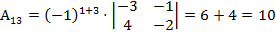 ,
,  ,
,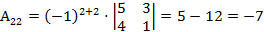 ,
, 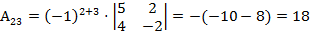 ,
, ,
, 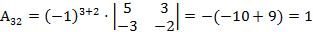 ,
,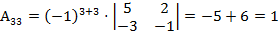 .
. .
.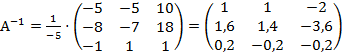 .
.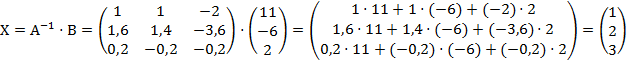
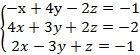


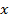 .
.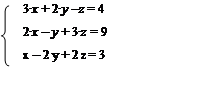
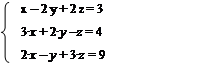

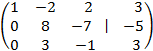

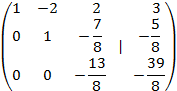
 ,
,
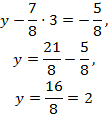

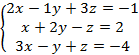


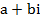 , где
, где 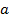 и
и 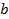 - действительные числа, а число
- действительные числа, а число 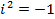 , называется мнимой единицей, если для этих чисел понятия равенства и действия сложения и умножения определены следующим образом:
, называется мнимой единицей, если для этих чисел понятия равенства и действия сложения и умножения определены следующим образом: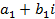 и
и 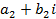 называются равными, если
называются равными, если 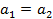 и
и 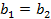 ,
,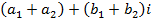 ,
,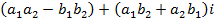 .
.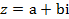 называется алгебраической формой записи комплексного числа, где
называется алгебраической формой записи комплексного числа, где 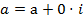 .
.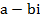 называются комплексно-сопряженными.
называются комплексно-сопряженными.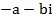 называются противоположными.
называются противоположными.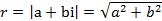 .
.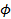 между действительной осью
между действительной осью 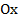 и вектором
и вектором 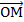 , отсчитываемый от положительного направления действительной оси. Записывается так:
, отсчитываемый от положительного направления действительной оси. Записывается так: 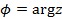 или
или 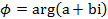 .
.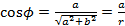 ,
, 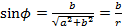 .
.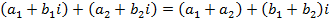 ,
,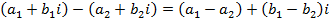 ,
,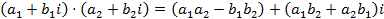 ,
,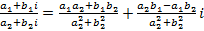 .
.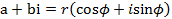 .
.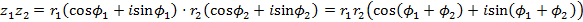 ,
,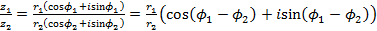 ,
,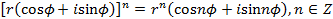 - формула Муавра,
- формула Муавра,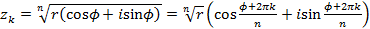 ,
,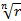 - арифметический корень,
- арифметический корень, 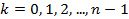 .
.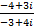 .
.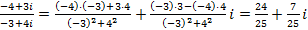
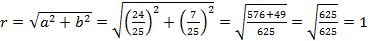 .
.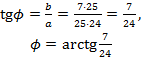
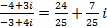 ,
, 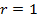 ,
, 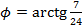 .
.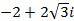 .
.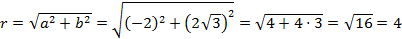 .
.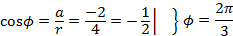
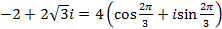
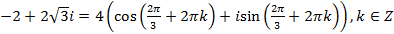
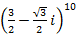 .
.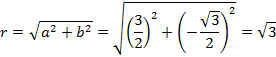
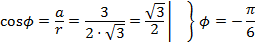
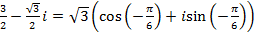 .
.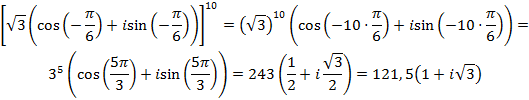
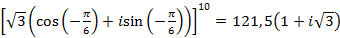
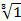 .
.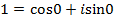 .
.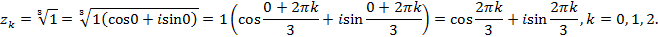
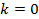 , то
, то 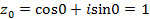 ,
,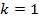 , то
, то 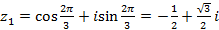 ,
,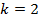 , то
, то 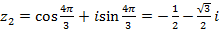 .
.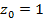 ,
, 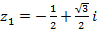 ,
, 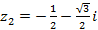 .
.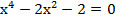 .
.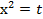 , тогда
, тогда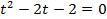
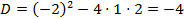 .
.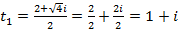 ,
, 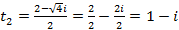 .
.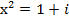 или
или
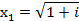
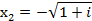
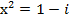
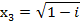
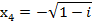
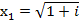 ,
, 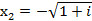 ,
, 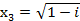 ,
, 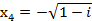 .
.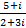 .
.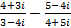 .
.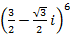 .
.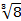 .
.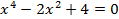 .
. при
при  , если для любого сколь угодно малого
, если для любого сколь угодно малого  найдется такое
найдется такое 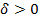 , что
, что 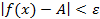 при
при  . Это записывают так:
. Это записывают так:  .
. и
и  , то
, то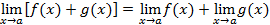 ,
,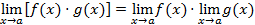 ,
,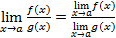 (при
(при 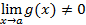 ).
). (первый замечательный предел);
(первый замечательный предел);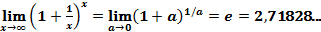 (второй замечательный предел).
(второй замечательный предел). (кроме, быть может, самой точки
(кроме, быть может, самой точки  и
и  дифференцируемы и
дифференцируемы и  . Если
. Если 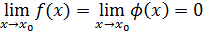 или
или  , т. е. частное
, т. е. частное  в точке
в точке 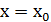 представляет собой неопределенность вида
представляет собой неопределенность вида  или
или  , то
, то  , если предел в правой части этого равенства существует.
, если предел в правой части этого равенства существует.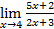 .
.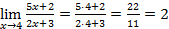 Ответ:
Ответ: 
 .
. . Разложим числитель и знаменатель на множители.
. Разложим числитель и знаменатель на множители. . Ответ:
. Ответ: 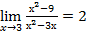
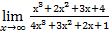 .
. . Разделим числитель и знаменатель дроби на старшую степень
. Разделим числитель и знаменатель дроби на старшую степень 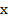 , т.е. на
, т.е. на  :
: 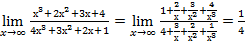 .
.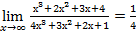 .
. .
.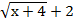
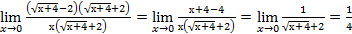 .
.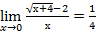 .
.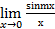 .
.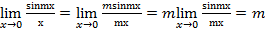 . Ответ:
. Ответ:  .
. .
.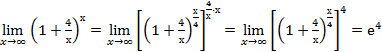 .
. .
.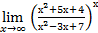 .
. .
.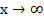 данная функция представляет собой степень, основание которой стремится к единице, а показатель – к бесконечности (неопределенность вида
данная функция представляет собой степень, основание которой стремится к единице, а показатель – к бесконечности (неопределенность вида  ). Преобразуя функцию так, чтобы использовать второй замечательный предел, получим
). Преобразуя функцию так, чтобы использовать второй замечательный предел, получим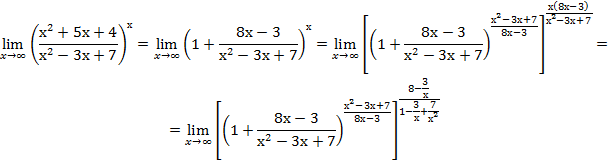
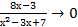 при
при 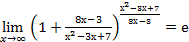 .
. , находим
, находим  .
. .
. ,
, . Здесь правило Лопиталя применено дважды. Ответ:
. Здесь правило Лопиталя применено дважды. Ответ:  .
.
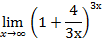
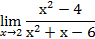

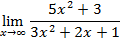
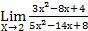 . Воспользуйтесь правилом Лопиталя.
. Воспользуйтесь правилом Лопиталя.

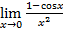 . Воспользуйтесь правилом Лопиталя.
. Воспользуйтесь правилом Лопиталя.

 . Воспользуйтесь правилом Лопиталя.
. Воспользуйтесь правилом Лопиталя.
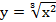 .
2.
.
2. 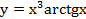 .
3.
.
3.  .
4.
.
4. 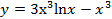 .
5.
.
5. 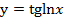 .
6.
.
6. 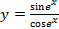 .
7.
.
7. 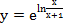 .
.
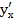 от неявных функций:
8.
от неявных функций:
8. 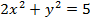 .
9.
.
9. 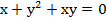 .
10.
.
10. 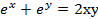 .
.
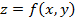 по независимой переменной х называется конечный предел
по независимой переменной х называется конечный предел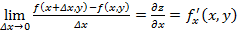 , вычисленный при постоянном у.
, вычисленный при постоянном у.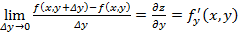 , вычисленный при постоянном х.
, вычисленный при постоянном х.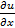 и
и 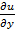 ).от функции:
).от функции: 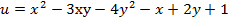
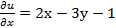 .
.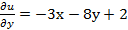 .
.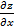 и
и 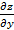 ) от функции:
) от функции: 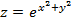 .
.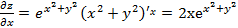 .
.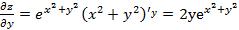 .
.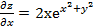 ,
, 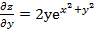 .
. и
и 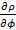 ) от функции:
) от функции: 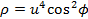 .
.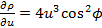 ,
, 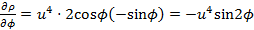 .
.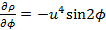 .
.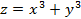
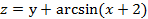
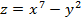
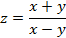
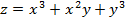
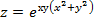 . Найти
. Найти 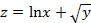
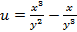 . Найти
. Найти 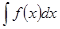 .
.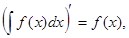 имеем
имеем
 (подынтегральному выражению).
(подынтегральному выражению). где k – постоянная.
где k – постоянная.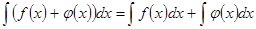

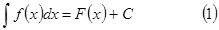
 - первообразная для f(x)∙φ′(t).
- первообразная для f(x)∙φ′(t).
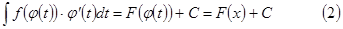
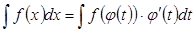 - формула замены переменной в неопределенном интеграле.
- формула замены переменной в неопределенном интеграле. .
.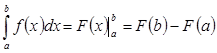 - формула Ньютона-Лейбница.
- формула Ньютона-Лейбница. .
.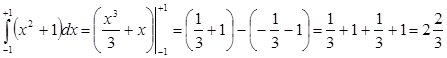 .
.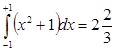
 .
.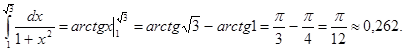
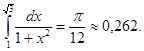
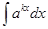
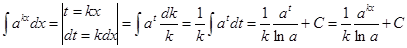




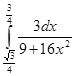 .
.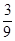 за знак интеграла:
за знак интеграла: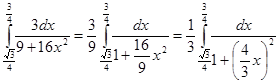 .
.
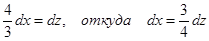 .
.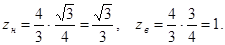
 .
.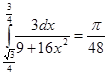 .
.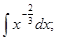
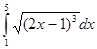
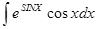
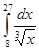
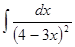

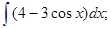


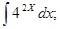
 ,
,


