
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: действия над комплексными числами.Содержание книги
Поиск на нашем сайте
Краткое изложение темы. Комплексными числами называются числа вида 1) два комплексных числа 2) суммой двух комплексных чисел 3) произведением двух комплексных чисел Запись Любое действительное число Числа Числа Модулем комплексного числа называется число Аргументом комплексного числа называется угол Из определения тригонометрических функций следует, что если
Действия над комплексными числами сложение: вычитание: умножение: деление: Тригонометрическая форма комплексного числа
Действия над комплексными числами, заданными в тригонометрической форме: умножение:
деление:
возведение в
извлечение корня
где
Показательная функция с комплексным показателем
В частности, при
Для комплексных показателей остаются в силе основные правила действий с показателями. Показательная функция имеет период, равный Показательная форма записи комплексного числа Действия над комплексными числами, заданными в показательной форме: умножение: деление: возведение в извлечение корня где
Примеры выполнения заданий. Пример 1. Найти модуль и главное значение аргумента числа Решение: 1. Выполним деление: 2. Найдем модуль данного числа: 3. Найдем главное значение аргумента:
Ответ:
Пример 2. Представить в тригонометрической форме число: Решение: Найдем модуль числа: Найдем главное значение аргумента:
Значит, или Ответ:
Пример 3. Возвести в степень Решение: Представим данное число в тригонометрической форме.
Итак, По формуле Муавра получим
Ответ:
Пример 4. Извлечь корни из комплексного числа Решение: Представим число 1 в тригонометрической форме: По формуле находим
если если если Ответ:
Пример 5. Решите уравнение Решение: Введем подстановку
Вычислим дискриминант Найдем корни уравнения Тогда
Ответ: Задания для практической работы. Вариант 1. 1. Найдите модуль и аргумент числа 2. Выполните действия: 3. Возведите в степень по формуле Муавра 4. Извлеките корень 5. Решите уравнение
Практическая работа № 5.
|
|||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 169; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.27.154 (0.006 с.) |

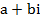 , где
, где 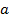 и
и 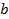 - действительные числа, а число
- действительные числа, а число 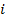 , определяемое равенством
, определяемое равенством 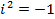 , называется мнимой единицей, если для этих чисел понятия равенства и действия сложения и умножения определены следующим образом:
, называется мнимой единицей, если для этих чисел понятия равенства и действия сложения и умножения определены следующим образом: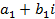 и
и 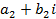 называются равными, если
называются равными, если 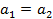 и
и 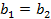 ,
,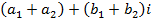 ,
,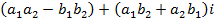 .
.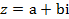 называется алгебраической формой записи комплексного числа, где
называется алгебраической формой записи комплексного числа, где 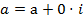 .
.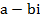 называются комплексно-сопряженными.
называются комплексно-сопряженными.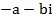 называются противоположными.
называются противоположными.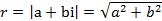 .
.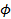 между действительной осью
между действительной осью 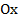 и вектором
и вектором 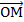 , отсчитываемый от положительного направления действительной оси. Записывается так:
, отсчитываемый от положительного направления действительной оси. Записывается так: 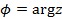 или
или 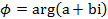 .
.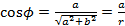 ,
, 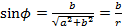 .
.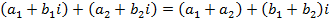 ,
,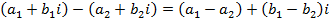 ,
,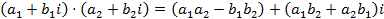 ,
,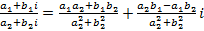 .
.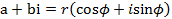 .
.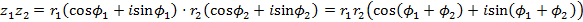 ,
,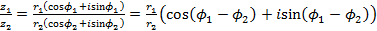 ,
,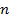 -ю степень:
-ю степень: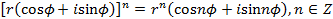 - формула Муавра,
- формула Муавра,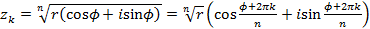 ,
,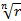 - арифметический корень,
- арифметический корень, 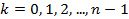 .
.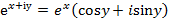 .
.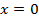 получается соотношение
получается соотношение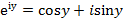 - формула Эйлера.
- формула Эйлера.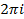 , т.е.
, т.е. 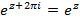 .
.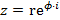 .
.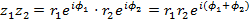 ,
,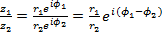 ,
,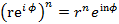 ,
,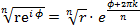 ,
,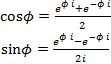 формулы Эйлера.
формулы Эйлера. .
.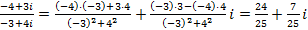
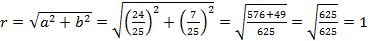 .
.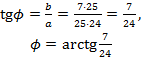
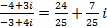 ,
, 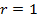 ,
, 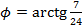 .
.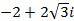 .
.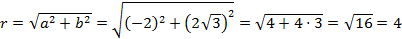 .
.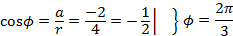
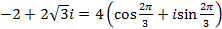
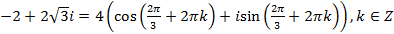
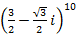 .
.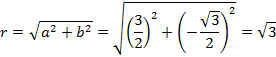
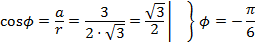
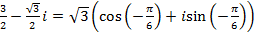 .
.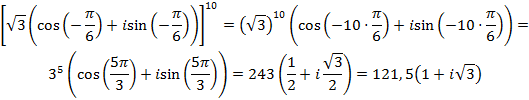
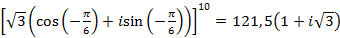
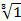 .
.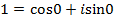 .
.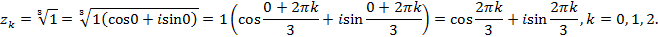
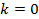 , то
, то 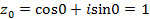 ,
,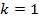 , то
, то 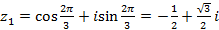 ,
,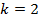 , то
, то 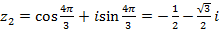 .
.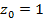 ,
, 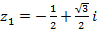 ,
, 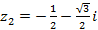 .
.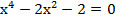 .
.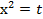 , тогда
, тогда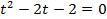
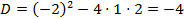 .
.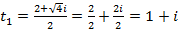 ,
, 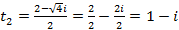 .
.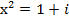 или
или
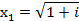
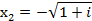
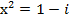
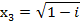
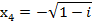
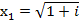 ,
, 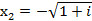 ,
, 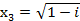 ,
, 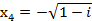 .
.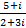 .
.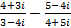 .
.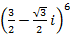 .
.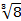 .
.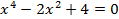 .
.


