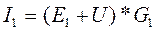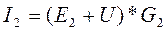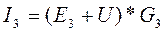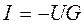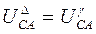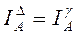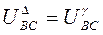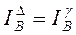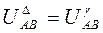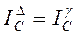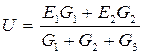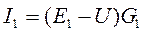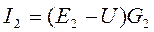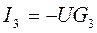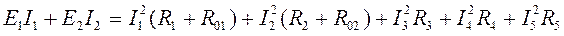Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
По выполнению практических занятий 1-11Содержание книги
Поиск на нашем сайте Методические указания По выполнению практических занятий 1-11 для специальности
13.02. 03 «Электрические станции, сети и системы»
2019
Методические указания Рассмотрены и утверждены На заседании цикловой комиссии энергетического профиля
Протокол № _____ от «____» ___________ 2019 г.
Председатель комиссии ___________И.Ю.Камардин
Методические указания составлены в соответствии с рабочей программой по дисциплине «Электротехника и электроника» по специальности 13.02.03.
_______________Л.В. Симон
Практическое занятие 1
Тема: «Расчёт батареи конденсаторов» Цель: Получить навыки расчёта батареи конденсаторов при различных соединениях: последовательном, параллельном, смешанном. Характер занятия: репродуктивный. Форма организации занятия: индивидуальная. Обеспечение занятия: методические указания, тетрадь для оформления практических занятий, письменные принадлежности, бланки заданий, конспект. Требования к знаниям и умениям студентов
Студент должен знать: -определение конденсатора и ёмкости; -способы соединения конденсаторов; -формулы для расчёта напряжения, заряда конденсатора, ёмкости; -единицы измерения ёмкости; уметь: -рассчитывать батарею конденсаторов при последовательном, параллельном и смешанном соединении, определять энергию батареи. Теория Конденсатор – это система, состоящая из двух проводников, изолированных друг от друга диэлектриком и обладающая свойством накапливать и удерживать на своих обкладках равные по величине, но противоположные по знаку электрические заряды. Каждый конденсатор обладает ёмкостью, которая характеризуется величиной заряда, который необходимо сообщить обкладкам конденсатора, чтобы изменить напряжение на 1 В.
Ёмкость рассчитывается по следующей формуле:
Способы соединения конденсаторов:
Последовательное соединение
U При последовательном соединении напряжение распределяется по отдельным конденсаторам и происходит уменьшение ёмкости.
U = U1 + U2 + U3, В
где U – общее напряжение, В U1,U2,U3 – напряжение на отдельных конденсаторах, В
Q – сonst (неизменная величина), т.е. величина заряда постоянна на каждом конденсаторе.
где С – общая ёмкость, Ф С1, С2, С3 – ёмкость на каждом конденсаторе, Ф
Параллельное соединение
C 2
C 3
U
При параллельном соединении U – const, неизменно на каждом конденсаторе
Q = Q1 + Q2 + Q3, Кл
где Q – общий заряд, Кл Q1,Q2,Q3 – заряд на отдельных конденсаторах, Кл
С = С1 + С2 + С3, Ф
где С – общая ёмкость, Ф С1, С2, С3 – ёмкость на каждом конденсаторе, Ф
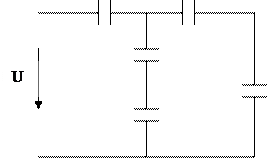
Смешанное соединение
C 4 C 3
C 5
Энергия батареи рассчитывается по формуле:
где С – ёмкость батареи конденсаторов, Ф U – напряжение, В
Порядок выполнения работы
1. Записать тему, цель, исходные данные своего варианта. 2. Принять, что все конденсаторы соединены последовательно, зарисовать схему. 3. Рассчитать батарею конденсаторов при последовательном соединении. Определить: а) общую ёмкость по формуле:
б) заряд на каждом конденсаторе по формуле Q = Собщ.Uобщ., который равен общему заряду; в) напряжение на каждом конденсаторе по формуле г) энергию батареи конденсаторов по формуле 4. Принять, что все конденсаторы соединены параллельно, зарисовать схему. 5. Рассчитать батарею конденсаторов при параллельном соединении. Определить: а) Общую ёмкость по формуле: Собщ = С1+С2+С3+С4+С5
б) Общий заряд конденсаторов по формуле: Q=Cобщ·Uобщ г) Напряжение на каждом конденсаторе равно общему напряжению д) Энергию батареи конденсаторов по формуле:
6. Начертить схему смешанного соединения, соответствующую своему заданию. 7. Рассчитать батарею конденсаторов при смешанном соединении.
Определить напряжение и заряд каждого конденсатора, энергию батареи.
8. Сдать работу преподавателю.
Система оценки: пятибальная.
Задача
Даны 5 конденсаторов и их ёмкость С1, С2, С3, С4, С5, дано подаваемое напряжение. Определить напряжение и заряд каждого конденсатора, энергию батареи конденсаторов при последовательном, параллельном и смешанном соединении (соответственно рисунок для данного варианта).
Таблица 1
C1
C2 С3
 
                    
                      
                   
                   
Контрольные вопросы 1. Что называется конденсатором? 2. Чему равна ёмкость при последовательном соединении? 3. Чему равна ёмкость при параллельном соединении? 4. Что можно сказать о напряжении при различных способах соединения? 5. Чему равна энергия конденсатора? 6. Как измерить ёмкость конденсаторов? 7. В каких единицах измеряется ёмкость, соотношение между единицами?
Список использованной литературы 1 Евдокимов Ф.Е. «Теоретические основы электротехники», Москва «Высшая школа», 1999.
Практическое занятие 2
Теория
Электрическая цепь – это совокупность устройств и объектов, образующих путь электрического тока. Классификация электрических цепей: - по виду тока: цепи постоянного и переменного тока; - по составу элементов: цепи активные и пассивные, цепи линейные и нелинейные; - по характеру распределения параметров: цепи с сосредоточенными и распределенными параметрами; - по числу фаз (для цепей переменного тока): однофазные, многофазные.
Элемент электрической цепи – отдельное устройство, входящее в состав электрической цепи и выполняющее в ней определенную функцию.
Закон Ома
Ток на данном участке цепи прямопропорционален напряжению на этом участке и обратнопропорционален его сопротивлению.
Порядок выполнения работы 1. Записать тему, цель, исходные данные своего варианта. 2. Найти общее сопротивление цепи путем последовательного преобразования схемы. 3. Найти ток внеразветвленной части цепи по формуле: 4. Найти ток и напряжение на каждом участке цепи, разворачивая схему. 5. Проверить правильность решения, составив баланс мощностей:
6. Сделать вывод о правильности решенной задачи. 7. Сдать работу преподавателю.
Система оценки – пятибальная
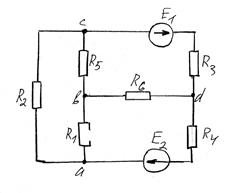
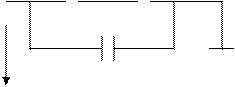
задание на расчет
Схема № 3
Схема № 5
Метод упрощения или сворачивания схемы заключается в следующем: Рассмотрим на примере
1. R3 и R4 соединены последовательно Þ R34=R3+R4 Схема будет выглядеть следующим образом
2. R2 и R34 соединены параллельно Þ Схема будет выглядеть следующим образом
3. R1, R5, R234 соединены последовательно Þ эквивалентное сопротивление будет равно 4. Необходимо найти ток внеразветвленной части цепи по формуле: 5. Теперь необходимо определить ток и напряжение на каждом участке постепенно сворачивая схему
6.
7.
Таким образом, были найдены токи и напряжения на каждом участке.
контрольные вопросы 1. Что такое электрическая цепь, элемент электрической цепи? 2. Закон Ома. Сформулировать и записать. 3. Способы соединения потребителей. 4. Что можно сказать о напряжении и токе при различных способах соединения? 5. Чему равно общее сопротивление цепи при последовательном и параллельном соединении?
список использованной литературы
1 Евдокимов Ф.Е. «Теоретические основы электротехники», Москва «Высшая школа», 1999г. Практическое занятие 3
Теория
Узловым напряжением называется разность потенциалов между данным узлом и базисным. Порядок расчета задач методом узлового напряжения: 1. Указать направление тока в ветвях. 2. Определить проводимость каждой ветви. 3. Определить узловое напряжение. 4. Найти токи в каждой ветви. Проводимость ветви равна:
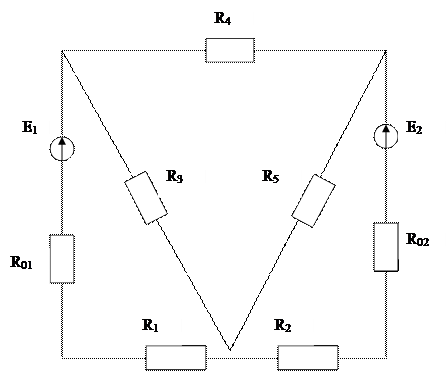
где R – сопротивление ветви, Ом Пример схемы, состоящей из двух узлов:
Для данной схемы узловое напряжение можно найти по формуле:
где E1, E2, E3 – ЭДС каждой ветви, B G1, G2, G3, G – проводимость каждой ветви, См Токи в каждой ветви данной схемы находятся по формулам:
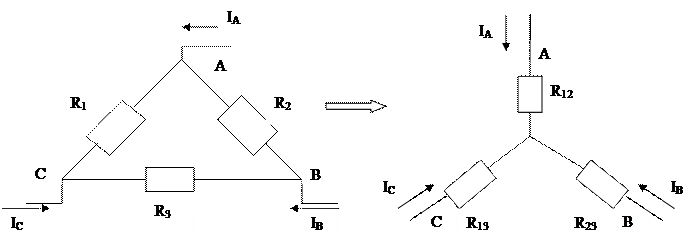
На примере можно рассмотреть: - преобразование треугольника сопротивления в эквивалентную звезду
Условия преобразования
Порядок выполнения работы 1. Записать тему, цель, исходные данные своего варианта. 2. В данной схеме преобразовать треугольник сопротивлений в эквивалентную звезду и рассчитать сопротивления лучей звезды. 3. Указать направление тока в каждой ветви, полученной схемы. 4. Определить проводимость каждой ветви.
5. Определить узловое напряжение по формуле:
6. Найти токи в каждой ветви по формулам:
7. Перейти от преобразованной схемы к первоначальной и определить токи на каждом участке. Для этого следует воспользоваться первым и вторым законами Кирхгофа для первоначальной схемы.
8. Проверить правильность решения, составив баланс мощностей:
9. Сделать вывод о правильности решенной задачи. 10. Сдать работу преподавателю.
Система оценки – пятибальная
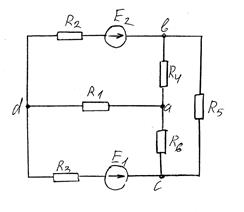
Задание на расчет
Контрольные вопросы
1. Что называется узловым напряжением? 2. Записать формулу расчета узлового напряжения. 3. Что такое проводимость? 4. Записать формулы преобразования треугольника сопротивлений в эквивалентную звезду. 5. Назвать порядок расчета задачи методом узлового напряжения.
список использованной литературы
1 Евдокимов Ф.Е. «Теоретические основы электротехники», Москва. «Высшая школа», 1999г. Практическое занятие 4
Теория
Первый закон Кирхгофа Сумма токов узла равна нулю: SI=0 Второй закон Кирхгофа Во всяком замкнутом контуре алгебраическая сумма ЕДС равняется алгебраической сумме падений напряжений на участках контура: SE=SIR Контурный ток – это некоторая расчетная величина, которая одинакова для всех ветвей данного контура. Порядок расчета задач методом контурных токов: 1. Условно задается направление тока. 2. Определяется число уравнений (число уравнений равно числу неизвестных). 3. Составляем уравнения (по первому закону составляем число уравнений на единицу меньше числа узлов). 4. Решаем уравнения. 5. Делаем вывод.
Потенциальная диаграмма – это график распределения потенциала вдоль замкнутого контура электрической цепи. Для построения диаграммы необходимо определить направление тока в цепи и найти его значение. Затем разбить цепь на отдельные участки и определить потенциал каждого участка. Строить потенциальную диаграмму необходимо в прямоугольной системе координат по вертикальной оси отложить значение потенциала, по горизонтальной – сопротивление каждого участка, причем прибавляя к одному сопротивлению сопротивление следующего участка. Таким образом, по горизонтальной оси будет отложено в масштабе все сопротивление цепи. Порядок выполнения работы 1. Записать тему, цель, исходные данные своего варианта. 2. Задать направление тока в каждом контуре. 3. Составить систему уравнений, используя 2-ой закон Кирхгофа. 4. Решить данную систему уравнений и находим контурные токи (II, III, IIII). 5. Найти токи на каждом участке цепи (I1, I2, I3…). 6. Проверить правильность решения, составив баланс мощностей. 7. Начертить потенциальную диаграмму для внешнего контура цепи. 8. Сделать вывод. 9. Сдать работу преподавателю
Система оценки – пятибальная
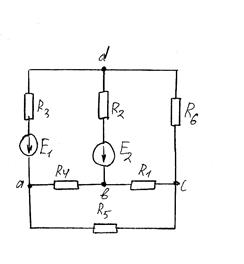
Задание на расчет
Схема № 1 Схема № 2
Схема № 3 Схема № 4
Схема № 5 Схема № 6
Познавательные статьи:
|
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 190; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

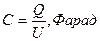
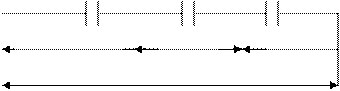 С1 С2 С3
С1 С2 С3
 U1 U2 U3
U1 U2 U3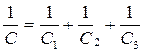
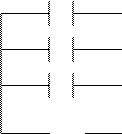 C 1
C 1 
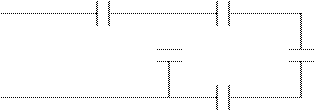 C 1 C 2
C 1 C 2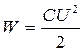 , Дж
, Дж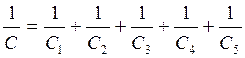 ;
;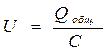 ;
;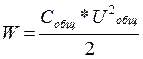
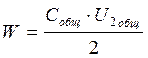








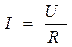
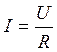
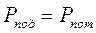 (подаваемая мощность должна быть равна потребляемой)
(подаваемая мощность должна быть равна потребляемой)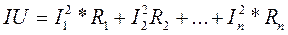
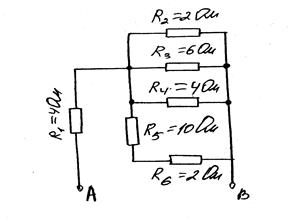 Схема № 1 Схема № 2
Схема № 1 Схема № 2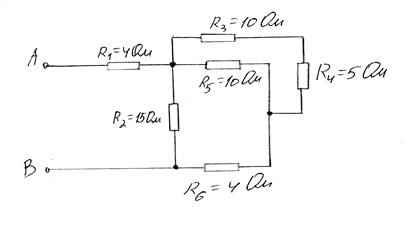
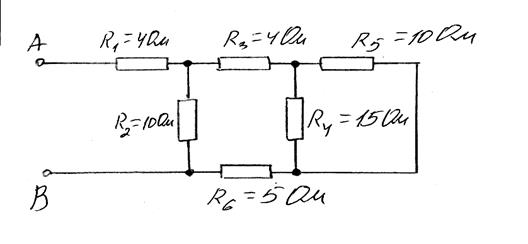
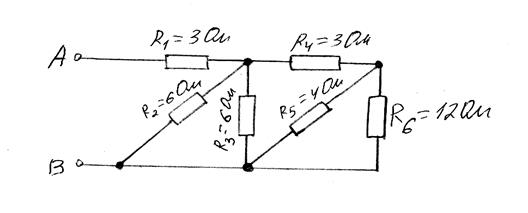
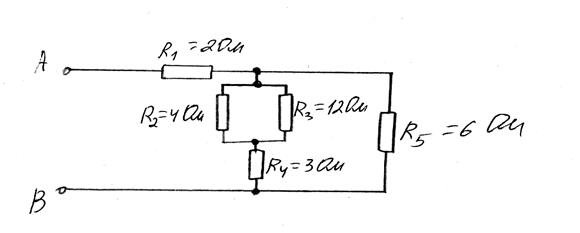
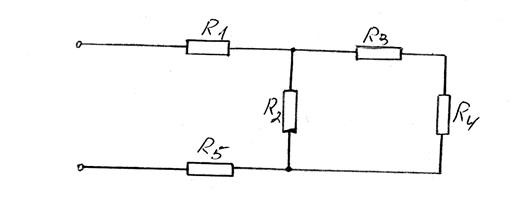
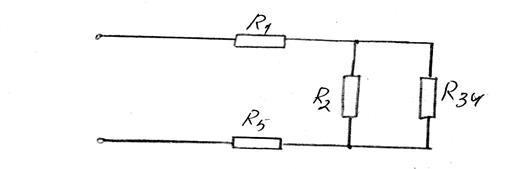

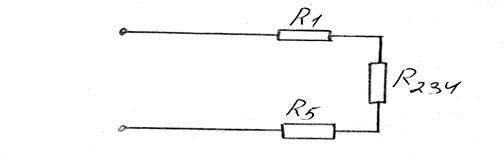
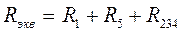
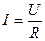 .
.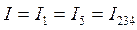 , т.к. соединение последовательное, а напряжения будет равны:
, т.к. соединение последовательное, а напряжения будет равны: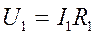
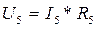
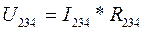
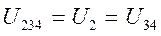 , т.к. соединение параллельное, токи будут равны:
, т.к. соединение параллельное, токи будут равны: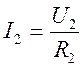
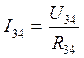
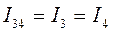 , т.к. соединение последовательное, а напряжения равны:
, т.к. соединение последовательное, а напряжения равны: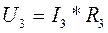
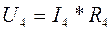
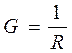 , См (сименс)
, См (сименс)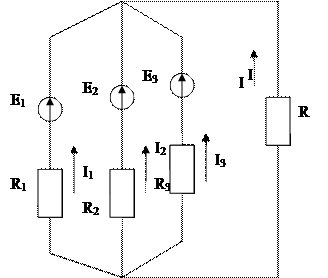
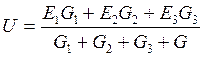 ; B
; B