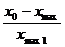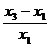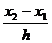Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Крутопадающий пласт, бесконечныйСодержание книги Поиск на нашем сайте
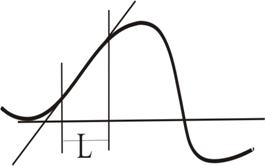
По простиранию и падению
h = L / К2 (8.12) l = Zmax / К ´ 2 = Z ´ max h / K 11 2
В этих формулах коэффициенты зависят от относительной горизонтальной мощности пласта (2 b / h), определяемой по отношению L / Хмах (Хма х – абсцисса точки пересечения касательной к точке перегиба с касательной к точке максимума кривой). Значения нужных величин для определения глубины залегания намагниченных тел приведены в табл. 8.3.
Таблица 8.3
Для аномалий D Z при косой намагниченности и аномалии D Т методика определения h и l остается той же. Если кривые асимметричны, то пользуются средними значениями L и хма х по правой и левой ветвям кривой. Исключение из этого правила представляют аномалии D Z и D Т при косой намагниченности, когда направление вектора намагниченности менее 30о-40о. Аномальные кривые становятся настолько асимметричными, что определения по обеим ветвям становятся затруднительными и для нахождения h нужно применять формулу для вертикального контакта. По кривым D Т при косой намагниченности и при большой мощности (2 b ³10 h), при простирании аномалий под углом к магнитному меридиану (резко асимметричные аномалии) глубины получаются завышенными до 50% и более.
Пласты, ограниченные по простиранию и падению Для определения h и l тел, имеющих ограниченные размеры по простиранию и вертикали, существуют формулы:
где хо и х ma x – абсциссы точек пересечения касательной к точке перегиба с касательными к точкам максимума и минимума кривой, х1/4 и х0.1 – абсциссы точек, где Z или Т равно ¼ Zma x и 0.1 Zma x (cчитая от минимума Z). Значения коэффициентов К зависят от отношения b / h, определяемого по величине отношения Коэффициенты К для вертикального пласта при l =4 h представлены в табл. 8.4. Таблица 8.4
Изометричные и цилиндрические тела Глубина залегания центра изометричных и цилиндрических тел может оценивается с учетом специальных коэффициентов, вычисленных по величине расстояний между точками пересечения касательных. В таблице 8.5 представлены коэффициенты К для цилиндра и шара, приведены для их вычисления формулы, использующие следующие точки на аномальных кривых: х3 – точка пересечения касательных, проведенных к точке перегиба и минимуму аномальной кривой, х1 – точка пересечения касательных, проведенных к точке перегиба и максимуму, х2 – расстояние от абсциссы Zmax до абсциссы точки перегиба. Таблица 8.5
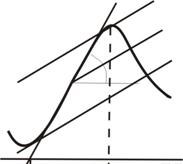
Метод Л.Петерса В зарубежной практике при экспресс-интерпретации магнитных аномалий широко используют метод касательных в варианте Л.Петерса. По его методу проводят касательную в точке перегиба аномальной кривой и биссектрису угла b, составляемого этой касательной и осью абсцисс, а затем – две касательные к аномальной кривой, параллельные биссектрисе (рис.8.7).
∆Х
Рис.8.7. Вариант Л.Д. Петереса Разность абсцисс D Х (8.14)точек пересечения касательных к аномальной кривой связана с глубиной залегания возмущающего объекта соотношением справедливым для широкого набора пластообразных тел
D Х = 1.6 h. (8.14)
Метод S. Breiner За рубежом для экспресс-интерпретации магнитных аномальных графиков широко используется метод касательных с прослеживанием размеров площадки касания в точке перегиба. S.Breiner установил, что глубина залегания h магнитного источника зависит от длины L прослеживаемости участка совмещения касательной, проведенной в точке перегиба, с аномальным графиком (рис. 8.8). Глубину залегания магнитных источников определяют по формуле
h = К L. (8.15)
Коэффициент пропорциональности К зависит от формы возмущающего объекта и изменяется в пределах от 0.5 до 1.5.
Рис.8.8. Метод S.Breiner
Несколько иные модификации метода касательных предложены другими авторами. В частности, обращено внимание на необходимость учета формы тела. В случае интерпретации аномалий над моделями неограниченного распространения на глубину следует в формуле (8.7) выражение в квадратной скобке умножить на коэффициент К. Значения коэффициента для тел различной формы и порядок учета обстоятельно исследованы В. К. Пятницким /21/. Метод касательных сразу после его предложения стал широко применяться при обработке магнитограмм аэромагнитной съемки. Оператор, определяя зарегистрированные максимумы, получал результаты в большом количестве точек. Очевидно, для слаболокализованных максимумов глубины получались большими, и на карту наносились только точки с минимальными глубинами. Построенная по значениям этих глубин карта поверхности, как это было установлено, соответствовала поверхности кристаллического фундамента. Благодаря этому метод касательных при изучении платформенных территорий приобрел важное значение; совершенствованию метода посвящена монографическая литература.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 132; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.24.226 (0.009 с.) |

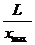
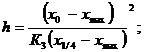
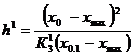 , (8.13)
, (8.13)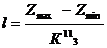 ,
,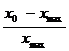 для пласта при l = 4 h.
для пласта при l = 4 h.