Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы истолкования магнитных аномалийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Однородно намагниченный шар Совмещая начало координат с эпицентром вертикально намагниченного шара при глубине его центра h, возьмем на профиле так называемые характерные точки с абсциссами х1/2 (аномалия в два раза меньше, чем в начале координат), х0 (при Z = 0) и x min (при отрицательном Zmin). Если на основании формул (7.2 и 7.3) написать для аномалий явные выражения (включая и начало координат), то для определения глубины h можем получить формулы
h = 2 x 1/2,
h =
h = 0,5 х min.
Данные формулы получены на основе исследования кривой Z (x). При х=0 аномалия Z достигает максимального значения:
Zmax = 2 M / h 3.
Так как Zmin составляет около 2% от Zmax (0), т.е. Zmax больше Zmin приблизительно в 50 раз, поэтому амплитуда Zmin определяется неуверенно, и последняя формула не может быть достоверной. Исследуя график горизонтальной составляющей Н (х), нетрудно установить, что расстояние х э от эпицентра аномалии до Нмах равно
x э = ± 0.5 h. Подставляя полученное значение в уравнение Н (2.3), находим
Нэ = 0.43 Zmax.
Определив h, из любого Z (7.2) или Н (7.3) находим М. Магнитный момент шара М = J υ, где J в общем случае представляет собой сумму остаточной и индуцированной намагниченности. Заимствуя значение намагниченности в априорных сведениях, вычисляем объем υ шара, а по нему – радиус шара.
8.2.2. Круговой двухмерный цилиндр
Для вертикально намагниченного двухмерного кругового цилиндра из формул (7.11) получаем аналогично
h = 2 x 1/2, (8.2) h = х0.
В случае аномальных графиков, отображающих наличие у тел косой намагниченности, следует к ним применить разложение, рассмотренное в параграфе 7.1, на две функции. Используя симметричный график, далее можно провести вычисления по вышеприведенным формулам. В геологической практике магниторазведки редко приходится встречаться с телами в форме круговых цилиндров. Однако современные условия производства потребовали решения новых экологических задач инженерной геофизики. Возникла необходимость контроля за состоянием трубного хозяйства страны, применение модели цилиндра оказалось актуальным и поставило ее на одно из приоритетных мест при моделировании в исследованиях данной проблемы. При решении обратных задач весьма эффективным является применение теоретических графиков, приводимых в атласах. Для сопоставления необходимо наблюденный график перестроить, т.е. дать его в масштабе теоретического. Совпадение графиков означает, что задача интерпретации решена. В атласах приведены графики для вертикально и косо намагниченных шара, цилиндров, а также других тел: эллипсоидов, эллиптических цилиндров, синклиналей, тел с прямоугольным сечением и т. д. Использование этих графиков позволяет существенно упростить операцию интерпретации. Подобранное по атласу намагниченное тело представляет результат решения обратной задачи в первом приближении. Для уточнения решения нужно контур теоретического тела подправить, чтобы уменьшить расхождение эффектов. Полученное таким способом решение обратной задачи называется методом подбора. Эта операция эффективнее выполняется при помощи ЭВМ, необходимо учитывать, что положение основного тела достовернее определяется путем расчета выпуклого тела.
Вертикальный тонкий пласт неограниченного Распространения по глубине Вид аномального графика над намагниченным телом пластообразной формы зависит от соотношения горизонтальной мощности верхней кромки пласта (2в) и глубины (h) его залегания. Обычно тонкими пластами считают тела, у которых 2в / h £ 1. Анализ аномальных кривых Z и Н над тонким пластом неограниченного распространения на глубину (рис. 7.8) и их функционалов (7.15) показывает: при х=0, над эпицентром пласта, горизонтальная составляющая Н = 0, а вертикальная составляющая Z принимает максимальное значение:
Z мах = 2М / h, Нмах = 0.5 Zмах,
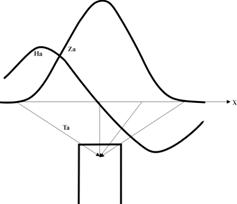
при х1 = ± h значения Н имеют абсолютную величину 0.5 Zmax, отрицательных значений Z не имеет, вектор Т во всех точках наблюдения направлен в верхний край пласта, с удалением от эпицентра аномалии графики Z и Н убывают медленно, стремясь к нулевым значениям только на бесконечных расстояниях. Значения глубины до верхней кромки тонкого пласта можно получить с помощью графиков по точке пересечения векторов Та (рис. 8.3) или по формулам . h = x
h = xi . (8.3)
h = x i
При интерпретации таких аномалий определяют глубину верхнего края пласта h.
Рис. 8.3. К интерпретации магнитных аномалий над тонким пластом
Горизонтальная пластина
Как следует из формул (7.21),кривая Z имеет пять точек экстремальных значений. По оценке Z (х=0) =
(8.7)
Точки х1,2 соответствуют Zmin, а точки х3, 4 имеют реальное значение при условии b > h
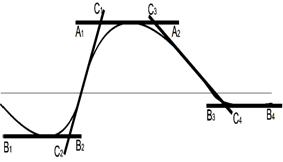
Если имеется кривая Н, то по аналогии можно найти связимежду ее характерными точками и элементами залегания пласта. 8. 3. Метод касательных Методы касательных основаны на аналитической зависимости ряда характерных точек кривой от параметров возмущающих объектов. В качестве основной исходной точки выбирают точку перегиба кривой исходного поля. Поэтому зависимость между координатами этой точки и параметрами возмущающих объектов выражается не через исходное поле, а через его производную в этой точке. В качестве дополнительных точек для составления системы уравнений выбираются любые другие точки: максимального и минимального значения поля, половины максимального значения; точки, где касательные к графику имеют наклон в два раза меньше, чем наклон основной касательной. Формулы для расчета глубин намагниченных объектов получаются из системы уравнений касательных, проведенных к точке перегиба и к какой-либо другой точке. Для каждой конкретной модели эти формулы будут иметь свои зависимости и могут быть использованы только для этого класса моделей. Способ касательных является эвристическим, т.е. получен без учета теории магниторазведки. Геофизик Ю.H. Грачев на примере аномальных графиков над шаром и круговым цилиндром по расстояниям между точками пересечения касательных, проведенных к характерным точкам заданной функции, нашел возможность определять глубину до поверхности (не до центра) магнитного источника. На рис.8.5 A 1 A 2 ‑ касательная в точке максимума, В1В2 и В3В4 – касательные в точках минимумов и C 1 C 2 и C 3 C 4 ‑ касательные в точках перегиба. Обозначая х1, х2, х3 и х4 ‑ абсциссы точек пересечения касательных, по разностям х2–х1 и х4–х3 предлагается находить глубину по следующей формуле:
h =
Рис.8.5. К определению глубины залегания магнитного тела способом касательных
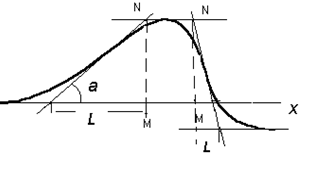
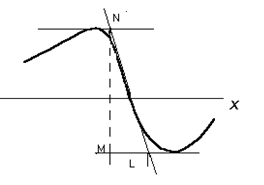
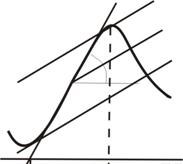
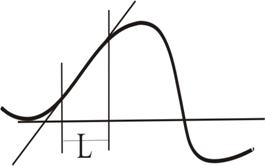
За рубежом этот метод называют методом наклона, так как он использует величину горизонтального градиента или наклон графика аномалии в точке перегиба. Метод основан на эмпирических наблюдениях, по данным которых установлен множитель К, являющийся коэффициентом пропорциональности между искомой глубиной и горизонтальным отрезком по оси Х = L, отсекаемым касательными. По графику аномальной кривой проводят касательные в точке положительного и отрицательного экстремума и в точке максимального градиента, т.е. в точке перегиба кривой (рис. 8.6). Полученная длина отрезка L в масштабе графика является функцией глубины и формы тела.
Рис.8.6. Модификации метода касательных
По изменению графика представим
L = MN / tg
где MN – наибольшая амплитуда, а Таблица 8.1
Значения глубины тела h в долях отрезка L, т. е. величины h: L для различных форм тел, приводятся в табл. 8.1. Рассмотрим практические методы определения глубины залегания некоторых тел.
8.3.1.Вертикальный контакт Глубину залегания верхней кромки h и намагниченности J определяют по формулам
h = L / К1,
и J = Z ´ max h / К 1 ´, (8.10) где L =
и Z ´ max =
Значения коэффициентов К1 и К2 зависят от относительной вертикальной мощности (l) пород контакта – сброса (l / h), определяемой по отношению 2 хэ: L, где х э – абсцисса максимума и минимума кривой. Значения величин, необходимых для определения h и J, приведены в табл.8.2.
Таблица 8.2
Определив h и l, находим глубину залегания нижней кромки тела: H = h + l. (8.11)
По простиранию и падению
h = L / К2 (8.12) l = Zmax / К ´ 2 = Z ´ max h / K 11 2
В этих формулах коэффициенты зависят от относительной горизонтальной мощности пласта (2 b / h), определяемой по отношению L / Хмах (Хма х – абсцисса точки пересечения касательной к точке перегиба с касательной к точке максимума кривой). Значения нужных величин для определения глубины залегания намагниченных тел приведены в табл. 8.3.
Таблица 8.3
Для аномалий D Z при косой намагниченности и аномалии D Т методика определения h и l остается той же. Если кривые асимметричны, то пользуются средними значениями L и хма х по правой и левой ветвям кривой. Исключение из этого правила представляют аномалии D Z и D Т при косой намагниченности, когда направление вектора намагниченности менее 30о-40о. Аномальные кривые становятся настолько асимметричными, что определения по обеим ветвям становятся затруднительными и для нахождения h нужно применять формулу для вертикального контакта. По кривым D Т при косой намагниченности и при большой мощности (2 b ³10 h), при простирании аномалий под углом к магнитному меридиану (резко асимметричные аномалии) глубины получаются завышенными до 50% и более.
Метод Л.Петерса В зарубежной практике при экспресс-интерпретации магнитных аномалий широко используют метод касательных в варианте Л.Петерса. По его методу проводят касательную в точке перегиба аномальной кривой и биссектрису угла b, составляемого этой касательной и осью абсцисс, а затем – две касательные к аномальной кривой, параллельные биссектрисе (рис.8.7).
∆Х
Рис.8.7. Вариант Л.Д. Петереса Разность абсцисс D Х (8.14)точек пересечения касательных к аномальной кривой связана с глубиной залегания возмущающего объекта соотношением справедливым для широкого набора пластообразных тел
D Х = 1.6 h. (8.14)
Метод S. Breiner За рубежом для экспресс-интерпретации магнитных аномальных графиков широко используется метод касательных с прослеживанием размеров площадки касания в точке перегиба. S.Breiner установил, что глубина залегания h магнитного источника зависит от длины L прослеживаемости участка совмещения касательной, проведенной в точке перегиба, с аномальным графиком (рис. 8.8). Глубину залегания магнитных источников определяют по формуле h = К L. (8.15)
Коэффициент пропорциональности К зависит от формы возмущающего объекта и изменяется в пределах от 0.5 до 1.5.
Рис.8.8. Метод S.Breiner
Несколько иные модификации метода касательных предложены другими авторами. В частности, обращено внимание на необходимость учета формы тела. В случае интерпретации аномалий над моделями неограниченного распространения на глубину следует в формуле (8.7) выражение в квадратной скобке умножить на коэффициент К. Значения коэффициента для тел различной формы и порядок учета обстоятельно исследованы В. К. Пятницким /21/. Метод касательных сразу после его предложения стал широко применяться при обработке магнитограмм аэромагнитной съемки. Оператор, определяя зарегистрированные максимумы, получал результаты в большом количестве точек. Очевидно, для слаболокализованных максимумов глубины получались большими, и на карту наносились только точки с минимальными глубинами. Построенная по значениям этих глубин карта поверхности, как это было установлено, соответствовала поверхности кристаллического фундамента. Благодаря этому метод касательных при изучении платформенных территорий приобрел важное значение; совершенствованию метода посвящена монографическая литература.
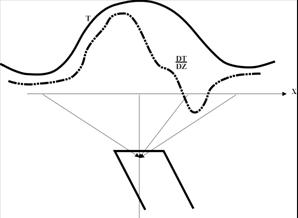
Векторные диаграммы Наблюденные или вычисленные градиенты Т можно использовать для экспрессной оценки глубины залегания намагниченных источников.
Рис.8.10. Построение векторных диаграмм
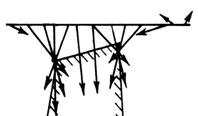
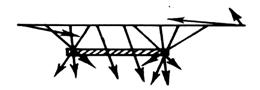
Для этого удобнее их представлять в векторной форме; градиент Векторное аномальное магнитное поле дает информацию об локальных особенностях геологического разреза, а места пересечения градиентных векторов показывают на наличие особых точек магнитных источников и их глубине залегания. Метод построения векторных диаграмм (рис.8.10) может быть достаточно эффективен при интерпретации магнитных аномалий над простыми геологическими структурами. На рис. 8.11 представлены векторные диаграммы для штокообразной модели (а), мощного пласта (в) и горизонтальной пластины (с).
а J в
с
Рис. 8.11. Векторные диаграммы для некоторых геологических моделей
8.4.2. Вертикальный градиент Для оценки глубины залегания намагниченных источников можно использовать совместный анализ наблюденного магнитного поля и его вертикальной производной. Если измерения выполнены протонным или квантовым магнитометрами, то для диполя можно написать упрощенное выражение
Дифференцируя данную формулу, получим
Заметим, что аномалия вертикального градиента от диполя изменяется пропорционально множителю Для тонкого пласта будем иметь аномалию
вертикальный градиент
Аномалия градиента от такого источника изменяется пропорционально
аномалия градиента будет равна
Данные формулы могут быть использованы для быстрого определения глубины залегания источников магнитного поля. Для диполя получим
для горизонтального цилиндра –
для края узкой вертикальной дайки –
и для аномалий в общем случае –
Способ прост, точность его – порядка несколько процентов. На практике он заключается в построении некой функции S, представляющей отношение Ta к вертикальному градиенту
Для определения вертикального градиента можно пользоваться известным интегралом Пуассона по расчету Та на высоту Δ h. В качестве среднего градиента можно использовать отношение
(Ta max – Ta max (D h)) / ∆ h. 8.4.3.Способ А. А. Логачева А.А.Логачев одним из первых предложил получать информацию о глубинах магнитных источников при помощи обработки с применением численного дифференцирования в различных плоскостях слаболокализованных максимумов аномальных кривых. На участках аномального графика в переходных зонах, т. е. слева и справа от максимума, дифференцированием вычисляются первые dZ / dx и вторые d 2 Z / dxdz производные. В точках перегиба исходной функции эти производные будут отмечаться экстремумами. На аномальном графике Za для вертикального пласта (7.2) можно видеть, что производная dZ / dx математически интерпретируется вертикальной плоскостью или линией полюсов, вторая производная d 2 Z / dxdz – дипольной линией, совпадающей с ребром вертикального пласта. По кривым градиентов можно оценить глубину залегания особой точки и угол наклона границы раздела. Для определения параметров магнитного источника можно использовать формулы
Рис. 8.12. Определение глубины залегания пласта по производным: а – исходная кривая Z а и принцип вычисления
(8.24)
где (dZ / dx)∆ h max – амплитуда магнитной аномалии на исходном уровне, В случае, если мощность пласта приблизительно равна его глубине, то для определения глубины рекомендуется использовать вторые производные d 2 Z / dxdz. Таким образом, предложения А. А. Логачева позволяют полнее использовать имеющуюся на магнитограмме информацию.
Логарифмические палетки
При исследованиях на рудных месторождениях магниторазведка обычно применяется в комплексе с электроразведкой. В связи с этим при обработке и интерпретации результатов используются методы, применяемые в электроразведке. По измеренным аномалиям на билогарифмическом бланке‑бумаге строится аномальный график, который накладывается на специальную логарифмическую палетку. При сравнении практической кривой с кривой палетки определяют глубину аномального тела. Рассмотрим построение палетки на примере вертикального пласта неограниченного распространения в глубину. Согласно формуле
Z = 2 J (arctg
максимальную амплитуду аномалии можно вычислить по формуле
Z max = 2 J 2 arctg
Чтобы исключить зависимость амплитуды от J и b, возьмем отношение Z / Z max . Если обозначить
В точке х h =0 это отношение равно единице и его логарифм равен нулю. Принимая эту точку за начало координат, построим логарифмический график функции Z / Z max (рис.8.13). Совокупность графиков, полученных для различных Р, представляет собой логарифмическую палетку. Индексами графиков являются значения Р. Вертикальная линия при х h =1 служит для определения глубины h. Пусть по профилю проведены наблюдения с шагом Δх и получены результаты Z 0, Z 1, Z 2, Z 3, где Z 0 – максимальное значение аномалии. По относительным значениям Z 1 / Z 0 =1, Z 2 / Z 0, Z 3 / Z 0 … на билогарифмической бумаге строится график. Этот график накладывается на палетку с теоретическими графиками (масштабы должны быть одинаковыми), и по точке, полученной при пересечении этим графиком вертикальной линии, при x h =1, определяется глубина h.
Рис.8.13. Логарифмическая палетка для оценки глубины намагниченного тела
Логарифмические палетки рассчитаны и построены для оценки количественных параметров аномальных тел при вертикальной и косой намагниченности, вертикальных и наклонных слоев неограниченного распространения. Набор палеток составляет атлас. Для выбора палетки необходимо предположить форму и намагниченность тела. Эти данные могут быть взяты из априорной информации.
МЕТОДЫ ИСТОЛКОВАНИЯ МАГНИТНЫХ АНОМАЛИЙ
Обратные задачи магниторазведки относятся к классу неустойчивых задач, так как магнитное поле имеет интегральный характер, т.е. является суммарным эффектом от всех источников поля, обусловленных неоднородностью геологического разреза. В результате наблюдаемое магнитное поле может быть малочувствительным даже к большим изменениям источников поля, если их влияния взаимно компенсируются. Получается, что существуют распределения магнитных источников с их характеристиками, сильно отличающимися друг от друг, но их суммарный эффект создает близкие магнитные поля. Создаются условия для неустойчивости обратного интерпретационного процесса. Попытка решить точно обратную задачу с приближенными данными может привести к результату, сильно отличающемуся от истинного. Такая задача в математической теории относится к некорректно поставленным. Корректность задачи должна предполагать наличие таких условий: существование решения, его единственность и устойчивость. Задачи, решения которых не удовлетворяют какому-либо из перечисленных условий, считаются поставленными некорректно, а их решения не несущими в себе физического содержания. Однако в действительности большинство практических задач магниторазведки не могут удовлетворить всем этим классическим условиям. Условия корректности решения обратных задач уточнены А.Н.Тихоновым. Согласно А.Н.Тихонову, задача математической физики считается поставленной корректно, если: 1) априори известно, что ее решение существует для некоторого класса данных и принадлежит некоторому заданному множеству корректности М; 2) решение единственно в некотором классе данных и в классе решений, принадлежащих множеству корректности М; 3) бесконечно малым вариациям данных задачи, не выводящим решение за пределы множества корректности М, соответствуют бесконечно малые вариации решения. Выделение из множества решений нужного решения, обладающего свойствами компакта, основано на использовании дополнительной априорной информации: геологические данные, предопределяющие выбор класса моделей; ограничение области нахождения источников; ограничение параметров значений (по данным бурения). Под единственностью решения обратной задачи понимается возможность однозначного нахождения источников по заданному внешнему полю. Задача должна быть поставлена корректно, если известно, что решение принадлежит некоторому классу корректности, для которого условия единственности решения установлены. Обратная задача в магниторазведке относится к задачам распознавания, когда по заданному полю требуется определить изучаемый объект. Решение обратной задачи существует, если имеются характеристики источников, подтверждающие наличие измеренного поля. Теоремы единственности доказываются для определенных классов моделей источников. Для однозначного представления в обратной задаче нескольких функций от нескольких переменных необходимо иметь измерения такого же количества функций от такого же числа переменных. В магниторазведке необходимо одновременно искать изменение намагниченности среды и распределение источников поля. Для однозначного решения обратной задачи для такого случая не хватает наблюденных данных. Поэтому при решении обратной задачи руководствуются критерием выбора приближенного решения из множества эквивалентных решений. Построение однозначной физико-геологической модели искомых объектов требует тщательного анализа возможных решений обратной задачи. Обратная задача в разведочной геофизике не может быть решена однозначно каким-либо одним методом. Эта неоднозначность или неопределенность решения имеет два аспекта. Один из них связан с выяснением геологической природы геофизических аномалий, другой – с получением оценок физических свойств и количественных параметров объектов: их формы, размеров, глубины и элементов залегания. Применительно к решению конкретной геологической задачи преобладающее значение может иметь либо качественная (определение природы аномалий), либо количественная (оценка геометрических и физических параметров объекта) неоднозначность, а чаще всего одновременно и та, и другая.
8.1.Качественная интерпретация аномалий магнитного поля Выбор методов интерпретации магнитных аномалий делается на основе изучения характера аномалий на картах магнитного поля (рис. 8.1). По их форме и направлению устанавливается простирание геологических объектов. Аномалии изометрической формы соответствуют, как правило, изометрическим в плане геологическим объектам, подобным шару или крутопадающему штокообразному телу типа вертикального кругового цилиндра. Линейно вытянутые аномалии обычно связаны со складками и телами платообразной формы. По интенсивности аномалий можно судить о вещественном составе изучаемых объектов, но для этого необходимо предварительно иметь данные о магнитных свойствах горных пород района исследования. Предварительная оценка глубины залегания верхней кромки намагниченных тел проводится по ширине аномалий, как правило, она не превышает размеры аномалии. С глубинными объектами обычно связаны широкие аномалии с пологими крыльями, и, наоборот, неглубоко залегающие тела характеризуются в магнитном поле более узкими, контрастными аномалиями с большим горизонтальным градиентом поля. По наличию и относительной величине минимумов, сопутствующих в некоторых случаях положительным аномалиям, можно качественно судить о распространении намагниченного объекта на глубину. Асимметрия графиков аномального поля свид
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 643; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.70.108 (0.011 с.) |

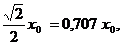 (8.1)
(8.1) ,
, 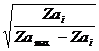 .
. 
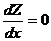 получим
получим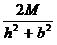 ;
;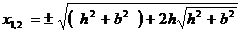 ;
;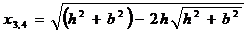 .
. ; в этом случае в точках х3 и х4, находящихся почти над краями горизонтального пласта, возникают максимумы Z (рис.7.11). С увеличением горизонтальной мощности пласта значение Z (0) над его центром убывает. Кривая Z пересекает ось х в точках х5,6 =
; в этом случае в точках х3 и х4, находящихся почти над краями горизонтального пласта, возникают максимумы Z (рис.7.11). С увеличением горизонтальной мощности пласта значение Z (0) над его центром убывает. Кривая Z пересекает ось х в точках х5,6 = 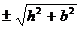 . Объединив представленные уравнения, получаем формулу для оценки глубины залегания горизонтальной пластины (пласта):
. Объединив представленные уравнения, получаем формулу для оценки глубины залегания горизонтальной пластины (пласта):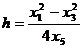 .
.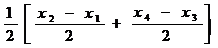 . (8.8)
. (8.8)
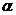 , (8.9)
, (8.9)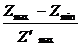
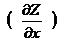 max.
max. 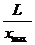

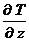 – это вектор, направленный вниз, а градиент
– это вектор, направленный вниз, а градиент 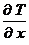 – это горизонтальный вектор. Суммарный полный вектор Т будет соответствовать точке взятия на профиле исходных отсчетов.
– это горизонтальный вектор. Суммарный полный вектор Т будет соответствовать точке взятия на профиле исходных отсчетов.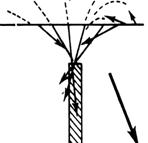
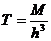 .
. 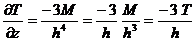 . (8.16)
. (8.16)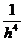 , а аномалии полного вектора Т – пропорционально
, а аномалии полного вектора Т – пропорционально 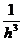 . Получаем, что вертикальный градиент полного вектора Т изменяется с расстоянием намного быстрее самой аномалии наблюденного поля и это его свойство может быть использовано для автоматической локализации магнитных аномалий.
. Получаем, что вертикальный градиент полного вектора Т изменяется с расстоянием намного быстрее самой аномалии наблюденного поля и это его свойство может быть использовано для автоматической локализации магнитных аномалий.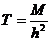 ,
, 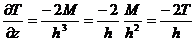 . (8.17)
. (8.17)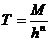 ,
,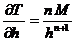 . (8.18)
. (8.18)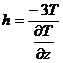 , (8.19)
, (8.19)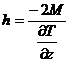 , (8.20)
, (8.20)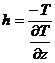 (8.21)
(8.21)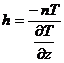 . (8.22)
. (8.22)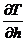 ,
,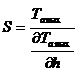 . (8.23)
. (8.23)



 ∂Z/∂ x(∆h)
2
∂Z/∂ x(∆h)
2  Δh
1
Δh
1  ∂Z/∂х
в
∂Z/∂х
в
 1
1 
 ∂2Z/∂ x ∂z
∂2Z/∂ x ∂z  c
c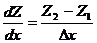 ; в – кривая dZ / dx на исходном уровне (1) и на высоте Δh (2); с – кривая d 2 Z / dxdz на исходном уровне (1) и на высоте пересчета Δh (2)
; в – кривая dZ / dx на исходном уровне (1) и на высоте Δh (2); с – кривая d 2 Z / dxdz на исходном уровне (1) и на высоте пересчета Δh (2)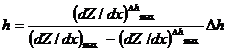 ,
, 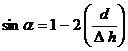 ,
,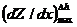 – амплитуда на уровне пересчета, расположенном на высоте ∆ h, а d – горизонтальное смещение максимумов указанных кривых. На рис. 8.12 показан ход представления производных различного порядка.
– амплитуда на уровне пересчета, расположенном на высоте ∆ h, а d – горизонтальное смещение максимумов указанных кривых. На рис. 8.12 показан ход представления производных различного порядка.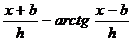 )
)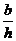 .
.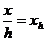 и
и 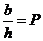 , то получим
, то получим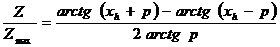 . (8.25)
. (8.25)