Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка глубины залегания намагниченных тел по градиентам различных порядковСодержание книги
Поиск на нашем сайте
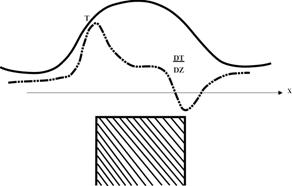
Для оценки глубины залегания намагниченных тел иногда представляют интерес не сами аномальные значения, а измерения или вычисления различных их градиентов. На практике чаще всего измеряют вертикальный градиент, а при интерпретации магнитных аномалий кроме его учитывают еще и сведения о горизонтальных градиентах. Градиенты можно измерять с помощью магнитометра, а также получать численными методами. Горизонтальный градиент магнитного поля вдоль какого-либо направления может легко быть вычислен по данным нужного профиля, тогда как вертикальный градиент по таким данным вычисляться не может. Полученные градиенты магнитного поля имеют несколько интересных свойств. Аномалии градиентов стремятся разложить сложные графики полного вектора Т на составные части и автоматически удаляют региональный магнитный фон, оставляя более ярко выраженные аномалии (рис. 8.9).
Рис.8.9. Локализация магнитных аномалий горизонтальным градиентом
Горизонтальные градиенты отображают величину уклона кривой изменения измеряемого элемента в какой-либо точке. Точные горизонтальные градиенты могут быть вычислены только в случае, когда аномалии имеют большую ширину, т.е. расстояние до источников больше расстояний между пикетами наблюдений. В случае изучения неглубоко залегающих магнитных объектов, когда аномалии полного вектора Т и его составляющих имеют большие амплитуды и быстрое затухание, необходимо учитывать, что отдельные измерения могут производиться в пространстве далеко друг от друга, поэтому нет смысла принимать их в расчет. Точность вычисления градиента в этих условиях значительно снижается.
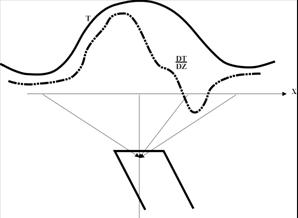
Векторные диаграммы Наблюденные или вычисленные градиенты Т можно использовать для экспрессной оценки глубины залегания намагниченных источников.
Рис.8.10. Построение векторных диаграмм
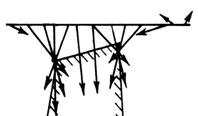
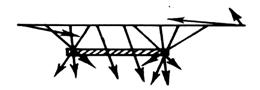
Для этого удобнее их представлять в векторной форме; градиент Векторное аномальное магнитное поле дает информацию об локальных особенностях геологического разреза, а места пересечения градиентных векторов показывают на наличие особых точек магнитных источников и их глубине залегания. Метод построения векторных диаграмм (рис.8.10) может быть достаточно эффективен при интерпретации магнитных аномалий над простыми геологическими структурами. На рис. 8.11 представлены векторные диаграммы для штокообразной модели (а), мощного пласта (в) и горизонтальной пластины (с).
а J в
с
Рис. 8.11. Векторные диаграммы для некоторых геологических моделей
8.4.2. Вертикальный градиент Для оценки глубины залегания намагниченных источников можно использовать совместный анализ наблюденного магнитного поля и его вертикальной производной. Если измерения выполнены протонным или квантовым магнитометрами, то для диполя можно написать упрощенное выражение
Дифференцируя данную формулу, получим
Заметим, что аномалия вертикального градиента от диполя изменяется пропорционально множителю Для тонкого пласта будем иметь аномалию
вертикальный градиент
Аномалия градиента от такого источника изменяется пропорционально
аномалия градиента будет равна
Данные формулы могут быть использованы для быстрого определения глубины залегания источников магнитного поля. Для диполя получим
для горизонтального цилиндра –
для края узкой вертикальной дайки –
и для аномалий в общем случае –
Способ прост, точность его – порядка несколько процентов. На практике он заключается в построении некой функции S, представляющей отношение Ta к вертикальному градиенту
Для определения вертикального градиента можно пользоваться известным интегралом Пуассона по расчету Та на высоту Δ h. В качестве среднего градиента можно использовать отношение
(Ta max – Ta max (D h)) / ∆ h. 8.4.3. Способ А. А. Логачева А.А.Логачев одним из первых предложил получать информацию о глубинах магнитных источников при помощи обработки с применением численного дифференцирования в различных плоскостях слаболокализованных максимумов аномальных кривых. На участках аномального графика в переходных зонах, т. е. слева и справа от максимума, дифференцированием вычисляются первые dZ / dx и вторые d 2 Z / dxdz производные. В точках перегиба исходной функции эти производные будут отмечаться экстремумами. На аномальном графике Za для вертикального пласта (7.2) можно видеть, что производная dZ / dx математически интерпретируется вертикальной плоскостью или линией полюсов, вторая производная d 2 Z / dxdz – дипольной линией, совпадающей с ребром вертикального пласта. По кривым градиентов можно оценить глубину залегания особой точки и угол наклона границы раздела. Для определения параметров магнитного источника можно использовать формулы
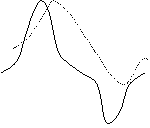
Рис. 8.12. Определение глубины залегания пласта по производным: а – исходная кривая Z а и принцип вычисления
(8.24)
где (dZ / dx)∆ h max – амплитуда магнитной аномалии на исходном уровне, В случае, если мощность пласта приблизительно равна его глубине, то для определения глубины рекомендуется использовать вторые производные d 2 Z / dxdz. Таким образом, предложения А. А. Логачева позволяют полнее использовать имеющуюся на магнитограмме информацию.
Логарифмические палетки
При исследованиях на рудных месторождениях магниторазведка обычно применяется в комплексе с электроразведкой. В связи с этим при обработке и интерпретации результатов используются методы, применяемые в электроразведке. По измеренным аномалиям на билогарифмическом бланке‑бумаге строится аномальный график, который накладывается на специальную логарифмическую палетку. При сравнении практической кривой с кривой палетки определяют глубину аномального тела. Рассмотрим построение палетки на примере вертикального пласта неограниченного распространения в глубину. Согласно формуле
Z = 2 J (arctg
максимальную амплитуду аномалии можно вычислить по формуле
Z max = 2 J 2 arctg
Чтобы исключить зависимость амплитуды от J и b, возьмем отношение Z / Z max . Если обозначить
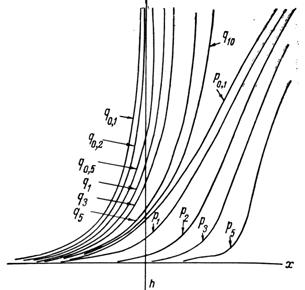
В точке х h =0 это отношение равно единице и его логарифм равен нулю. Принимая эту точку за начало координат, построим логарифмический график функции Z / Z max (рис.8.13). Совокупность графиков, полученных для различных Р, представляет собой логарифмическую палетку. Индексами графиков являются значения Р. Вертикальная линия при х h =1 служит для определения глубины h. Пусть по профилю проведены наблюдения с шагом Δх и получены результаты Z 0, Z 1, Z 2, Z 3, где Z 0 – максимальное значение аномалии. По относительным значениям Z 1 / Z 0 =1, Z 2 / Z 0, Z 3 / Z 0 … на билогарифмической бумаге строится график. Этот график накладывается на палетку с теоретическими графиками (масштабы должны быть одинаковыми), и по точке, полученной при пересечении этим графиком вертикальной линии, при x h =1, определяется глубина h.
Рис.8.13. Логарифмическая палетка для оценки глубины намагниченного тела
Логарифмические палетки рассчитаны и построены для оценки количественных параметров аномальных тел при вертикальной и косой намагниченности, вертикальных и наклонных слоев неограниченного распространения. Набор палеток составляет атлас. Для выбора палетки необходимо предположить форму и намагниченность тела. Эти данные могут быть взяты из априорной информации.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 504; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.64.210 (0.008 с.) |

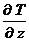 – это вектор, направленный вниз, а градиент
– это вектор, направленный вниз, а градиент 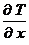 – это горизонтальный вектор. Суммарный полный вектор Т будет соответствовать точке взятия на профиле исходных отсчетов.
– это горизонтальный вектор. Суммарный полный вектор Т будет соответствовать точке взятия на профиле исходных отсчетов.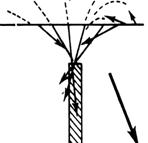
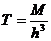 .
. 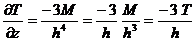 . (8.16)
. (8.16)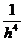 , а аномалии полного вектора Т – пропорционально
, а аномалии полного вектора Т – пропорционально 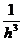 . Получаем, что вертикальный градиент полного вектора Т изменяется с расстоянием намного быстрее самой аномалии наблюденного поля и это его свойство может быть использовано для автоматической локализации магнитных аномалий.
. Получаем, что вертикальный градиент полного вектора Т изменяется с расстоянием намного быстрее самой аномалии наблюденного поля и это его свойство может быть использовано для автоматической локализации магнитных аномалий.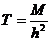 ,
, 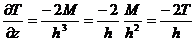 . (8.17)
. (8.17)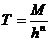 ,
,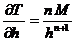 . (8.18)
. (8.18)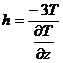 , (8.19)
, (8.19)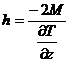 , (8.20)
, (8.20)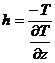 (8.21)
(8.21)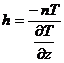 . (8.22)
. (8.22)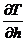 ,
,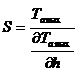 . (8.23)
. (8.23)



 ∂Z/∂ x(∆h)
2
∂Z/∂ x(∆h)
2  Δh
1
Δh
1  ∂Z/∂х
в
∂Z/∂х
в
 1
1 
 ∂2Z/∂ x ∂z
∂2Z/∂ x ∂z  c
c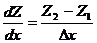 ; в – кривая dZ / dx на исходном уровне (1) и на высоте Δh (2); с – кривая d 2 Z / dxdz на исходном уровне (1) и на высоте пересчета Δh (2)
; в – кривая dZ / dx на исходном уровне (1) и на высоте Δh (2); с – кривая d 2 Z / dxdz на исходном уровне (1) и на высоте пересчета Δh (2)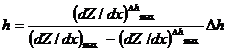 ,
, 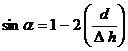 ,
,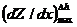 – амплитуда на уровне пересчета, расположенном на высоте ∆ h, а d – горизонтальное смещение максимумов указанных кривых. На рис. 8.12 показан ход представления производных различного порядка.
– амплитуда на уровне пересчета, расположенном на высоте ∆ h, а d – горизонтальное смещение максимумов указанных кривых. На рис. 8.12 показан ход представления производных различного порядка.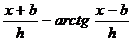 )
)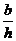 .
.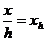 и
и 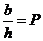 , то получим
, то получим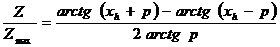 . (8.25)
. (8.25)