
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тонкий пласт, ограниченный по глубинеСодержание книги
Поиск на нашем сайте
При небольшой протяженности вертикально намагниченного пласта по глубине нижний край пласта, отрицательно намагниченный, будет оказывать заметное влияние на вид магнитной аномалии, форма кривых Z и Н будет несколько изменяться. В периферийных частях четкой положительной аномалии Z будут появляться слабые отрицательные поля (рис.8.4). Для пласта небольшой мощности будем иметь
над центром пласта получим
где m = 2 bl, M – магнитный момент сечения пласта, M = 2 b J 2 l = J S.
Рис. 8.4. Магнитное поле тонкого пласта, ограниченного по глубине
В этом случае определяется глубина залегания центра пласта h 0, площадь сечения S, половина вертикальной длины l и глубина до верхнего края пласта h 1:
h 1 =
где х1 – расстояние от центра аномалии до точки, где Z = 0, х2 – расстояние от центра аномалиидо минимума Zmin, х3 – расстояние от центра аномалии до точки, где Z = 0,5 Zmax, х4 – расстояние от центра аномалии до пересечения Z и H. 8.2.5. Мощный пласт
В случае мощного вертикально падающего пласта на симметричном аномальном графике Z а находят точки x 1/2 и x 1/4, в которых значения аномалий в 2 и 4 раза меньше, чем в начале координат. Для вычисления h и b используются формулы
(8.5)
Для определения J используется значение Za при х =0. В случае наклонного двухмерного пласта шириной 2в, намагниченного вертикально и бесконечно погруженного в глубину, согласно формулам (7.19, 7.20), кривые Z и Н имеют асимметричный вид. Графики могут быть разложены на составляющие в виде четной f (х) и нечетной φ(х) функций. Уравнение (7.19) перепишется в виде
Z = f (x)- φ (x).
Начало координат соответствует эпицентру верхней кромки пласта. Для определения местонахождения эпицентра используется тождество
Z (0) = / Zmax / - / Zmin /.
Далее по соотношениям (7.6) строятся четная и нечетная функции. Первая кривая f (х) с точностью до постоянного коэффициента соответствует кривой арктангенса:
f (x) = 2 J sin 2α arctg
Положение характерных точек совпадает с кривой вертикальной составляющей над вертикальным пластом большой мощности. Определение элементов залегания его можно найти по формулам (8.3, 8.4). Нечетная полученная новая кривая соответствует функции логарифма
φ (x) = J sin α cos α ln
ее вид совпадает с кривой горизонтальной составляющей напряженности магнитного поля над мощным вертикальным пластом. Она используется совместно с f (х) для определения угла наклона пласта по отношению функций f (х)/φ(х) для любой точки x профиля:
Интенсивность намагниченности J можно определить по максимальному значению четной функции. Описанные приемы разложения на две функции широко используются при решении обратной задачи по аномальным гафикам над контактами двух пород, сбросов и уступов. Горизонтальная пластина
Как следует из формул (7.21),кривая Z имеет пять точек экстремальных значений. По оценке Z (х=0) =
(8.7)
Точки х1,2 соответствуют Zmin, а точки х3, 4 имеют реальное значение при условии b > h
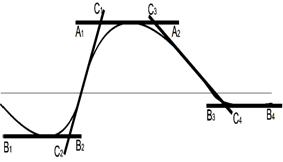
Если имеется кривая Н, то по аналогии можно найти связимежду ее характерными точками и элементами залегания пласта. 8. 3. Метод касательных Методы касательных основаны на аналитической зависимости ряда характерных точек кривой от параметров возмущающих объектов. В качестве основной исходной точки выбирают точку перегиба кривой исходного поля. Поэтому зависимость между координатами этой точки и параметрами возмущающих объектов выражается не через исходное поле, а через его производную в этой точке. В качестве дополнительных точек для составления системы уравнений выбираются любые другие точки: максимального и минимального значения поля, половины максимального значения; точки, где касательные к графику имеют наклон в два раза меньше, чем наклон основной касательной. Формулы для расчета глубин намагниченных объектов получаются из системы уравнений касательных, проведенных к точке перегиба и к какой-либо другой точке. Для каждой конкретной модели эти формулы будут иметь свои зависимости и могут быть использованы только для этого класса моделей. Способ касательных является эвристическим, т.е. получен без учета теории магниторазведки. Геофизик Ю.H. Грачев на примере аномальных графиков над шаром и круговым цилиндром по расстояниям между точками пересечения касательных, проведенных к характерным точкам заданной функции, нашел возможность определять глубину до поверхности (не до центра) магнитного источника. На рис.8.5 A 1 A 2 ‑ касательная в точке максимума, В1В2 и В3В4 – касательные в точках минимумов и C 1 C 2 и C 3 C 4 ‑ касательные в точках перегиба. Обозначая х1, х2, х3 и х4 ‑ абсциссы точек пересечения касательных, по разностям х2–х1 и х4–х3 предлагается находить глубину по следующей формуле:
h =
Рис.8.5. К определению глубины залегания магнитного тела способом касательных
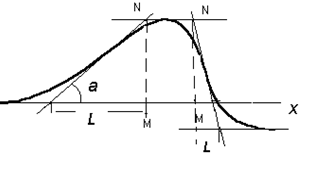
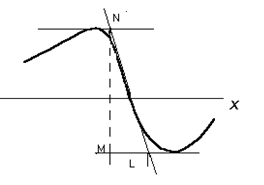
За рубежом этот метод называют методом наклона, так как он использует величину горизонтального градиента или наклон графика аномалии в точке перегиба. Метод основан на эмпирических наблюдениях, по данным которых установлен множитель К, являющийся коэффициентом пропорциональности между искомой глубиной и горизонтальным отрезком по оси Х = L, отсекаемым касательными. По графику аномальной кривой проводят касательные в точке положительного и отрицательного экстремума и в точке максимального градиента, т.е. в точке перегиба кривой (рис. 8.6). Полученная длина отрезка L в масштабе графика является функцией глубины и формы тела.
Рис.8.6. Модификации метода касательных
По изменению графика представим
L = MN / tg
где MN – наибольшая амплитуда, а Таблица 8.1
Значения глубины тела h в долях отрезка L, т. е. величины h: L для различных форм тел, приводятся в табл. 8.1. Рассмотрим практические методы определения глубины залегания некоторых тел.
8.3.1.Вертикальный контакт Глубину залегания верхней кромки h и намагниченности J определяют по формулам
h = L / К1,
и J = Z ´ max h / К 1 ´, (8.10) где L =
и Z ´ max =
Значения коэффициентов К1 и К2 зависят от относительной вертикальной мощности (l) пород контакта – сброса (l / h), определяемой по отношению 2 хэ: L, где х э – абсцисса максимума и минимума кривой. Значения величин, необходимых для определения h и J, приведены в табл.8.2.
Таблица 8.2
Определив h и l, находим глубину залегания нижней кромки тела: H = h + l. (8.11)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 142; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.20.205 (0.007 с.) |

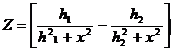 ,
,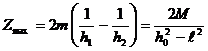 ,
,
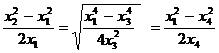 , (8.4)
, (8.4)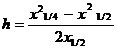 ,
,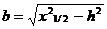 .
.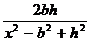 .
.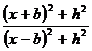 ,
,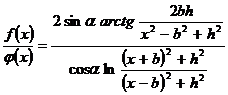 . (8.6)
. (8.6)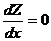 получим
получим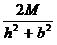 ;
;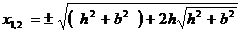 ;
;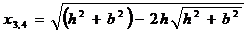 .
.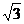 ; в этом случае в точках х3 и х4, находящихся почти над краями горизонтального пласта, возникают максимумы Z (рис.7.11). С увеличением горизонтальной мощности пласта значение Z (0) над его центром убывает. Кривая Z пересекает ось х в точках х5,6 =
; в этом случае в точках х3 и х4, находящихся почти над краями горизонтального пласта, возникают максимумы Z (рис.7.11). С увеличением горизонтальной мощности пласта значение Z (0) над его центром убывает. Кривая Z пересекает ось х в точках х5,6 = 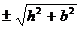 . Объединив представленные уравнения, получаем формулу для оценки глубины залегания горизонтальной пластины (пласта):
. Объединив представленные уравнения, получаем формулу для оценки глубины залегания горизонтальной пластины (пласта):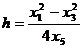 .
.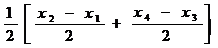 . (8.8)
. (8.8)
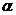 , (8.9)
, (8.9)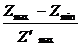
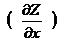 max.
max. 


