
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрические характеристики плоских сеченийСодержание книги
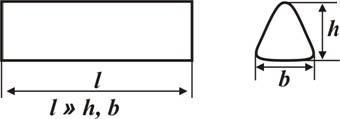
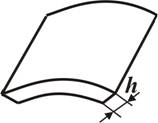
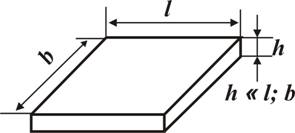
Поиск на нашем сайте Основные понятия В курсе «Сопротивление материалов» изучаются методы расчетов на прочность, жесткость и устойчивость элементов инженерных конструкций. Прочность – способность тела при нагружении его сопротивляться разрушению. Жесткость – способность тела при нагружении сопротивляться деформациям (изменениям размеров и его формы). Устойчивость – способность тела при нагружении сохранять первоначальную форму равновесия. Основные элементы инженерных конструкций, которые рассчитываются в курсе сопротивления материалов – это стержень (балка, рисунок 1а), оболочка (рисунок 1б) и пластина (рисунок 1в).
а)
б) в)
Рисунок 1
Рисунок 2
Для расчетов на прочность и жесткость необходимо знать внутренние силовые факторы, которые возникают в поперечных сечениях элементов конструкций под действием внешних нагрузок (рисунок 2). В общем случае в поперечном сечении может возникнуть шесть внутренних силовых факторов: Внутренние силовые факторы определяют методом сечений. По этому методу элемент конструкции мысленно разрезается сечением, в котором нужно определить внутренние силовые факторы, на две части. На поверхности сечения одной из частей проводят оси координат, на которые проектируют все внешние нагрузки, действующие на другую часть (рисунок 2).
Если в поперечном сечении действует только один внутренний силовой фактор, то такой вид нагружения поперечного сечения называют простым. Если в поперечном сечении действуют несколько внутренних силовых факторов, то такой вид нагружения называют сложным. К простым видам нагружения относятся растяжение-сжатие, когда в поперечном сечении действует только нормальная сила, сдвиг, когда в поперечном сечении действует только перерезывающая сила, кручение, когда действует только крутящий момент, и изгиб, когда действует только один изгибающий момент. В качестве критерия оценки прочности в сопротивлении материалов в основном используют напряжение, т.е., удельную силу (силу, приходящуюся на единицу площади). Полное напряжение в любой точке сечения (рисунок 3) – определяется по формуле где
Рисунок 3
Для оценки прочности используются составляющие полного напряжения: Расчеты на прочность ведутся по условиям прочности, которые при простых видах нагружения поперечного сечения (в нем возникают только нормальные или только касательные напряжения) имеют вид где
Жесткость оценивается по величине деформаций, возникающих при нагружении элемента конструкции. Расчеты на жесткость проводятся по условию жесткости, а на устойчивость – по условию устойчивости. На основании условий прочности, жесткости и устойчивости могут производиться три вида расчетов: проверочный (максимальные напряжения или деформации, возникающие в элементе конструкции, сравнивают с допускаемыми); проектировочный, или конструкторский (из этих условий определяют размеры элемента конструкции); на грузоподъемность (из этих условий определяют максимально допустимые нагрузки, которые можно приложить к конструкции). Конкретные примеры расчетов на прочность, жесткость и устойчивость элементов конструкций будут рассмотрены в соответствующих разделах пособия. Растяжение-сжатие Растяжение-сжатие – это такой вид нагружения поперечного сечения элемента конструкции (стержня), при котором в этом сечении возникает один внутренний силовой фактор – нормальная сила Условие прочности в этом случае имеет вид где Допускаемое напряжение где Для пластичных материалов, разрушающихся при больших пластических (остаточных) деформациях, за
Жесткость при растяжении-сжатии оценивается по абсолютной деформации стержня где Если по длине стержня N, E и F изменяются, а функция Если стержень состоит из n участков и по длине li каждого из их Ni, Fi, Ei постоянны, то полная абсолютная деформация определяется как алгебраическая сумма деформаций каждого из участков:
Рисунок 4
Пример 1. Стальной стержень находится под действием продольных сил и собственного веса (рисунок 4). Найти нормальные силы и напряжения в поперечных сечениях его, определить перемещения сечений АА и ВВ. Дано P =2000 H; a = 2 м; b = 3 м; c = 1 м; F = 20 см2; E = 20 ×105 МПа; объемный вес материала g = 78 кН/м3. Решение. При вычислениях за единицу длины принимаем мм, за единицу силы Н, учитывая при этом, что единица напряжения
Так как нормальные силы и напряжения по длине стержня непостоянны, то с целью определения опасного поперечного сечения – сечения, где напряжения принимают максимальные значения – лучше построить эпюры (графики) изменения нормальной силы и напряжения по длине стержня. Эпюры будем строить по участкам, применяя для определения нормальной силы метод сечений (раздел I), т.е., проектируя на продольную ось стержня все нагрузки, приложенные ниже поперечного сечения, в котором определяется нормальная сила. При этом значения растягивающих нормальных сил и напряжений будем брать со знаком «плюс», сжимающих – со знаком «минус». I участок: На этом участке нормальную (растягивающую) силу создает только собственный вес стержня:
Это уравнение прямой линии, и для построения эпюры его достаточно двух точек. При при По этим данным строить эпюру на участке I. Нормальное напряжение в поперечных сечениях I участка
При при II участок: На этом участке нормальную силу создают сила P, вес I-го (нижнего) участка G1, который для II-го участка будет внешней нагрузкой, и собственный вес участка II:
при при
Строим эпюру N. при при Строим эпюру III участок: На этом участке нормальную силу создают силы P и 2 P, вес нижних участков G1 и G2 и собственный вес участка III: при
при Строим эпюру N. при при Строим эпюру Перемещение концевого сечения АА будет складываться из абсолютных деформаций всех трех участков (см. выражение 2.5): Деформацию первого участка будет вызывать только собственный вес G1:
Деформацию второго участка вызывают сила P, вес I-го участка G1 и собственный вес участка II:
Деформацию III участка вызывают силы Р и 2Р, вес I-го и II-го участков и собственный вес:
В результате получаем:
Перемещение сечения ВВ будет состоять только из деформации III участка:
Знак «минус» говорит о том, что эта часть стержня укорачивается, т.е. сечение ВВ перемещается вверх.
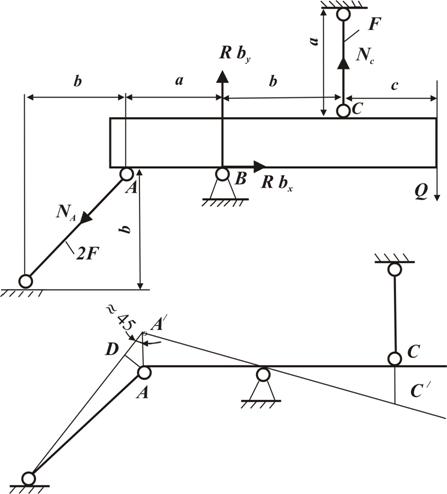
Пример 2. Абсолютно жесткий брус опирается на шарнирную неподвижную опору и прикреплен к двум стальным стержням при помощи шарниров (рисунок 5).
Рисунок 5
Требуется найти усилия и напряжения в стержнях, выразив их через силу Q. Найти допускаемую нагрузку [ Q ], приравняв большее из напряжений в двух стержнях к допускаемому Дано: Решение. Усилия в стержнях NA и NC будут равны реакциям шарниров А и С. Как известно из теоретической механики, реакции определяют из уравнений равновесия статики. Для плоской системы можно составить только три независимых уравнения статики. В нашей же системе – четыре неизвестных реакции: Так как реакции опоры
Отсюда
Для составления уравнений совместности деформаций рассмотрим нашу систему в деформированном состоянии. Ввиду малости деформаций удлинения стержня составят: Из пропорции следует: Подставим в это уравнение значения
Отсюда:
Решаем это уравнение совместно с уравнением статики (а):
Получаем: Определим напряжения в поперечных сечениях стрежней:
Так как напряжение
Отсюда допускаемая для конструкции нагрузка
Допускаемое напряжение согласно выражению (2.2)
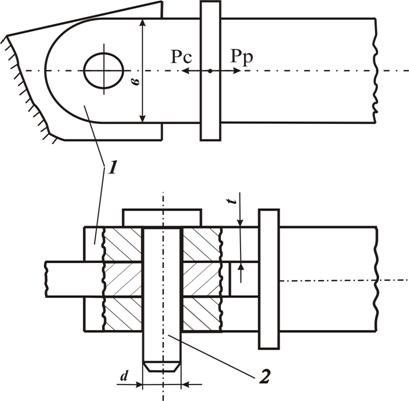
1 – щека гидроцилиндра 2 - палец Рисунок 6
Пример 3. Поверить прочность стальных щек гидроцилиндра (рисунок 6) механизма подъема рабочих органов глубокорыхлителя, если максимальное растягивающее усилие Решение. При вычислениях за единицу длины будем брать см. Максимальное растягивающее напряжение в поперечном сечении щеки, ослабленном отверстием:
Условие прочности выполняется. Сжимающие усилие и напряжение возникают в сечениях, не ослабленных отверстием:
Условие прочности выполняется. Сдвиг. Кручение Сдвиг Сдвиг – это такой вид нагружения поперечного сечения элемента конструкции, когда в этом сечении возникает один внутренний силовой фактор – перерезывающая сила где Пример. Проверить прочность стального пальца механизма подъема рабочих органов глубокорыхлителя (пример 3 раздел 2, рисунок 6), если допускаемое напряжение на сдвиг В качестве внешней нагрузки берем
Условие прочности выполняется. Кручение Кручение – это такой вид нагружения поперечного сечения элемента конструкции (вала), когда в этом сечении возникает один внутренний силовой фактор – крутящий момент. По форме поперечного сечения валы бывают круглые и некруглые. Будем рассматривать только кручение круглых валов. При анализе кручения, кроме крутящего момента В этом случае Крутящий момент вызывает в поперечном сечении вала касательные напряжения, и условие прочности в этом случае имеет вид где Для сплошного сечения где Для кольцевого сечения где Жесткость при кручении оценивается по углу закручивания где G – модуль упругости II рода (модуль сдвига), зависящий от материала и характеризующий его жесткость; Для сплошного сечения Для кольцевого сечения
Если вал состоит из n участков и по длине Пример 1. К стальному валу (рисунок 7) приложены известные внешние моменты:
Рисунок 7
Решение. Согласно условию задачи неизвестный момент Х найдем из условия, что угол закручивания по всей длине вала равен нулю. Для этого воспользуемся выражением (3.9). Так как вал имеет четыре участка, то
Для записи выражений крутящих моментов воспользуемся методом сечений (см. раздел 1). Суммируем все внешние моменты, приложенные справа от соответствующего поперечного сечения вала. С положительным знаком будет принимать крутящий момент, создаваемый внешним моментом, действующим против часовой стрелки (если смотреть с торца вала)
Подставим значения
Раскроем скобки и сделаем перегруппировку членов:
Отсюда
Знак «минус» говорит о том, что момент Х должен быть направлен в другую сторону, чем на приведенной в условии задачи схеме. В соответствии с этим перерисуем расчетную схему вала (рисунок7) и определим крутящие моменты. На первом участке По этим данным строим эпюру крутящих моментов. Подберем из условия прочности диаметр вала. Максимальный по абсолютной величине крутящий момент действует в поперечных сечениях I-го участка: Отсюда диаметр вала Для удобства вычислений переведем единицы измерения:
Ближайший больший стандартный диаметр – 45 мм. Его и берем для заданного вала. Для построения эпюры углов закручивания определим их на каждом из участков, взяв за единицу измерения крутящего момента
Эпюру углов закручивания начнем строить с левого конца вала, т.е. от заделки, где угол поворота сечения равен нулю. Углы поворота сечений относительно заделки
Строим эпюру углов закручивания. Угол концевого сечения равен нулю, что согласуется с условием задачи. Наибольший относительный угол закручивания будет там, где наибольший по абсолютной величине крутящий момент, т.е., на первом участке. На 1 м длины Или в градусах: Пример 2. Проверить прочность карданного вала валкового укладчика картофеля, если максимальная мощность, принимаемая валом Решение. Крутящий момент в поперечном сечении вала согласно выражению (3.2)
Максимальное касательное напряжение согласно выражениям (3.3) и (3.5)
Тогда
Условия прочности выполняются.
Прямой изгиб Прямым чистым изгибом называется такой вид нагружения поперечного сечения элемента конструкции (балки), при котором в этом сечении возникает один внутренний силовой фактор – изгибающий момент относительно одной из главных центральных осей инерции этого сечения. Изгибающий момент в поперечном сечении балки вызывает нормальные напряжения, и условие прочности в этом случае имеет вид где
Осевой момент сопротивления зависит от размеров и формы поперечного сечения и характеризует прочность балки при изгибе. Он берется относительно той главной центральной оси инерции сечения, относительно которой действует изгибающий момент. Для прямоугольного сечения где Для сплошного круглого сечения где Для кольцевого круглого сечения где Для стандартных прокатных профилей (швеллер, двутавр) Расчет на прочность ведется по наиболее опасному поперечному сечению балки, т.е. сечению, где возникает максимальный по абсолютной величине изгибающий момент, который обычно берут с эпюры (графика) изгибающих моментов, строящейся по длине балки. Так как в большинстве случаев у балок имеет место поперечный изгиб, а наряду с изгибающим моментом Если все внешние нагрузки находятся в одной плоскости, то величина перерезывающей силы в каком-либо поперечном сечении балки равна алгебраической сумме проекций всех внешних сил справа или слева от сечения на след плоскости этого сечения
Рисунок 10
Согласно правилу знаков (рисунок 10) перерезывающая сила считается положительной, если внешняя нагрузка слева от сечения направлена вверх или справа от сечения вниз. Изгибающий момент считается положительным, если под действием его балка изгибается вогнутостью вверх. Со стороны вогнутости продольные слои (волокна) балки находятся в сжатом состоянии, поэтому согласно правилу знаков изгибающий момент откладывается со стороны сжатых волокон балки. Перед построением эпюр там, где это необходимо, нужно определить реакции опор, а балку разбить на участки, границами которых являются точки приложения внешних нагрузок. При построении эпюр для контроля правильности имейте в виду следующее. Из правила определения Из дифференциальной зависимости между внутренними силовыми факторами при изгибе где следует, что согласно свойству производных положительная перерезывающая сила будет соответствовать возрастающему (алгебраически) изгибающему моменту, а отрицательная – убывающему. В том же месте, где Жесткость при изгибе оценивается по величине прогиба, т.е. перемещения центра тяжести поперечного сечения балки. Прогиб где
Если система, в которой опред
|
||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 375; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.21.161 (0.015 с.) |

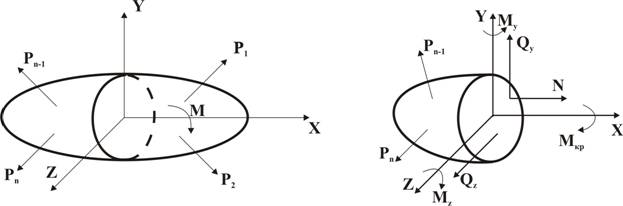
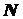 – нормальная сила;
– нормальная сила; 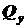 и
и 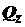 – перерезывающие силы;
– перерезывающие силы; 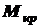 – крутящий момент;
– крутящий момент; 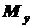 и
и 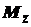 – изгибающие моменты.
– изгибающие моменты.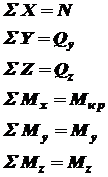 (1.1)
(1.1)
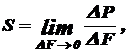 (1.2)
(1.2)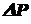 - внутреннее усилие, передаваемое через площадку
- внутреннее усилие, передаваемое через площадку 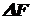 .
.
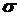 - нормальное напряжение;
- нормальное напряжение; 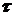 - касательное напряжение. Напряжения зависят от вида нагружения поперечного сечения элемента конструкции и величин внутренних силовых факторов и определяются в зависимости от них по соответствующим формулам.
- касательное напряжение. Напряжения зависят от вида нагружения поперечного сечения элемента конструкции и величин внутренних силовых факторов и определяются в зависимости от них по соответствующим формулам.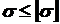 (1.3)
(1.3)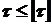 (1.4)
(1.4)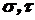 - максимальные напряжения, возникающие в процессе нагружения элемента конструкции;
- максимальные напряжения, возникающие в процессе нагружения элемента конструкции;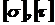 - допускаемые напряжения, при которых обеспечивается прочность материала.
- допускаемые напряжения, при которых обеспечивается прочность материала.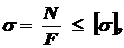 (2.1)
(2.1)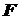 - площадь поперечного сечения стержня.
- площадь поперечного сечения стержня.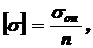 (2.2)
(2.2)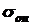 - опасное напряжение, при котором наступает предельное состояние материала;
- опасное напряжение, при котором наступает предельное состояние материала; 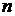 – коэффициент запаса прочности.
– коэффициент запаса прочности.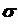 т – напряжение, при котором материал деформируется без заметного увеличения нагрузки (течет). Для хрупких материалов, разрушающихся при незначительных пластических деформациях и не имеющих заметного явления текучести, за
т – напряжение, при котором материал деформируется без заметного увеличения нагрузки (течет). Для хрупких материалов, разрушающихся при незначительных пластических деформациях и не имеющих заметного явления текучести, за 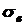 - напряжение, при котором начинается разрушение материала.
- напряжение, при котором начинается разрушение материала.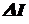 (удлинению или укорочению его). Если по длине стержня постоянны
(удлинению или укорочению его). Если по длине стержня постоянны 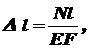 (2.3)
(2.3)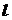 – длина стержня; Е – модуль упругости 1-го рода, зависящий от материала и характеризующий его жесткость.
– длина стержня; Е – модуль упругости 1-го рода, зависящий от материала и характеризующий его жесткость.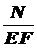 непрерывна, то
непрерывна, то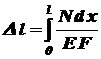 . (2.4)
. (2.4)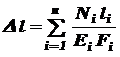 . (2.5)
. (2.5)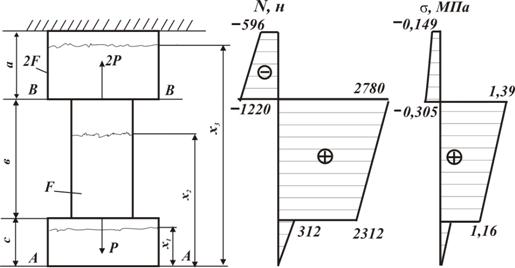
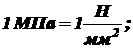
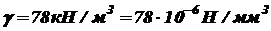 .
.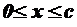 .
.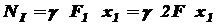 .
.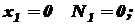
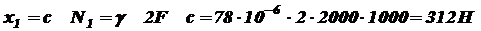 .
.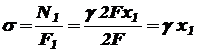 .
.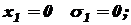
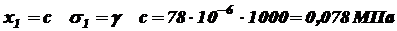 .
.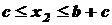 .
.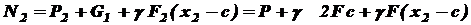 .
.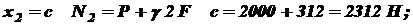
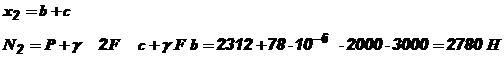
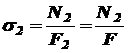 .
.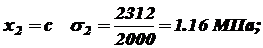
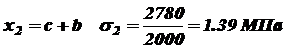
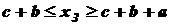 .
.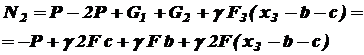
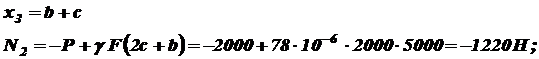
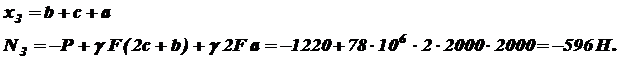
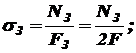
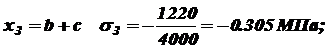
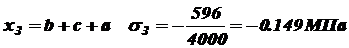
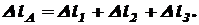
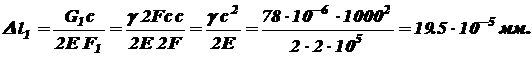
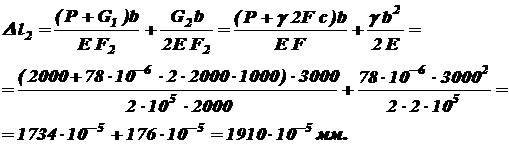
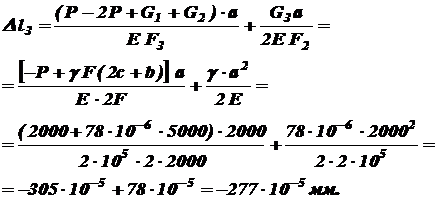
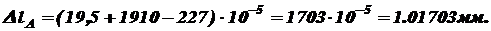
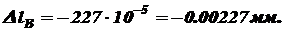
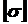 , если предел текучести материала
, если предел текучести материала 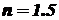 .
.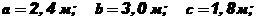
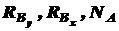 и
и 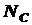 , т.е. для определения всех реакций не хватает одного уравнения. Такие системы называют статически неопределенными. Так как количество уравнений, которое необходимо составить в дополнение к уравнениям статики, чтобы вычислить все неизвестные реакции, определяет степень статической неопределимости системы, то наша конструкция будет один раз статически неопределима. Эти дополнительные уравнения описывают способности и возможности деформирования системы. Их называют уравнениями совместности деформаций.
, т.е. для определения всех реакций не хватает одного уравнения. Такие системы называют статически неопределенными. Так как количество уравнений, которое необходимо составить в дополнение к уравнениям статики, чтобы вычислить все неизвестные реакции, определяет степень статической неопределимости системы, то наша конструкция будет один раз статически неопределима. Эти дополнительные уравнения описывают способности и возможности деформирования системы. Их называют уравнениями совместности деформаций.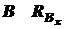 и
и 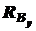 при расчете на прочность не нужны, то удобно составить одно уравнение статики, в которое бы не входили эти реакции. Этим уравнением будет сумма моментов всех сил относительно т. В:
при расчете на прочность не нужны, то удобно составить одно уравнение статики, в которое бы не входили эти реакции. Этим уравнением будет сумма моментов всех сил относительно т. В: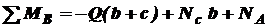
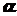
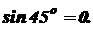
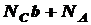
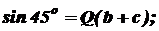

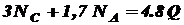 (а)
(а)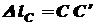 ,
, 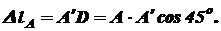
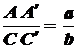
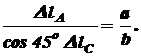
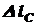 и
и 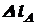 , которые получим согласно выражению (2.3):
, которые получим согласно выражению (2.3):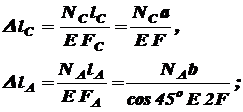
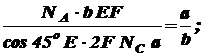
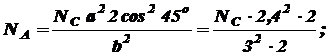
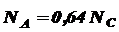 (б)
(б)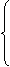
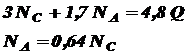
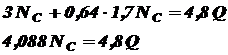
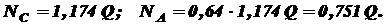
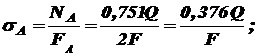
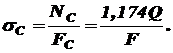
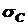 наибольшее, его и приравниваем согласно условию прочности (2.1) к допускаемому:
наибольшее, его и приравниваем согласно условию прочности (2.1) к допускаемому: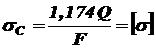 .
.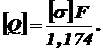
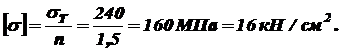
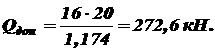
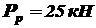 , а максимальное сжимающее
, а максимальное сжимающее 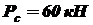 , допускаемое напряжение
, допускаемое напряжение 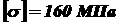 , ширина щек
, ширина щек 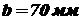 , толщина
, толщина 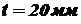 , диаметр пальца
, диаметр пальца 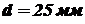 .
.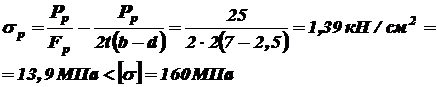
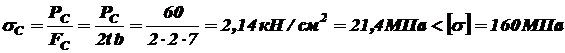
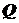 . Перерезывающая сила вызывает в поперечном сечении касательные напряжения, и условие прочности в этом случае имеет вид
. Перерезывающая сила вызывает в поперечном сечении касательные напряжения, и условие прочности в этом случае имеет вид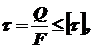 (3.1)
(3.1)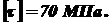
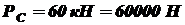 как наибольшую. Перерезывающая сила
как наибольшую. Перерезывающая сила 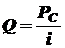 , где
, где 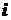 - число плоскостей сдвига, которое в данном случае равно 2. Площадь поперечного сечения пальца
- число плоскостей сдвига, которое в данном случае равно 2. Площадь поперечного сечения пальца 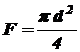 . С учетом этого максимальное касательное напряжение
. С учетом этого максимальное касательное напряжение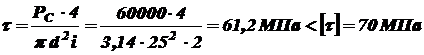
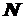 , передаваемая через вал, и частота вращения его n. Эти три параметра связаны между собой следующей зависимостью:
, передаваемая через вал, и частота вращения его n. Эти три параметра связаны между собой следующей зависимостью: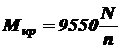 (3.2)
(3.2)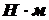 ,
, 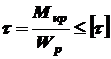 (3.3)
(3.3)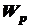 - полярный момент сопротивления поперечного сечения вала, характеризующий его прочность.
- полярный момент сопротивления поперечного сечения вала, характеризующий его прочность.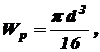 (3.4)
(3.4)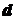 - диаметр вала.
- диаметр вала.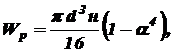 (3.5)
(3.5)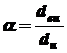 ;
; 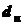 - наружный диаметр сечения;
- наружный диаметр сечения; 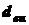 - внутренний диаметр сечения.
- внутренний диаметр сечения.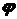 (углу поворота поперечных сечений вала друг относительно друга). Если на участке вала длиной l сечение постоянно, то
(углу поворота поперечных сечений вала друг относительно друга). Если на участке вала длиной l сечение постоянно, то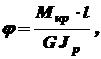 (3.6)
(3.6)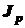 - полярный момент инерции поперечного сечения вала, характеризующий его жесткость.
- полярный момент инерции поперечного сечения вала, характеризующий его жесткость.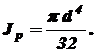 (3.7)
(3.7)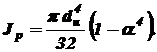 (3.8)
(3.8)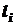 каждого из их
каждого из их 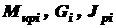 постоянны, то полный угол закручивания по всей длине вала определяется как алгебраическая сумма углов закручивания каждого из участков
постоянны, то полный угол закручивания по всей длине вала определяется как алгебраическая сумма углов закручивания каждого из участков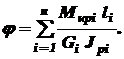 (3.9)
(3.9)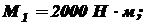
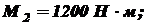
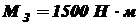 . Установить, при каком значении момента X угол поворота вправо концевого сечения равен нулю. При найденном значении X построить эпюру крутящих моментов. Из условия прочности определить диаметр вала, округлив его до ближайшего стандартно значения, если
. Установить, при каком значении момента X угол поворота вправо концевого сечения равен нулю. При найденном значении X построить эпюру крутящих моментов. Из условия прочности определить диаметр вала, округлив его до ближайшего стандартно значения, если 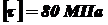 . Построить эпюру углов закручивания. Найти наибольший относительный угол закручивания (на 1 погонный метр длины), если a = 1,2 м, b = 1,4 м, c = 1,6 м, d = 1,8 м.
. Построить эпюру углов закручивания. Найти наибольший относительный угол закручивания (на 1 погонный метр длины), если a = 1,2 м, b = 1,4 м, c = 1,6 м, d = 1,8 м.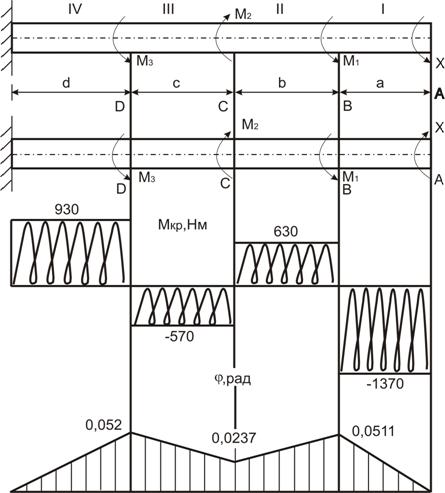
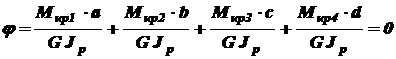
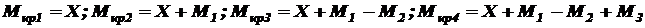
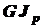 :
: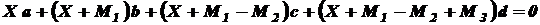
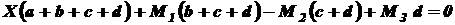
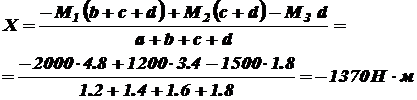
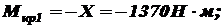 на втором участке
на втором участке 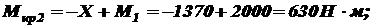 на третьем участке
на третьем участке 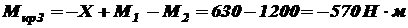 и на четвертом участке
и на четвертом участке 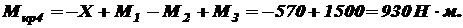
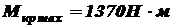 . Согласно выражениям (3.3) и (3.4)
. Согласно выражениям (3.3) и (3.4)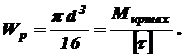
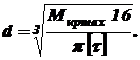
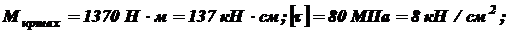
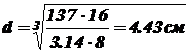
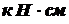 , длины – см, и учитывая, что для стали модуль сдвига
, длины – см, и учитывая, что для стали модуль сдвига 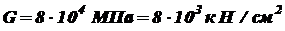 . Полярный момент инерции поперечного сечения
. Полярный момент инерции поперечного сечения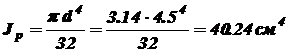 ;
;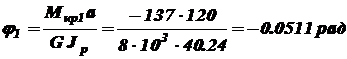 ;
;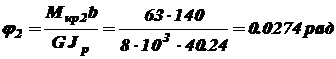 ;
;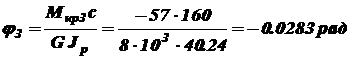 ;
;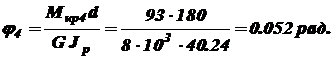
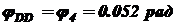 ;
;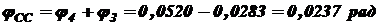 ;
;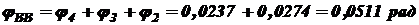 ;
;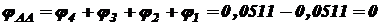 .
.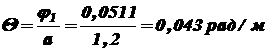
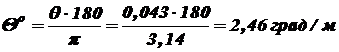 .
.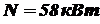 при частоте вращения его n = 800 об/мин. Вал имеет кольцевое поперечное сечение с наружным и внутренним диаметрами
при частоте вращения его n = 800 об/мин. Вал имеет кольцевое поперечное сечение с наружным и внутренним диаметрами 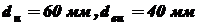 . Допускаемое напряжение для материала вала
. Допускаемое напряжение для материала вала 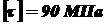 .
.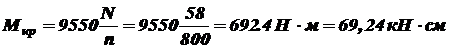 .
.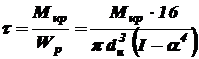
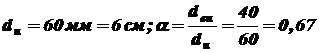 .
.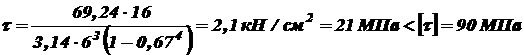
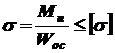 , (5.1)
, (5.1)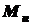 - изгибающий момент, возникающий в поперечном сечении балки;
- изгибающий момент, возникающий в поперечном сечении балки; - осевой момент сопротивления поперечного сечения балки.
- осевой момент сопротивления поперечного сечения балки.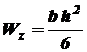 , (5.2)
, (5.2)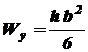 , (5.3)
, (5.3)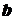 и
и 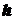 - длины сторон прямоугольника, параллельные соответственно главным осям инерции его
- длины сторон прямоугольника, параллельные соответственно главным осям инерции его 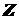 и
и 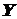 .
.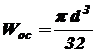 , (5.4)
, (5.4)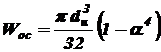 , (5.5)
, (5.5)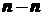 (рисунок 10), то есть на перпендикуляр к оси балки. Изгибающий момент при этом равен алгебраической сумме моментов всех внешних нагрузок справа или слева от сечения относительно точки пересечения плоскости сечения с осью балки.
(рисунок 10), то есть на перпендикуляр к оси балки. Изгибающий момент при этом равен алгебраической сумме моментов всех внешних нагрузок справа или слева от сечения относительно точки пересечения плоскости сечения с осью балки.
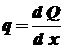 , (5.5)
, (5.5)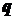 - интенсивность внешней распределенной нагрузки,
- интенсивность внешней распределенной нагрузки,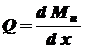 , (5.6)
, (5.6)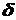 можно определить из интеграла Мора
можно определить из интеграла Мора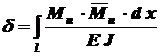 , (5.7)
, (5.7)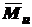 - изгибающий момент от единичной силы, приложенной в точке, перемещение которой нужно определить;
- изгибающий момент от единичной силы, приложенной в точке, перемещение которой нужно определить;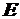 - модуль упругости 1-го рода;
- модуль упругости 1-го рода;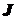 - осевой момент инерции поперечного сечения балки, взятый относительно той главной его оси, относительно которой действует изгибающий момент.
- осевой момент инерции поперечного сечения балки, взятый относительно той главной его оси, относительно которой действует изгибающий момент.


