
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Главные центральные моменты инерции некоторых сечений
Если сечение можно разбить на простые фигуры, то геометрические характеристики его определяют путем суммирования геометрических характеристик каждой отдельной фигуры относительно необходимых осей координат. Пример. Для сечения, состоящего из швеллера № 22а и равнобокого уголка
Рисунок 9 Решение. При вычислениях все размеры берем в см. Определение положения центра тяжести сечения. Используя выражения (4.7) и (4.8), определяем координаты центра тяжести сечения в системе осей
Площади сечений для швеллера (из таблицы ГОСТ8240 – 72) Координаты центров тяжести фигур:
Центр тяжести сечения должен находиться на линии, соединяющей центры тяжести двух составляющих его фигур (см. рисунок 9). Определение осевых и центробежных моментов инерции относительно центральных осей
Для швеллера (из таблицы ГОСТ8240 – 72):
Для уголка (из таблицы ГОСТ8509 – 72): Так как оси
Из таблицы ГОСТа:
Вычисляем
Определим положение главных центральных осей инерции и вычислим главные моменты инерции. По выражению (4.16)
что соответствует Угол Согласно выражению (4.17), главные центральные моменты инерции
Проверка. Так как главные моменты инерции экстремальны, то
При повороте осей координат сумма осевых моментов инерции должна оставаться постоянной
3724 + 262 = 3701 + 285;
Прямой изгиб Прямым чистым изгибом называется такой вид нагружения поперечного сечения элемента конструкции (балки), при котором в этом сечении возникает один внутренний силовой фактор – изгибающий момент относительно одной из главных центральных осей инерции этого сечения. Изгибающий момент в поперечном сечении балки вызывает нормальные напряжения, и условие прочности в этом случае имеет вид
где
Осевой момент сопротивления зависит от размеров и формы поперечного сечения и характеризует прочность балки при изгибе. Он берется относительно той главной центральной оси инерции сечения, относительно которой действует изгибающий момент. Для прямоугольного сечения где Для сплошного круглого сечения где Для кольцевого круглого сечения где Для стандартных прокатных профилей (швеллер, двутавр) Расчет на прочность ведется по наиболее опасному поперечному сечению балки, т.е. сечению, где возникает максимальный по абсолютной величине изгибающий момент, который обычно берут с эпюры (графика) изгибающих моментов, строящейся по длине балки. Так как в большинстве случаев у балок имеет место поперечный изгиб, а наряду с изгибающим моментом Если все внешние нагрузки находятся в одной плоскости, то величина перерезывающей силы в каком-либо поперечном сечении балки равна алгебраической сумме проекций всех внешних сил справа или слева от сечения на след плоскости этого сечения
Рисунок 10
Согласно правилу знаков (рисунок 10) перерезывающая сила считается положительной, если внешняя нагрузка слева от сечения направлена вверх или справа от сечения вниз. Изгибающий момент считается положительным, если под действием его балка изгибается вогнутостью вверх. Со стороны вогнутости продольные слои (волокна) балки находятся в сжатом состоянии, поэтому согласно правилу знаков изгибающий момент откладывается со стороны сжатых волокон балки. Перед построением эпюр там, где это необходимо, нужно определить реакции опор, а балку разбить на участки, границами которых являются точки приложения внешних нагрузок. При построении эпюр для контроля правильности имейте в виду следующее. Из правила определения Из дифференциальной зависимости между внутренними силовыми факторами при изгибе где следует, что согласно свойству производных положительная перерезывающая сила будет соответствовать возрастающему (алгебраически) изгибающему моменту, а отрицательная – убывающему. В том же месте, где Жесткость при изгибе оценивается по величине прогиба, т.е. перемещения центра тяжести поперечного сечения балки. Прогиб где
Если система, в которой определяется перемещение, состоит из прямолинейных участков и по длине участка
где
Пример 1. Дано: Решение. Определим реакцию опор
Проверим правильность определения реакций, спроектировав все силы на вертикальную ось
Разобьем балку на четыре участка.
Рисунок 11
Для упрощения выражений, определяющих I участок (слева): Уравнение перерезывающей силы Это уравнение прямой линии, и для построения эпюры достаточно двух точек. При По полученным данным строим эпюру Уравнение изгибающего момента Это уравнение параболы. При Так как II участок (слева): При Строим эпюру
При На этом участке Согласно выражению (5.6). При По этим данным строим эпюру При подходе к сечению справа начнем построение эпюр с IV участка. IV участок (справа): Строим эпюру При Строим эпюру III участок (справа): Строим эпюру При Строим эпюру В сечениях
Подберем для балки номер двутавра. Из условия прочности при изгибе (5.1) необходимый для обеспечения прочности осевой момент сопротивления С эпюры изгибающих моментов максимальный по абсолютной величине изгибающий момент В таблице ГОСТ 8239 – 72 ближайший больший Пример 2. Дано: Решение. Для этой балки при построении эпюр можно не определять реакции в заделке, если строить эпюры, подходя к сечению справа. При построении эпюр I участок (справа): Строим эпюру II участок (справа): При Строим эпюру
Рисунок 12 При В середине участка при
Согласно дифференциальным зависимостям (5.5) и (5.6) экстремум III участок (справа): При Строим эпюру
При При В середине участка при Строим эпюру IV участок (справа):
Строим эпюру
При При При Строим эпюру В сечении, где приложена сосредоточенная сила Определим диаметр балки, используя условие прочности (5.1) и выражение Отсюда С эпюры изгибающих моментов максимальной по абсолютной величине изгибающий момент Определим вертикальное перемещение конца балки, подставляя в формулу Симпсона (5.8) значения изгибающих моментов с эпюры изгибающих моментов
Для дерева
Пример 3. Из условия прочности при изгибе определить грузоподъемность передней оси валкового укладчика картофеля (рисунок 13). Ось имеет кольцевое поперечное сечение с наружным и внутренним диаметрами: Решение. В качестве расчетной схемы для оси можно принять двухопорную балку, нагруженную двумя сосредоточенными силами (рисунок 13). В этом случае реакции опор будут между собой равны Из условия прочности при изгибе (5.1) максимально допустимый изгибающий момент
Подставим значение Отсюда максимально допустимая нагрузка (грузоподъемность) для оси Подставляем из условия задачи:
Рисунок 13
Косой изгиб Косым изгибом называется такой изгиб, при котором плоскость действия изгибающего момента не совпадает с главной осью инерции поперечного сечения балки. Косой изгиб рассматривается как сумма двух прямых изгибов, т.е. суммарный изгибающий момент равен геометрической сумме моментов Напряжения в любой точке поперечного сечения балки определяется из выражения или где Наибольшие напряжения, по которым необходимо оценивать прочность балки, возникают в точках, наиболее удаленных от нейтральной линии сечения, на которой напряжения равны нулю. Нейтральная линия при косом изгибе представляет собой прямую, проходящую через начало координат. Угол Для симметричных сечений с выступающими углами (двутавр, прямоугольник) наибольшие напряжения возникают в угловых точках, наиболее удаленных от нейтральной линии. Условие прочности для балок с такими сечениями записывается в следующем виде: или где Полный прогиб балки при косом изгибе определяют как геометрическую сумму прогибов в направлении главных осей инерции поперечного сечения балки:
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 137; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.81.198 (0.131 с.) |
||||||||||||||||||||||||||||














 , определить положение главных центральных осей инерции и вычислить главные центральные моменты инерции (рисунок 9).
, определить положение главных центральных осей инерции и вычислить главные центральные моменты инерции (рисунок 9).
 и
и 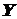 :
: ;
; .
. и уголка (из таблицы ГОСТ 8509 – 72)
и уголка (из таблицы ГОСТ 8509 – 72)  .
.
 ;
; ;
; .
. и
и  . Для этого используем формулы изменения геометрических характеристик при параллельном переносе осей координат (4.9) …(4.11), взяв за исходные центральные оси каждой фигуры:
. Для этого используем формулы изменения геометрических характеристик при параллельном переносе осей координат (4.9) …(4.11), взяв за исходные центральные оси каждой фигуры: ;
; ;
; .
. ;
; 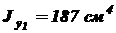 ;
;  , т.к. оси
, т.к. оси  и
и  для швеллера главные (оси симметрии);
для швеллера главные (оси симметрии); ;
; .
. .
. и
и  для уголка на являются главными, то определим центробежный момент инерции
для уголка на являются главными, то определим центробежный момент инерции  , используя выражение (4.14), взяв за исходные главные оси уголка
, используя выражение (4.14), взяв за исходные главные оси уголка  и
и  и учитывая, что
и учитывая, что  :
:


 , т.к. угол
, т.к. угол 
 отложен по часовой стрелке.
отложен по часовой стрелке. ;
; ;
; .
. ;
; ;
; .
. ,
, , а
, а  .
. положителен, откладываем его против часовой стрелки и проводим главные оси
положителен, откладываем его против часовой стрелки и проводим главные оси  и
и  .
.





 .
.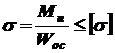 , (5.1)
, (5.1)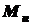 - изгибающий момент, возникающий в поперечном сечении балки;
- изгибающий момент, возникающий в поперечном сечении балки; - осевой момент сопротивления поперечного сечения балки.
- осевой момент сопротивления поперечного сечения балки.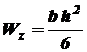 , (5.2)
, (5.2)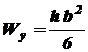 , (5.3)
, (5.3)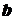 и
и 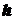 - длины сторон прямоугольника, параллельные соответственно главным осям инерции его
- длины сторон прямоугольника, параллельные соответственно главным осям инерции его 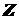 и
и 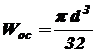 , (5.4)
, (5.4)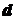 - диаметр круга.
- диаметр круга.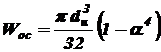 , (5.5)
, (5.5)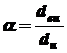 ;
; 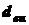 - внутренний диаметр;
- внутренний диаметр; 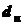 - наружный диаметр.
- наружный диаметр.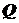 , то строят одновременно эпюры этих силовых факторов. Эпюры строятся под схемой каждой балки откладыванием в определенном масштабе в направлении оси ординат числовых значений перерезывающей силы
, то строят одновременно эпюры этих силовых факторов. Эпюры строятся под схемой каждой балки откладыванием в определенном масштабе в направлении оси ординат числовых значений перерезывающей силы 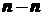 (рисунок 10), то есть на перпендикуляр к оси балки. Изгибающий момент при этом равен алгебраической сумме моментов всех внешних нагрузок справа или слева от сечения относительно точки пересечения плоскости сечения с осью балки.
(рисунок 10), то есть на перпендикуляр к оси балки. Изгибающий момент при этом равен алгебраической сумме моментов всех внешних нагрузок справа или слева от сечения относительно точки пересечения плоскости сечения с осью балки.
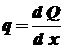 , (5.5)
, (5.5)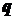 - интенсивность внешней распределенной нагрузки,
- интенсивность внешней распределенной нагрузки,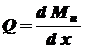 , (5.6)
, (5.6)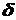 можно определить из интеграла Мора
можно определить из интеграла Мора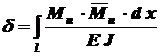 , (5.7)
, (5.7)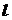 - длина балки;
- длина балки;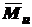 - изгибающий момент от единичной силы, приложенной в точке, перемещение которой нужно определить;
- изгибающий момент от единичной силы, приложенной в точке, перемещение которой нужно определить;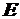 - модуль упругости 1-го рода;
- модуль упругости 1-го рода;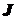 - осевой момент инерции поперечного сечения балки, взятый относительно той главной его оси, относительно которой действует изгибающий момент.
- осевой момент инерции поперечного сечения балки, взятый относительно той главной его оси, относительно которой действует изгибающий момент. , то интеграл может быть приближенно вычислен по формуле Симпсона:
, то интеграл может быть приближенно вычислен по формуле Симпсона: , (5.8)
, (5.8) - число участков;
- число участков;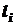 - длина участка;
- длина участка; - произведения изгибающих моментов от внешних нагрузок и единичных сил в начале, середине и конце каждого участка.
- произведения изгибающих моментов от внешних нагрузок и единичных сил в начале, середине и конце каждого участка. ,
,  ,
,  (рисунок11). Построить эпюры
(рисунок11). Построить эпюры 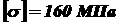 .
. и
и  из условий статики. В качестве уравнений статики возьмем суммы моментов относительно
из условий статики. В качестве уравнений статики возьмем суммы моментов относительно  и
и  :
: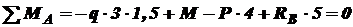 ;
; ;
;  .
. ;
; ;
;  .
. ;
; .
.
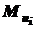 к сечениям на I и II участках, будем подходить слева, а на III и IV участках – справа, используя правило знаков (рисунок 10).
к сечениям на I и II участках, будем подходить слева, а на III и IV участках – справа, используя правило знаков (рисунок 10). .
. .
.
 ; при
; при 
 .
. на I участке.
на I участке. .
. ; при
; при 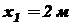
 .
. .
. .
. , при
, при 
 .
. .
. , при
, при  .
. ;
; .
.
 .
. .
. .
. .
.
 ; при
; при 

 .
. .
. .
.
 ; при
; при 
 .
. приложены сосредоточенные силы, и на эпюре перерезывающей силы есть скачки, а величину этих сил. В сечении
приложены сосредоточенные силы, и на эпюре перерезывающей силы есть скачки, а величину этих сил. В сечении 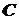 приложен сосредоточенный момент, и на эпюре изгибающих моментов есть скачок на его величину. В сечении
приложен сосредоточенный момент, и на эпюре изгибающих моментов есть скачок на его величину. В сечении  .
. . Согласно условию задачи
. Согласно условию задачи  .
. .
. . Этот двутавр берем для заданной балки.
. Этот двутавр берем для заданной балки. ,
,  ,
,  (рисунок 12). Построить эпюры
(рисунок 12). Построить эпюры  . Определить вертикальное перемещение свободного конца балки.
. Определить вертикальное перемещение свободного конца балки. .
.  ,
,  .
. .
. .
.
 ; при
; при 
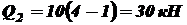 .
.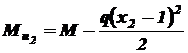

 ; при
; при  .
.
 .
. .
. .
.
 , при
, при 
 .
. .
. ;
; .
.
 .
. .
. .
.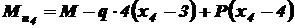 .
.
 ;
;
 ;
;
 .
. , перерезывающая сила делает скачок, а на эпюре изгибающих моментов есть перелом.
, перерезывающая сила делает скачок, а на эпюре изгибающих моментов есть перелом.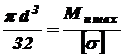 .
.
 . Из условия задачи
. Из условия задачи  .
. .
. (рисунок 12) в начале, середине и конце каждого участка:
(рисунок 12) в начале, середине и конце каждого участка:

 . Для круга осевой инерции (см. таблицу 4.1)
. Для круга осевой инерции (см. таблицу 4.1) ;
;
 ,
,  ,
,  . Допускаемое напряжение для материала оси
. Допускаемое напряжение для материала оси  .
. , а максимальный изгибающий момент с его эпюры
, а максимальный изгибающий момент с его эпюры .
. .
. .
. .
. ,
,  ,
,  ,
,  .
.
 .
.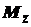 и
и 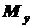 , действующих относительно главных осей инерции сечения
, действующих относительно главных осей инерции сечения  (6.1)
(6.1) , (6.2)
, (6.2) и
и  - координаты точки, в которой определяется напряжение;
- координаты точки, в которой определяется напряжение;  и
и 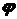 - угол между плоскостью действия изгибающего момента и главной осью
- угол между плоскостью действия изгибающего момента и главной осью 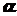 наклона этой линии к оси
наклона этой линии к оси  . (6.3)
. (6.3) (6.4)
(6.4) , (6.5)
, (6.5) и
и  - осевые моменты сопротивления поперечного сечения балки.
- осевые моменты сопротивления поперечного сечения балки.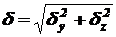 . (6.6)
. (6.6)


