
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методические указания к расчету на устойчивость сжатых стержней.Содержание книги
Поиск на нашем сайте
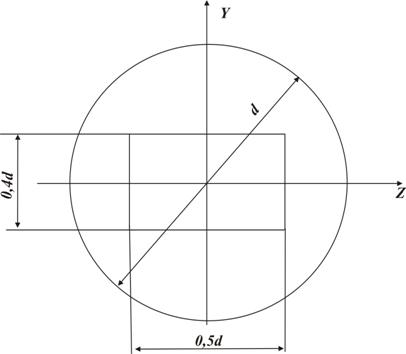
При определении критической силы и критического напряжения необходимо пользоваться либо формулами Эйлера (9.1) и (9.2), либо формулой Ясинского (9.5). Для этого необходимо сначала вычислить гибкость стержня При определении допускаемой нагрузки (грузоподъемности) для стержня или площади его поперечного сечения необходимо использовать условие устойчивости (9.6). При определении грузоподъемности необходимо вычислить гибкость стержня При определении площади поперечного сечения стержня задачу решают путем последовательных приближений, задаваясь различными значениями Пример 1. Определить размеры поперечного сечения (рисунок 18) стальной стойки длиной Выразим необходимые геометрические характеристики через размеры поперечного сечения, используя данные таблицы 4.1. Площадь сечения
Рисунок 18.
Минимальный осевой момент инерции сечения
Минимальный радиус инерции сечения согласно выражению (9.4)
Гибкость стойки (учитывая, что
Используя условие устойчивости (9.6), путем последовательных приближений определим размеры поперечного сечения стойки:
В первом приближении задаемся
Из таблицы 9.1 путем линейной интерполяции находим значение
Из условия устойчивости определим допускаемое усилие:
Полученное допускаемое усилие значительно меньше заданного Во втором приближении берем значение коэффициента продольного изгиба между
В этом случае стойка будет несколько недогружена. При Допускаемое напряжение на устойчивость
Сечение стойки недогружено на
что вполне допустимо. Определим величины критической нагрузки и коэффициента запаса устойчивости. Так как
Пример 2. Для колонны, состоящей из двух неравнобоких уголков 160´100´10 (рисунок 19), подобрать величину допускаемой нагрузки, если длина колонны 5 м, а допускаемое напряжение на сжатие Решение. Выпишем из таблиц ГОСТ 8510–72 и вычислим необходимые геометрические характеристики:
Рисунок 19
Площадь всего сечения Главные центральные моменты инерции сечения: относительно оси
относительно оси
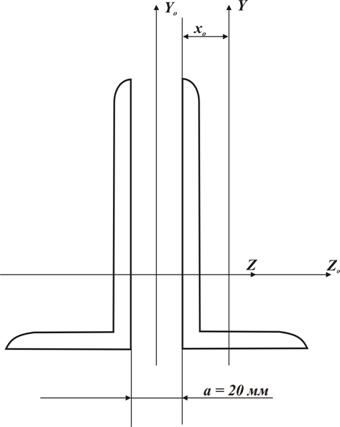
Следовательно, Минимальный радиус инерции сечения
Гибкость стержня при
Из условия устойчивости определим величину допускаемой нагрузки. Из таблицы 9.1 для
Определим величину критической силы и коэффициент запаса устойчивости. Так как
|
||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 130; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.215.30 (0.009 с.) |

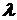 из выражения (9.3) и по ее величине определить, какую формулу нужно использовать.
из выражения (9.3) и по ее величине определить, какую формулу нужно использовать.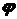 . Далее из условия устойчивости, используя допускаемое напряжение на сжатие, вычислить величину допускаемой нагрузки.
. Далее из условия устойчивости, используя допускаемое напряжение на сжатие, вычислить величину допускаемой нагрузки.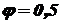 ), т.к. в этом случае в выражении условия устойчивости получается два неизвестных: площадь поперечного сечения
), т.к. в этом случае в выражении условия устойчивости получается два неизвестных: площадь поперечного сечения 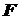 и коэффициент
и коэффициент 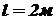 , если нагрузка, действующая на нее
, если нагрузка, действующая на нее 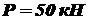 , а допускаемое напряжение при сжатии
, а допускаемое напряжение при сжатии 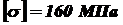 . Определить критическую силу и коэффициент запаса устойчивости. Один конец стойки защемлен, другой шарнирно опёрт (рисунок 17d).
. Определить критическую силу и коэффициент запаса устойчивости. Один конец стойки защемлен, другой шарнирно опёрт (рисунок 17d).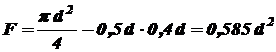
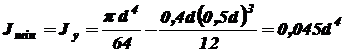 .
.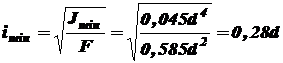 .
.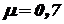 )
)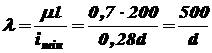 .
.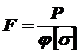 ;
;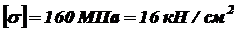 .
.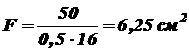 ;
;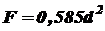 ;
; 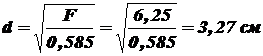 ;
;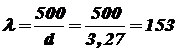 .
.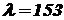 .
.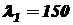 ;
; 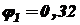 ;
; 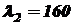 ;
; 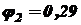 ;
;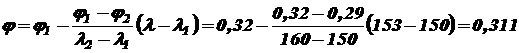 .
. .
.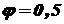 и
и 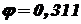 (несколько ближе к полученному значению
(несколько ближе к полученному значению 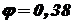 .
.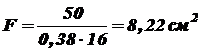
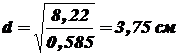 ;
;  ;
; 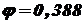 .
.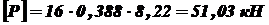 .
.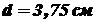 ,
, 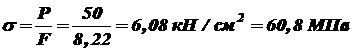 .
.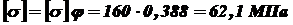 .
.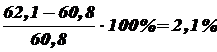 ,
,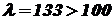 , тогда можно применить формулу Эйлера (9.1). Для подобранного значения
, тогда можно применить формулу Эйлера (9.1). Для подобранного значения 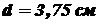 .
.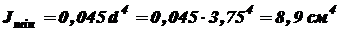 ;
;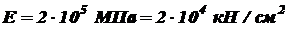 ;
;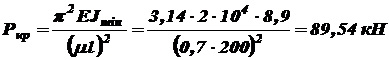 ;
;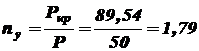 .
.
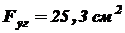 ;
; 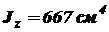 ;
; 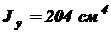 ;
; 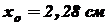 .
.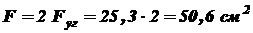 .
.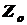
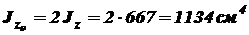 ;
;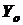 (используем формулу при параллельном переносе осей координат (4.10))
(используем формулу при параллельном переносе осей координат (4.10))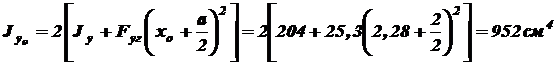 .
.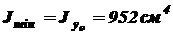 .
.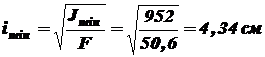 .
.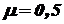 .
.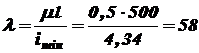 .
.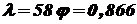 ;
;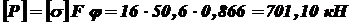 .
.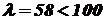 , тогда для определения критической силы используем формулу Ясинского (9.5). Для этого берем
, тогда для определения критической силы используем формулу Ясинского (9.5). Для этого берем 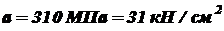 ;
; 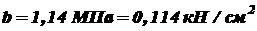 .
.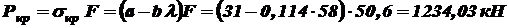 ;
;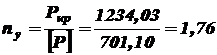 .
.


