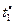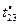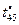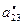Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Формирование стратегии вычислений
Пусть имеется модель задания, используемая в схемах 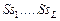 , каждая из которых , каждая из которых 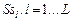 позволяет сформировать стратегию позволяет сформировать стратегию 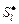 , условно оптимальную по критерию , условно оптимальную по критерию 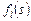 , входящему в вектор , входящему в вектор 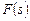 . По аналогии с (2.2.7) критерий . По аналогии с (2.2.7) критерий 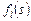 формирует частное бинарное отношение: формирует частное бинарное отношение:
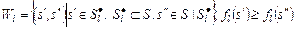 , (2.4.1) , (2.4.1)
где стратегия 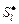 внутренне и внешне устойчива в модели выбора внутренне и внешне устойчива в модели выбора 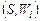 . .
Параллельная схема формирования стратегии для модели задания – семейство последовательных схем:
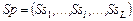 , , 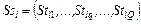 , , 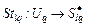 , (2.4.2) , (2.4.2)
где 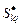 – множество условно оптимальных планов (2.2.5) для – множество условно оптимальных планов (2.2.5) для 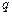 -й работы, выделенное из стратегии -й работы, выделенное из стратегии 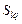 , полученной на этапе , полученной на этапе 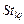 последовательной схемы последовательной схемы 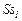 . .
При этом планы из 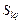 отбираются путем сравнения по отношению (2.4.1). Согласно (2.4.2) условно оптимальная по отбираются путем сравнения по отношению (2.4.1). Согласно (2.4.2) условно оптимальная по 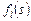 стратегия – семейство планов стратегия – семейство планов 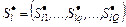 , а генерация , а генерация 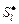 , , 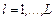 , может выполняться параллельно для всех критериев, входящих в , может выполняться параллельно для всех критериев, входящих в 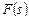 . .
Т е о р е м а 2. При формировании 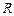 -оптимальной стратегии по параллельной схеме (2.4.2) имеет место следующее: -оптимальной стратегии по параллельной схеме (2.4.2) имеет место следующее:
– если
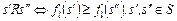 , , 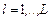 , (2.4.3) , (2.4.3)
то
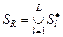 ; (2.4.4) ; (2.4.4)
– если отношение 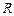 таково, что таково, что
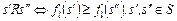 , , 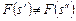 , (2.4.5) , (2.4.5)
то справедливо:
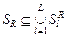 , (2.4.6) , (2.4.6)
где 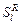 – множество оптимальных по – множество оптимальных по 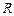 планов в модели выбора планов в модели выбора  ; ;
– если имеет место гомоморфизм 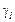 моделей выбора моделей выбора 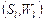 и и 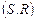 , такой что , такой что
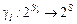 , , 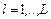 , , 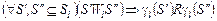 , (2.4.7) , (2.4.7)
то выполняется:
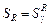 , (2.4.8) , (2.4.8)
где 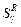 – множество оптимальных по – множество оптимальных по 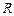 планов в модели выбора планов в модели выбора 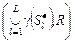 . .
Д о к а з а т е л ь с т в о т е о р е м ы 2. Рассмотрим следующие три случая.
Пусть имеет место (2.4.3). Поскольку 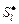 внешне устойчиво в модели выбора внешне устойчиво в модели выбора 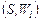 , то , то 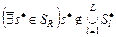 . Учитывая внутреннюю устойчивость . Учитывая внутреннюю устойчивость 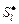 в в 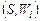 , приходим к (2.4.4). , приходим к (2.4.4).
Отношение 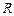 в (2.4.5) является отношением Парето и представляет собой асимметричную часть отношения (2.4.3). Предположим, что в (2.4.5) является отношением Парето и представляет собой асимметричную часть отношения (2.4.3). Предположим, что 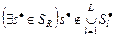 . По определению отношения Парето это означает, что . По определению отношения Парето это означает, что 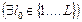 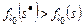 , где , где 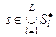 . Внешняя устойчивость . Внешняя устойчивость 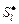 в модели выбора в модели выбора 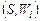 исключает существование такого плана. В силу того, что исключает существование такого плана. В силу того, что 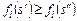 , , 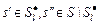 и и 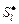 внутренне устойчиво в внутренне устойчиво в 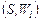 , получаем (2.4.6). , получаем (2.4.6).
Пусть определены гомоморфизмы (2.4.7) моделей выбора 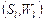 и и 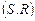 . С учетом свойства внешней устойчивости . С учетом свойства внешней устойчивости 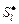 в модели выбора в модели выбора 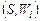 можно утверждать, что имеет место и гомоморфизм дополнений можно утверждать, что имеет место и гомоморфизм дополнений 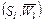 , , 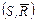 соответствующих моделей выбора: соответствующих моделей выбора:
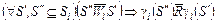 , ,
где 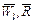 – дополнения отношений – дополнения отношений 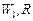 на множествах на множествах 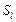 , , 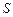 альтернатив соответственно, т.е. «нелучшие» планы в альтернатив соответственно, т.е. «нелучшие» планы в 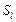 не могут быть представлены «лучшими» в не могут быть представлены «лучшими» в 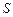 . В свою очередь, в соответствии с (2.4.7) «лучшие» в . В свою очередь, в соответствии с (2.4.7) «лучшие» в 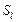 планы могут переходить в «лучшие» и в планы могут переходить в «лучшие» и в 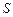 . Кроме этого, множество . Кроме этого, множество 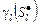 является внешне и внутренне устойчивым в модели выбора является внешне и внутренне устойчивым в модели выбора 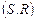 . Значит, . Значит, 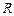 -оптимальную стратегию нужно отыскивать на семействе -оптимальную стратегию нужно отыскивать на семействе 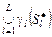 , откуда и следует (2.4.8). Теорема доказана. , откуда и следует (2.4.8). Теорема доказана.
Примеры формирования стратегии
П р и м е р 2.5.1. Рассмотрим применение параллельной схемы (2.4.2) к той же модели задания, что и в примере раздела 2.3 (см. рис. 2.1 и табл. 2.1).
Пусть отношение 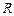 имеет вид (2.4.3), а векторный критерий включает функцию стоимости имеет вид (2.4.3), а векторный критерий включает функцию стоимости 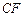 (2.1.5) и коэффициенты загрузки (2.1.5) и коэффициенты загрузки 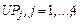 , базовых процессоров вида (2.1.6). Поскольку условные ветвления в графе задания отсутствуют (см. рис. 2.1), то , базовых процессоров вида (2.1.6). Поскольку условные ветвления в графе задания отсутствуют (см. рис. 2.1), то 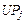 – отношение суммарного времени использования процессора типа – отношение суммарного времени использования процессора типа 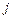 к сроку к сроку 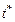 завершения выполнения задания. Стратегии, условно максимальные по критериям завершения выполнения задания. Стратегии, условно максимальные по критериям 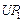 ; ; 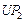 ; ; 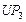 и и 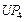 , представлены в табл. 2.2 соответственно вариантами: 4-7; 8, 9; 10, 11 и 12-14. По (2.4.4) , представлены в табл. 2.2 соответственно вариантами: 4-7; 8, 9; 10, 11 и 12-14. По (2.4.4) 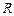 -оптимальная стратегия включает все 14 планов. Положим, динамика загрузки процессоров такова, что для задач -оптимальная стратегия включает все 14 планов. Положим, динамика загрузки процессоров такова, что для задач  может быть выделено не более трех единиц времени на первом и третьем процессорах (см. табл. 2.2). Метадиспетчер, просматривая совокупность планов, выбирает конкретный вариант распределения ресурсов, зависящий от фактической загрузки процессорных узлов. Тогда в качестве возможных вариантов распределения ресурсов метадиспетчер должен выбрать планы 1, 2, 4, 5, 12, 13. Конкретный же план должен быть оформлен в виде ресурсного запроса и реализован системой пакетной обработки в зависимости от состояния всех четырех процессоров и возможных времен запуска задач может быть выделено не более трех единиц времени на первом и третьем процессорах (см. табл. 2.2). Метадиспетчер, просматривая совокупность планов, выбирает конкретный вариант распределения ресурсов, зависящий от фактической загрузки процессорных узлов. Тогда в качестве возможных вариантов распределения ресурсов метадиспетчер должен выбрать планы 1, 2, 4, 5, 12, 13. Конкретный же план должен быть оформлен в виде ресурсного запроса и реализован системой пакетной обработки в зависимости от состояния всех четырех процессоров и возможных времен запуска задач 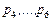 (см. табл. 2.2). В Парето-оптимальную стратегию также входят все планы, однако в общем случае должно выполняться (2.4.6), что иллюстрирует следующий пример. (см. табл. 2.2). В Парето-оптимальную стратегию также входят все планы, однако в общем случае должно выполняться (2.4.6), что иллюстрирует следующий пример.
П р и м е р 2.5.2. Пусть по параллельной схеме необходимо сформировать Парето-оптимальную стратегию распределения процессоров для модели, которой соответствует граф 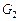 (см. рис. 2.1 и табл. 2.1). (см. рис. 2.1 и табл. 2.1).
Таблица 2.3
| П
Л
А
Н
| Длительность
| Назначение
| Критерии
| |
| 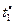
| 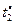
| 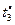
| 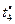
| 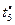
| 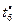
| 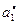
| 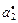
| 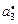
| 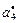
| 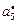
| 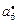
| 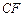
| 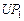
| 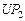
| 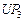
| 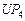
| | 1
| 2
| 3
| 3
| 4
| 4
| 3
| 1
| 1
| 3
| 2
| 4
| 1
| 39
| 0,40
| 0,20
| 0,15
| 0,20
| | 2
| 4
| 3
| 3
| 2
| 2
| 3
| 2
| 1
| 3
| 1
| 2
| 1
| 41
| 0,40
| 0,30
| 0,15
| 0
| | 3
| 4
| 3
| 3
| 3
| 3
| 2
| 2
| 1
| 3
| 1
| 3
| 1
| 40
| 0,40
| 0,20
| 0,30
| 0
| | 4
| 5
| 3
| 3
| 2
| 2
| 2
| 2
| 1
| 3
| 1
| 2
| 1
| 43
| 0,35
| 0,35
| 0,15
| 0
| | 5
| 2
| 3
| 3
| 2
| 2
| 5
| 1
| 1
| 3
| 1
| 2
| 1
| 43
| 0,60
| 0,10
| 0,15
| 0
| | 6
| 2
| 3
| 3
| 4
| 4
| 3
| 1
| 1
| 3
| 1
| 4
| 1
| 39
| 0,60
| 0
| 0,15
| 0,20
| | 7
| 2
| 3
| 3
| 5
| 5
| 2
| 1
| 1
| 3
| 1
| 4
| 1
| 41
| 0,60
| 0
| 0,15
| 0,25
| | 8
| 2
| 6
| 6
| 2
| 2
| 2
| 1
| 2
| 1
| 1
| 2
| 1
| 42
| 0,60
| 0,30
| 0
| 0
| | 9
| 4
| 3
| 3
| 2
| 2
| 3
| 1
| 1
| 3
| 1
| 2
| 1
| 41
| 0,60
| 0,10
| 0,15
| 0
| | 10
| 4
| 3
| 3
| 3
| 3
| 2
| 1
| 1
| 3
| 1
| 3
| 1
| 40
| 0,60
| 0
| 0,30
| 0
| | 11
| 4
| 4
| 4
| 2
| 2
| 2
| 1
| 1
| 4
| 1
| 2
| 1
| 41
| 0,60
| 0,10
| 0
| 0,20
| | 12
| 5
| 3
| 3
| 2
| 2
| 2
| 1
| 1
| 3
| 1
| 2
| 1
| 43
| 0,60
| 0,10
| 0,15
| 0
| | 13
| 2
| 6
| 6
| 2
| 2
| 2
| 1
| 2
| 4
| 1
| 2
| 1
| 43
| 0,30
| 0,40
| 0
| 0,30
| | 14
| 4
| 3
| 3
| 2
| 2
| 3
| 2
| 1
| 2
| 1
| 2
| 1
| 41
| 0,40
| 0,45
| 0
| 0
| | 15
| 4
| 3
| 3
| 3
| 3
| 2
| 2
| 1
| 2
| 1
| 2
| 1
| 40
| 0,40
| 0,50
| 0
| 0
| | 16
| 4
| 4
| 4
| 2
| 2
| 2
| 2
| 1
| 2
| 1
| 2
| 1
| 41
| 0,40
| 0,50
| 0
| 0
| | 17
| 5
| 3
| 3
| 2
| 2
| 2
| 2
| 1
| 2
| 1
| 2
| 1
| 43
| 0,35
| 0,50
| 0
| 0
| | 18
| 2
| 3
| 3
| 2
| 2
| 5
| 1
| 1
| 3
| 1
| 2
| 2
| 43
| 0,35
| 0,35
| 0,15
| 0
| | 19
| 2
| 3
| 3
| 4
| 4
| 3
| 1
| 1
| 3
| 2
| 3
| 1
| 39
| 0,40
| 0,20
| 0,35
| 0
| | 20
| 2
| 3
| 3
| 5
| 5
| 2
| 1
| 1
| 3
| 2
| 3
| 1
| 40
| 0,35
| 0,25
| 0,40
| 0
| | 21
| 2
| 6
| 6
| 2
| 2
| 2
| 1
| 2
| 3
| 1
| 2
| 1
| 42
| 0,30
| 0,40
| 0,30
| 0
| | 22
| 4
| 3
| 3
| 2
| 2
| 3
| 2
| 1
| 3
| 1
| 2
| 1
| 41
| 0,40
| 0,30
| 0,15
| 0
| | 23
| 4
| 3
| 3
| 3
| 3
| 2
| 2
| 1
| 3
| 1
| 3
| 1
| 40
| 0,40
| 0,20
| 0,30
| 0
| | 24
| 4
| 4
| 4
| 2
| 2
| 2
| 2
| 1
| 3
| 1
| 2
| 1
| 41
| 0,40
| 0,30
| 0,20
| 0
| | 25
| 5
| 3
| 3
| 2
| 2
| 2
| 2
| 1
| 3
| 1
| 2
| 1
| 43
| 0,35
| 0,35
| 0,15
| 0
| | 26
| 2
| 3
| 3
| 2
| 2
| 5
| 1
| 1
| 3
| 1
| 2
| 2
| 43
| 0,35
| 0,35
| 0,15
| 0
| | 27
| 2
| 3
| 3
| 4
| 4
| 3
| 1
| 1
| 3
| 2
| 4
| 1
| 39
| 0,40
| 0,20
| 0,15
| 0,20
| | 28
| 2
| 3
| 3
| 5
| 5
| 2
| 1
| 1
| 3
| 2
| 4
| 1
| 40
| 0,35
| 0,25
| 0,15
| 0,25
| | 29
| 2
| 6
| 6
| 2
| 2
| 2
| 1
| 2
| 4
| 1
| 2
| 1
| 42
| 0,30
| 0,40
| 0
| 0,30
| | 30
| 4
| 3
| 3
| 2
| 2
| 3
| 2
| 1
| 3
| 1
| 2
| 1
| 41
| 0,40
| 0,30
| 0,15
| 0
| | 31
| 4
| 3
| 3
| 3
| 3
| 2
| 2
| 1
| 3
| 1
| 3
| 1
| 40
| 0,40
| 0,20
| 0,30
| 0
| | 32
| 4
| 4
| 4
| 2
| 2
| 2
| 2
| 1
| 4
| 1
| 2
| 1
| 41
| 0,40
| 0,30
| 0
| 0,20
| | 33
| 5
| 3
| 3
| 2
| 2
| 2
| 2
| 1
| 3
| 1
| 2
| 1
| 43
| 0,35
| 0,35
| 0,15
| 0
| Отношение Парето формируется вектором критериев 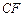 , , 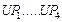 . Стратегия строится во всем диапазоне изменения длительности . Стратегия строится во всем диапазоне изменения длительности 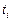 решения каждой из задач, а шаг изменения принимается не меньшим, чем нижняя граница диапазона (2.3.2). Остальные исходные условия те же, что и в предыдущих примерах. решения каждой из задач, а шаг изменения принимается не меньшим, чем нижняя граница диапазона (2.3.2). Остальные исходные условия те же, что и в предыдущих примерах.
Стратегии, условно оптимальные по критериям 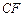 , , 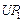 , , 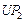 , , 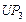 и и 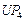 , представлены в табл. 2.3 планами 1-4, 5-12, 13-17, 18-25 и 26-33 соответственно. В Парето-оптимальную стратегию не попадают планы 2, 5, 12, 14, 16, 17, 22 и 30. Полученный результат согласуется с (2.4.6). , представлены в табл. 2.3 планами 1-4, 5-12, 13-17, 18-25 и 26-33 соответственно. В Парето-оптимальную стратегию не попадают планы 2, 5, 12, 14, 16, 17, 22 и 30. Полученный результат согласуется с (2.4.6).
2.6. Планы для разных моделей задания
Рассмотрим семейство параллельных схем, каждая из которых 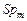 , , 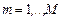 , позволяет сформировать условно оптимальные по критериям , позволяет сформировать условно оптимальные по критериям 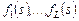 стратегии для соответствующей модели стратегии для соответствующей модели 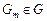 задания. Модели различаются уровнем параллелизма и степенью детализации задач (см. рис. 2.1), что важно для разрешения возможных конфликтов за разделяемый ресурс. Параллельная схема задания. Модели различаются уровнем параллелизма и степенью детализации задач (см. рис. 2.1), что важно для разрешения возможных конфликтов за разделяемый ресурс. Параллельная схема 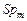 состоит из совокупности последовательных схем состоит из совокупности последовательных схем 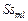 , с применением которых формируются стратегии , с применением которых формируются стратегии 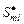 , условно оптимальные по соответствующему частному критерию , условно оптимальные по соответствующему частному критерию 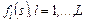 , , 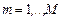 . .
Обобщенная схема формирования стратегии для множества 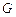 моделей задания – семейство схем вида: моделей задания – семейство схем вида:
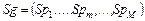 , , 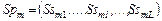 , , 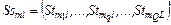 , , 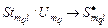 , (2.6.1) , (2.6.1)
где 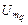 – подмножество задач модели – подмножество задач модели 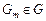 , составляющих , составляющих 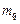 -ю работу; -ю работу; 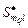 – множество условно оптимальных опорных планов, полученных на этапе – множество условно оптимальных опорных планов, полученных на этапе 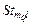 схемы схемы 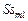 . .
Обозначим через 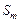 стратегию распределения ресурсов по параллельной схеме стратегию распределения ресурсов по параллельной схеме 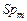 . Формальным обоснованием обобщенной схемы . Формальным обоснованием обобщенной схемы 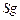 (2.6.1) служит следующее утверждение. (2.6.1) служит следующее утверждение.
Т е о р е м а 3. Положим, 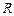 – квазипорядок на множестве – квазипорядок на множестве 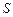 опорных планов, формируемых по обобщенной схеме опорных планов, формируемых по обобщенной схеме 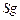 , в которой каждая из параллельных схем , в которой каждая из параллельных схем 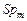 реализует модель выбора реализует модель выбора 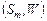 , где , где 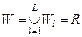 , а , а 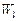 определяется согласно (2.4.1). Пусть определяется согласно (2.4.1). Пусть 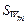 – непустая – непустая 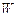 -оптимальная стратегия в модели выбора -оптимальная стратегия в модели выбора 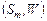 . Тогда имеет место: . Тогда имеет место:
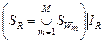 , (2.6.2) , (2.6.2)
где 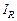 – отношение эквивалентности, порождаемое квазипорядком – отношение эквивалентности, порождаемое квазипорядком 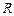 . .
Д о к а з а т е л ь с т в о т е о р е м ы 3. Рассмотрим семейство 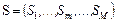 . Справедливо следующее: . Справедливо следующее:
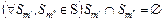 , (2.6.3) , (2.6.3)
поскольку 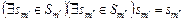 . Это объясняется различием структуры и параметров моделей . Это объясняется различием структуры и параметров моделей 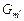 и и 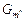 задания в схемах задания в схемах 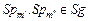 . .
Далее, имеет место
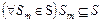 , , 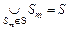 . (2.6.4) . (2.6.4)
Из (2.6.3) и (2.6.4) следует, что квазипорядок 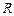 порождает отношение порождает отношение 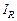 эквивалентности, которое задает разбиение эквивалентности, которое задает разбиение 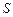 на классы на классы  , соответствующие параллельным схемам , соответствующие параллельным схемам 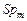 , , 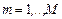 . .
Обозначим: 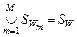 . Можно утверждать, что . Можно утверждать, что 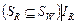 , поскольку , поскольку 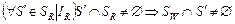 . Кроме этого, . Кроме этого, 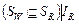 , поскольку , поскольку 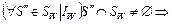 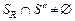 и и 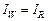 , где , где 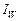 – отношение эквивалентности, порождаемое квазипорядком – отношение эквивалентности, порождаемое квазипорядком 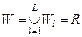 . Однако при этом не исключено, что . Однако при этом не исключено, что 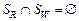 . Значит, справедливо (2.6.2), что и требовалось доказать. . Значит, справедливо (2.6.2), что и требовалось доказать.
2.7. Пример формирования планов для разных моделей задания
Рассмотрим применение обобщенной схемы декомпозиции (2.6.1) ко множеству моделей, которые структурно представлены графами 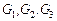 на рис. 2.1. Для модели на рис. 2.1. Для модели 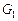 исходные условия те же, что и в примере 5.1, для моделей исходные условия те же, что и в примере 5.1, для моделей 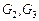 принимаются условия примера 5.2 того же раздела 2.5. Требуется построить принимаются условия примера 5.2 того же раздела 2.5. Требуется построить 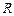 -оптимальную стратегию, где -оптимальную стратегию, где 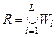 , а , а 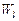 формируется одним из критериев формируется одним из критериев 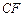 , , 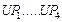 . В результате распределения ресурсов для модели . В результате распределения ресурсов для модели 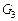 задачи задачи 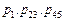 и и 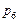 оказываются назначенными на один и тот же процессор первого типа. Следовательно, могут быть исключены затраты на обмены данными оказываются назначенными на один и тот же процессор первого типа. Следовательно, могут быть исключены затраты на обмены данными 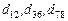 . Поскольку конфликтов между задачами обработки в этом случае возникнуть не может (см. рис. 2.1), то планирование, полученное до исключения процедур обмена, может быть пересмотрено. Результаты распределения процессоров приведены в табл. 2.4. Планы 1-6 в табл. 2.4 соответствуют стратегии, условно минимальной по . Поскольку конфликтов между задачами обработки в этом случае возникнуть не может (см. рис. 2.1), то планирование, полученное до исключения процедур обмена, может быть пересмотрено. Результаты распределения процессоров приведены в табл. 2.4. Планы 1-6 в табл. 2.4 соответствуют стратегии, условно минимальной по 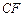 . При этом . При этом 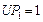 . Следовательно, нет смысла выполнять формирование условно максимальных планов по критериям . Следовательно, нет смысла выполнять формирование условно максимальных планов по критериям 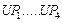 . Таким образом, . Таким образом, 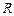 -оптимальная стратегия совпадает со стратегией, представленной в табл. 2.2, 2.3 и 2.4 для моделей -оптимальная стратегия совпадает со стратегией, представленной в табл. 2.2, 2.3 и 2.4 для моделей 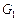 , , 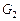 и и 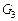 (см. рис. 2.1) с точностью до отношения (см. рис. 2.1) с точностью до отношения 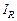 эквивалентности. эквивалентности.
Таблица 2.4
3. ПАКЕТНАЯ ОБРАБОТКА ЗАДАНИЙ В РАСПРЕДЕЛЕННЫХ ВЫЧИСЛИТЕЛЬНЫХ СРЕДАХ
|



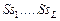 , каждая из которых
, каждая из которых 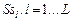 позволяет сформировать стратегию
позволяет сформировать стратегию 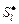 , условно оптимальную по критерию
, условно оптимальную по критерию 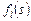 , входящему в вектор
, входящему в вектор 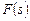 . По аналогии с (2.2.7) критерий
. По аналогии с (2.2.7) критерий 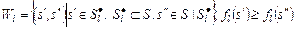 , (2.4.1)
, (2.4.1)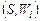 .
.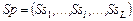 ,
, 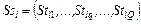 ,
, 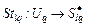 , (2.4.2)
, (2.4.2)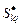 – множество условно оптимальных планов (2.2.5) для
– множество условно оптимальных планов (2.2.5) для 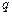 -й работы, выделенное из стратегии
-й работы, выделенное из стратегии 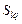 , полученной на этапе
, полученной на этапе 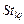 последовательной схемы
последовательной схемы 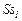 .
.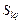 отбираются путем сравнения по отношению (2.4.1). Согласно (2.4.2) условно оптимальная по
отбираются путем сравнения по отношению (2.4.1). Согласно (2.4.2) условно оптимальная по 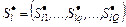 , а генерация
, а генерация 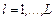 , может выполняться параллельно для всех критериев, входящих в
, может выполняться параллельно для всех критериев, входящих в 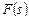 .
.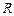 -оптимальной стратегии по параллельной схеме (2.4.2) имеет место следующее:
-оптимальной стратегии по параллельной схеме (2.4.2) имеет место следующее: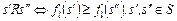 ,
, 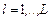 , (2.4.3)
, (2.4.3)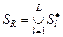 ; (2.4.4)
; (2.4.4)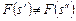 , (2.4.5)
, (2.4.5)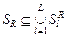 , (2.4.6)
, (2.4.6)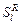 – множество оптимальных по
– множество оптимальных по  ;
;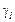 моделей выбора
моделей выбора 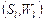 и
и 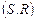 , такой что
, такой что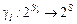 ,
, 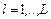 ,
, 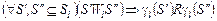 , (2.4.7)
, (2.4.7)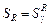 , (2.4.8)
, (2.4.8)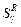 – множество оптимальных по
– множество оптимальных по 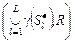 .
.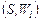 , то
, то 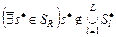 . Учитывая внутреннюю устойчивость
. Учитывая внутреннюю устойчивость 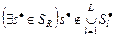 . По определению отношения Парето это означает, что
. По определению отношения Парето это означает, что 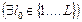
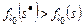 , где
, где 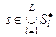 . Внешняя устойчивость
. Внешняя устойчивость 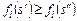 ,
, 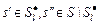 и
и 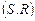 . С учетом свойства внешней устойчивости
. С учетом свойства внешней устойчивости 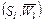 ,
, 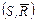 соответствующих моделей выбора:
соответствующих моделей выбора: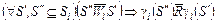 ,
,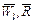 – дополнения отношений
– дополнения отношений 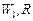 на множествах
на множествах 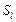 ,
, 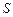 альтернатив соответственно, т.е. «нелучшие» планы в
альтернатив соответственно, т.е. «нелучшие» планы в 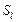 планы могут переходить в «лучшие» и в
планы могут переходить в «лучшие» и в 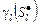 является внешне и внутренне устойчивым в модели выбора
является внешне и внутренне устойчивым в модели выбора 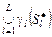 , откуда и следует (2.4.8). Теорема доказана.
, откуда и следует (2.4.8). Теорема доказана.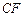 (2.1.5) и коэффициенты загрузки
(2.1.5) и коэффициенты загрузки 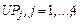 , базовых процессоров вида (2.1.6). Поскольку условные ветвления в графе задания отсутствуют (см. рис. 2.1), то
, базовых процессоров вида (2.1.6). Поскольку условные ветвления в графе задания отсутствуют (см. рис. 2.1), то 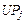 – отношение суммарного времени использования процессора типа
– отношение суммарного времени использования процессора типа 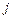 к сроку
к сроку 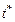 завершения выполнения задания. Стратегии, условно максимальные по критериям
завершения выполнения задания. Стратегии, условно максимальные по критериям 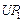 ;
; 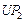 ;
; 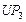 и
и 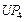 , представлены в табл. 2.2 соответственно вариантами: 4-7; 8, 9; 10, 11 и 12-14. По (2.4.4)
, представлены в табл. 2.2 соответственно вариантами: 4-7; 8, 9; 10, 11 и 12-14. По (2.4.4)  может быть выделено не более трех единиц времени на первом и третьем процессорах (см. табл. 2.2). Метадиспетчер, просматривая совокупность планов, выбирает конкретный вариант распределения ресурсов, зависящий от фактической загрузки процессорных узлов. Тогда в качестве возможных вариантов распределения ресурсов метадиспетчер должен выбрать планы 1, 2, 4, 5, 12, 13. Конкретный же план должен быть оформлен в виде ресурсного запроса и реализован системой пакетной обработки в зависимости от состояния всех четырех процессоров и возможных времен запуска задач
может быть выделено не более трех единиц времени на первом и третьем процессорах (см. табл. 2.2). Метадиспетчер, просматривая совокупность планов, выбирает конкретный вариант распределения ресурсов, зависящий от фактической загрузки процессорных узлов. Тогда в качестве возможных вариантов распределения ресурсов метадиспетчер должен выбрать планы 1, 2, 4, 5, 12, 13. Конкретный же план должен быть оформлен в виде ресурсного запроса и реализован системой пакетной обработки в зависимости от состояния всех четырех процессоров и возможных времен запуска задач 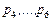 (см. табл. 2.2). В Парето-оптимальную стратегию также входят все планы, однако в общем случае должно выполняться (2.4.6), что иллюстрирует следующий пример.
(см. табл. 2.2). В Парето-оптимальную стратегию также входят все планы, однако в общем случае должно выполняться (2.4.6), что иллюстрирует следующий пример.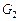 (см. рис. 2.1 и табл. 2.1).
(см. рис. 2.1 и табл. 2.1).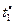
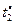
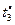
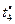
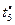
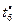
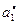
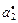
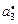
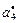
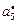
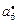
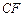
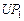
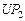
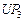
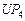
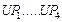 . Стратегия строится во всем диапазоне изменения длительности
. Стратегия строится во всем диапазоне изменения длительности 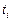 решения каждой из задач, а шаг изменения принимается не меньшим, чем нижняя граница диапазона (2.3.2). Остальные исходные условия те же, что и в предыдущих примерах.
решения каждой из задач, а шаг изменения принимается не меньшим, чем нижняя граница диапазона (2.3.2). Остальные исходные условия те же, что и в предыдущих примерах.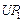 ,
, 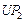 ,
, 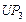 и
и 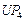 , представлены в табл. 2.3 планами 1-4, 5-12, 13-17, 18-25 и 26-33 соответственно. В Парето-оптимальную стратегию не попадают планы 2, 5, 12, 14, 16, 17, 22 и 30. Полученный результат согласуется с (2.4.6).
, представлены в табл. 2.3 планами 1-4, 5-12, 13-17, 18-25 и 26-33 соответственно. В Парето-оптимальную стратегию не попадают планы 2, 5, 12, 14, 16, 17, 22 и 30. Полученный результат согласуется с (2.4.6).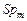 ,
, 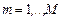 , позволяет сформировать условно оптимальные по критериям
, позволяет сформировать условно оптимальные по критериям 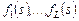 стратегии для соответствующей модели
стратегии для соответствующей модели 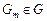 задания. Модели различаются уровнем параллелизма и степенью детализации задач (см. рис. 2.1), что важно для разрешения возможных конфликтов за разделяемый ресурс. Параллельная схема
задания. Модели различаются уровнем параллелизма и степенью детализации задач (см. рис. 2.1), что важно для разрешения возможных конфликтов за разделяемый ресурс. Параллельная схема 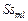 , с применением которых формируются стратегии
, с применением которых формируются стратегии 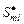 , условно оптимальные по соответствующему частному критерию
, условно оптимальные по соответствующему частному критерию 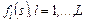 ,
, 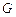 моделей задания – семейство схем вида:
моделей задания – семейство схем вида: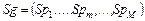 ,
, 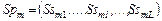 ,
, 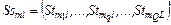 ,
, 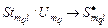 , (2.6.1)
, (2.6.1)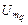 – подмножество задач модели
– подмножество задач модели 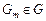 , составляющих
, составляющих 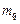 -ю работу;
-ю работу; 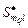 – множество условно оптимальных опорных планов, полученных на этапе
– множество условно оптимальных опорных планов, полученных на этапе 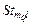 схемы
схемы 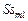 .
.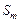 стратегию распределения ресурсов по параллельной схеме
стратегию распределения ресурсов по параллельной схеме 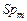 . Формальным обоснованием обобщенной схемы
. Формальным обоснованием обобщенной схемы 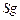 (2.6.1) служит следующее утверждение.
(2.6.1) служит следующее утверждение.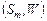 , где
, где 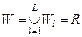 , а
, а 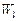 определяется согласно (2.4.1). Пусть
определяется согласно (2.4.1). Пусть 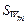 – непустая
– непустая 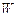 -оптимальная стратегия в модели выбора
-оптимальная стратегия в модели выбора 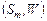 . Тогда имеет место:
. Тогда имеет место: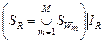 , (2.6.2)
, (2.6.2)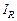 – отношение эквивалентности, порождаемое квазипорядком
– отношение эквивалентности, порождаемое квазипорядком 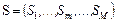 . Справедливо следующее:
. Справедливо следующее: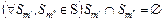 , (2.6.3)
, (2.6.3)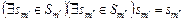 . Это объясняется различием структуры и параметров моделей
. Это объясняется различием структуры и параметров моделей 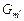 и
и 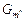 задания в схемах
задания в схемах 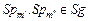 .
.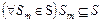 ,
, 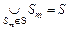 . (2.6.4)
. (2.6.4) , соответствующие параллельным схемам
, соответствующие параллельным схемам 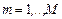 .
.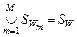 . Можно утверждать, что
. Можно утверждать, что 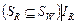 , поскольку
, поскольку 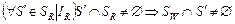 . Кроме этого,
. Кроме этого, 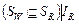 , поскольку
, поскольку 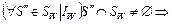
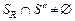 и
и 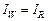 , где
, где 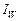 – отношение эквивалентности, порождаемое квазипорядком
– отношение эквивалентности, порождаемое квазипорядком 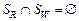 . Значит, справедливо (2.6.2), что и требовалось доказать.
. Значит, справедливо (2.6.2), что и требовалось доказать.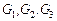 на рис. 2.1. Для модели
на рис. 2.1. Для модели 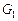 исходные условия те же, что и в примере 5.1, для моделей
исходные условия те же, что и в примере 5.1, для моделей 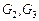 принимаются условия примера 5.2 того же раздела 2.5. Требуется построить
принимаются условия примера 5.2 того же раздела 2.5. Требуется построить 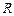 -оптимальную стратегию, где
-оптимальную стратегию, где 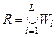 , а
, а 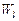 формируется одним из критериев
формируется одним из критериев 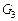 задачи
задачи 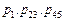 и
и 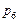 оказываются назначенными на один и тот же процессор первого типа. Следовательно, могут быть исключены затраты на обмены данными
оказываются назначенными на один и тот же процессор первого типа. Следовательно, могут быть исключены затраты на обмены данными 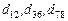 . Поскольку конфликтов между задачами обработки в этом случае возникнуть не может (см. рис. 2.1), то планирование, полученное до исключения процедур обмена, может быть пересмотрено. Результаты распределения процессоров приведены в табл. 2.4. Планы 1-6 в табл. 2.4 соответствуют стратегии, условно минимальной по
. Поскольку конфликтов между задачами обработки в этом случае возникнуть не может (см. рис. 2.1), то планирование, полученное до исключения процедур обмена, может быть пересмотрено. Результаты распределения процессоров приведены в табл. 2.4. Планы 1-6 в табл. 2.4 соответствуют стратегии, условно минимальной по 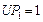 . Следовательно, нет смысла выполнять формирование условно максимальных планов по критериям
. Следовательно, нет смысла выполнять формирование условно максимальных планов по критериям 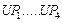 . Таким образом,
. Таким образом, 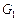 ,
, 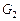 и
и