
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В.В. Топорков, Д.М. ЕмельяновСодержание книги
Поиск на нашем сайте
В.В. Топорков, Д.М. Емельянов
ПЛАНИРОВАНИЕ РАСПРЕДЕЛЕННЫХ ВЫЧИСЛЕНИЙ
УЧЕБНОЕ ПОСОБИЕ по курсу «Вычислительные системы» для студентов, обучающихся по направлению «Информатика и вычислительная техника»
Москва Издательство МЭИ 2018 УДК 621.398 ББК 32.97 Т 584 Утверждено учебным управлением МЭИ Подготовлено на кафедре вычислительной техники Рецензенты:, докт. техн. наук, проф. В.П. Климанов докт. техн. наук, проф. И.В. Огнев Топорков, В.В. Т 584 Планирование распределенных вычислений:учебное пособие / В.В. Топорков, Д.М. Емельянов. — М.: Издательство МЭИ, 2018. — 84 с. ISBN-978-5-7046-1870-6 Излагаются принципы планирования и обосновываются методы согласованного выделения ресурсов для организации вычислений в распределенных средах. Решение этих задач для выполнения сложных наборов заданий связывается с генерацией стратегий – семейств допустимых планов. Выбор конкретного плана зависит от характера событий, наступающих в распределенной среде и связанных, прежде всего, с загруженностью и доступностью вычислительных ресурсов. Представлены практические примеры, позволяющие глубже понять изложенный материал. Для студентов магистерской программы «Программный и проектный менеджмент», обучающихся по направлению «Информатика и вычислительная техника». —————— Учебное издание Топорков Виктор Васильевич Емельянов Дмитрий Михайлович ПЛАНИРОВАНИЕ РАСПРЕДЕЛЕННЫХ ВЫЧИСЛЕНИЙ Учебное пособие по курсу «Вычислительные системы» для студентов, обучающихся по направлению «Информатика и вычислительная техника»
Редактор Издательства ***. Компьютерная верстка ***. ¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾ Темплан издания МЭИ 2018, учебн. Подписано в печать Печать офсетная Формат 60×84/16 Физ. печ. л. 5,0 Тираж 200 экз. Изд. № 14у-066 Заказ ¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾ Оригинал-макет подготовлен в Издательстве МЭИ, 111250, г. Москва, Отпечатано в типографии Издательства МЭИ, 111250, г. Москва, ISBN-978-5-7046-1870-6 Ó Национальный исследовательский
ВВЕДЕНИЕ Организация вычислений в распределенных системах и средах, в отличие от составления расписаний в рамках известных моделей, обогащается таким важнейшим компонентом как управление ресурсами. Часто сложные наборы взаимосвязанных задач (задания) требуют согласованного выделения ресурсов (коаллокации) на нескольких вычислительных узлах. Каждый из узлов может находиться в автономном административном домене, представлять собой многомашинный или многопроцессорный комплекс, прохождением заданий в котором управляет своя локальная система пакетной обработки (СПО). Задание (исполняемые, входные и выходные файлы) часто принимается за единицу обработки в грид и замкнутых конфигурациях. Однако при этом его структура, как правило, не учитывается. Одно из немногих исключений применительно к параллельным вычислениям – планировщик в СПО Moab Cluster Suite, который допускает, что задание может состоять из параллельных задач, причем все задачи считаются однотипными в смысле требуемого вычислительного ресурса. В общем случае при согласованном выделении ресурсов необходимо учитывать и структуру задания, и разнотипность составляющих его задач. Методы и средства для согласованного распределения ресурсов при организации параллельных вычислений в замкнутых конфигурациях, например, в кластерах и архитектурах с распределенной разделяемой памятью, хорошо известны. Так, системы LL и СУППЗ реализуют назначение многопроцессорных заданий на множество однотипных процессоров; NQE и PBS допускают согласованное выделение процессоров и памяти; CODINE и LSF позволяют управлять ресурсами или выбирать их конфигурацию в неоднородных распределенных средах. В замкнутых конфигурациях предполагается полный контроль над всеми ресурсами, что не осуществимо в грид. Эффективное управление заданиями может быть реализовано на основе стратегий – комбинации различных алгоритмов и эвристик планирования с учетом многочисленных факторов и критериев: политики предоставления и администрирования ресурсов, динамичности состава, разнородности узлов и т.д. К факторам, влияющим на выбор стратегии согласованного распределения ресурсов, относятся степень загруженности узлов и наличие необходимых для вычислений данных, заставляющие использовать гибкую политику репликации и перемещения данных в среде, их упреждающее кэширование. Это и необходимость использования многокритериальных моделей, учитывающих интересы пользователей, владельцев ресурсов и политику предоставления ресурсов, принятую в той или иной виртуальной организации грид, а также механизмы ее реализации (экономические принципы или квоты). Выбор состава ресурсов зависит также от прогнозируемого времени выполнения пользовательской программы либо наличия контрольных сроков, обусловленных фактором реального времени. Таким образом, приходится рассматривать совокупность возможных сценариев в организации вычислений, а за их планированием в глобальной среде должно стоять нечто большее, чем один, пусть и очень совершенный алгоритм работы программы-планировщика. В организации распределенных вычислений можно выделить, по крайней мере, два взаимосвязанных аспекта. Один из них – планирование выполнения задач, входящих в задания. Другой аспект – такой подбор ресурсов для задания, когда принимаются во внимание информационно-логические связи между составляющими его задачами, их сложность, однотипность и т.д. Практически это дает возможность объединения под управлением одного менеджера ресурсов тех обрабатывающих узлов, которые сходны по архитектуре, составу, типу, политике администрирования. Кроме этого, учет структуры задания помогает сформировать базовый состав ресурсов в масштабируемых моделях планирования. В данном пособии описываются масштабируемая модель планирования и методы согласованного выделения ресурсов на основе стратегий, представляющих собой семейства возможных сценариев развития вычислений, конкретный вариант которых должен выбираться программой-планировщиком в зависимости от событий, наступающих в распределенной среде и связанных, главным образом, с занятием, освобождением и предварительным резервированием ресурсов. При распределении ресурсов масштабируемость обуславливает ряд существенных особенностей моделей планирования, отличающих их от известных подходов к составлению расписаний. Эти отличия объясняются, прежде всего, изменяемой потребностью задач в ресурсах и возможностью формирования многокритериальных стратегий вычислений. Реализация конкретного плана и фактическое выделение ресурсов осуществляются СПО заданий на основе ресурсного запроса пользователя, содержащего требования к типам, характеристикам ресурсов (памяти, процессорам), системному программному обеспечению и оформляемого, например, скриптом команды ввода задания qsub. Поэтому функции формирования и поддержки стратегий планирования должен выполнять своего рода метапланировщик – промежуточное звено между потоком заданий и системой пакетной обработки. В данном пособии рассматриваются различные схемы формирования стратегий, которые могут быть использованы при разработке инструментальных средств для систем и служб управления ресурсами распределенных вычислительных сред. Учебное пособие содержит введение, четыре раздела, перечень контрольных вопросов и список литературы. В первом разделе излагаются особенности управления работами в локально и глобально распределенных вычислительных средах, включая грид. Подробно описываются основные функции систем пакетной обработки заданий. Рассматривается семантика предоставления служб в грид, общие правила создания, именования и поиска экземпляров служб, связывание различных протоколов доступа к ресурсам. Во втором разделе рассматриваются задачи согласованного выделения ресурсов в распределенных вычислениях для сложно структурированных заданий. Дается формальное обоснование метода критических работ и описываются основные компоненты масштабируемой модели планирования. Приводятся примеры формирования планов по частным критериям и стратегий планирования на основе вектора критериев. Третий раздел посвящен планированию пакетов независимых заданий в виртуальных организациях грид. Неоднородность, динамичность состава и различная административная принадлежность вычислительных узлов, используемых совместно с их владельцами, существенно усложняют организацию распределенной обработки данных. В третьем разделе излагается подход к планированию пакетов независимых заданий на основе экономических принципов, принятых в виртуальной организации. Представлены практические примеры формирования оптимальной и эффективной комбинаций ресурсов, позволяющие глубже понять изложенный материал. В четвертом разделе излагаются основы теоретико-игрового подхода, которые могут быть применены к планированию распределенных вычислений в виртуальных организациях грид.
1. Управление ресурсами в распределенных средах Планирование вычислений в грид Можно выделить два основных подхода к планированию вычислений в глобальной среде. Один из них заключается в создании интерфейса между службами грид и локальными планировщиками, своего рода внешнего планировщика (метапланировщика) или метадиспетчера заданий. Другой подход основан на использовании брокеров – агентов уровня приложений, занимающихся поиском свободных ресурсов. Рассмотрим принципы глобального планирования на основе следующей модели (рис. 1.2). В этой модели внешний планировщик выполняет роль промежуточного звена между пользователями и множеством систем управления ресурсами на распределенных сайтах.
Рис. 1.2. Взаимодействие компонентов глобальной среды
Внешний планировщик в соответствии с некоторым алгоритмом определяет сайт, куда направляется поток заданий пользователя. Выбор сайта зависит от многих факторов: степени загруженности работами, наличия требуемых для вычислений данных и т.д. Эта информация может предоставляться локальными СПО. Для этого в них предусмотрена команда получения данных о текущем состоянии qstat. Однако информация, выдаваемая командой qstat, все-таки ориентирована на локальное управление ресурсами и, как правило, ее недостаточно для внешнего планирования. В преодолении этих трудностей может помочь механизм предварительного резервирования ресурсов, поддерживаемый рядом СПО. Сбор информации о состоянии локальных сайтов может опираться на информационную службу MDS системы Globus Toolkit. После того, как для задания выбран сайт, локальный планировщик (см. рис. 1.2) ставит это задание в очередь. Планировщик данных отвечает за доступ к данным на удаленных сайтах, перемещение и репликацию (тиражирование) данных. Репликация и перемещение данных в сочетании с внешним планированием является весьма действенным механизмом для управления заданиями в грид. В рассматриваемой модели (см. рис. 1.2) возможны различные сценарии взаимодействия пользователей, внешних планировщиков, локальных систем управления ресурсами и планировщиков данных. При этом эффективность планирования может оцениваться по совокупности критериев: использованию ресурсов, времени ответа на запросы пользователя и др. Вкратце на примере проекта AppLeS рассмотрим идею планирования на уровне приложений. Основная идея подхода состоит в том, что агенты-планировщики подбирают набор ресурсов для эффективного выполнения конкретного программного приложения. При этом у пользователя поддерживается иллюзия использования глобально распределенных вычислительных ресурсов исключительно в интересах его программы. Различные пользователи, естественно, пытаются оптимизировать свои приложения, разделяющие общие ресурсы, по совершенно различным критериям. Основная концепция проекта AppLeS – реализация заказного планировщика с учетом особенностей программного приложения. Эти особенности включают парадигму программирования, структуру данных, требования к памяти, модели обмена данными и т.д. Примерная структура агента-планировщика показана на рис. 1.3. Данные о распределенных ресурсах среды, особенностях приложения, пользовательских критериях производительности, моделях для оценки производительности и распределения ресурсов образуют так называемый информационный пул. Сбор информации о среде и прогнозирование загруженности ресурсов обеспечивается службой Network Weather Service. Четыре основные подсистемы агента, управляемые агентом-координатором, выполняют функции отбора той или иной комбинации ресурсов; планирования в соответствии с заданным пользователем критерием; взаимодействия с локальной системой управления ресурсами. Агент-координатор на основе оценки производительности отбирает лучший, с точки зрения пользователя, план и передает его через подсистему-исполнитель локальному планировщику в систему управления ресурсами. Нужно подчеркнуть, что оба рассмотренных подхода предполагают планирование приложений на основе динамично меняющейся информации о глобальной среде и позволяют реализовать различные сценарии управления ресурсами. Все это заставляет говорить не просто об алгоритме, а о стратегии планирования и распределения ресурсов, т.е. комбинации различных методов внешнего и локального планирования, размещения данных и т.д.
Рис. 1.3. Структура агента-планировщика
В разделе 2 данного пособия описывается один из возможных подходов к порождению стратегий вычислений по совокупности критериев, например, стоимости и коэффициентам загрузки (использованию) ресурсов. В заключение же заметим, что масштабируемые ресурсы и программное приложение можно рассматривать как своего рода единую среду, позволяющую оптимизировать динамические характеристики вычислительных процессов для создания эффективных распределенных программ.
2. Согласованное выделение ресурсов 2.1. Масштабируемая модель планирования Пусть
а б в Рис. 2.1. Структуры заданий в моделях Переход от графа
Таблица 2.1
Параметризованный граф Распределение
(2.1.1) где В (2.1.1) Пусть
Подчеркнем, что соотношения (2.1.1), (2.1.2) принципиально отличают масштабируемую модель планирования вычислений от традиционных моделей составления расписаний. Предположим, заданы ограничения на время выполнения отдельных задач и работ – последовательностей
где План, соответствующий варианту допустимого, согласно (2.1.2), (2.1.3), распределения (2.1.1), в критерии
Эффективность распределения ресурсов (2.1.1) будем оценивать по вектору Пример критерия – функция стоимости завершения обработки:
где Другой пример – коэффициент загрузки
где Пусть Постановка задачи распределения ресурсов, согласованного со структурой выполняемого задания, представленного множеством 2.2. Формирование планов по частному критерию Критической работой будем называть последовательность задач с наибольшей суммой априорных оценок длительности при использовании наилучшей комбинации ресурсов, которая содержит неназначенные задачи. Так, в графе Итеративное применение этой процедуры с разрешением конфликтов между параллельными задачами, конкурирующими за один и тот же ресурс, составляет суть метода критических работ. На основе этого метода, можно построить схему последовательного формирования планов вычислений для частного критерия эффективности использования ресурсов. Пусть
где В соответствии с методом критических работ условный экстремум функции
где Условно оптимальные длительность выполнения и назначение на ресурс при запасе
В (2.2.3) Условно оптимальным является план следующего вида:
Схема последовательного формирования планов для частной модели задания может быть определена как набор шагов
где Синтез стратегии Пусть частный критерий
где Будем называть Т е о р е м а 1. Стратегия Д о к а з а т е л ь с т в о т е о р е м ы 1. Пусть Благодаря внешней устойчивости Действительно,
где Рассмотрим наборы
Обозначим через | |||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: | |||||||||||||||||||||||||||||||||||||||||||||||||||||



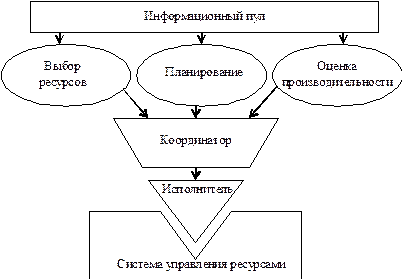
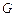 – множество параметризованных графов, представляющих задание с различными уровнем параллелизма и степенью детализации составляющих его частично упорядоченных задач. Отношение частичного порядка на совокупности
– множество параметризованных графов, представляющих задание с различными уровнем параллелизма и степенью детализации составляющих его частично упорядоченных задач. Отношение частичного порядка на совокупности 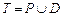 задач задается с помощью ориентированного бесконтурного графа, подмножество
задач задается с помощью ориентированного бесконтурного графа, подмножество 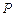 вершин которого соответствует задачам обработки и доступа к памяти, а подмножество
вершин которого соответствует задачам обработки и доступа к памяти, а подмножество 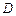 – процедурам обмена данными между задачами. Множество дуг графа представляет информационные и логические связи. На рис. 2.1 приведены примеры информационных графов
– процедурам обмена данными между задачами. Множество дуг графа представляет информационные и логические связи. На рис. 2.1 приведены примеры информационных графов 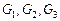 задания с различными уровнем параллелизма и детализацией задач: вершины
задания с различными уровнем параллелизма и детализацией задач: вершины 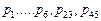 соответствуют обработке, а
соответствуют обработке, а 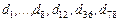 – передаче данных.
– передаче данных.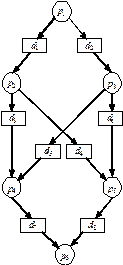
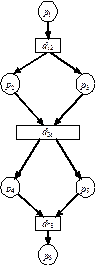
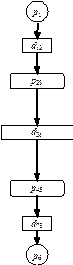
 (а),
(а), 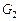 (б),
(б), 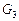 (в)
(в)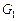 к графам
к графам 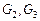 осуществляется путем укрупнения задач и понижения уровня параллелизма. Граф задания параметризуется априорными оценками длительности
осуществляется путем укрупнения задач и понижения уровня параллелизма. Граф задания параметризуется априорными оценками длительности 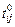 выполнения задачи
выполнения задачи 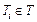 ,
, 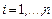 , на ресурсе типа
, на ресурсе типа 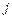 , относительных объемов
, относительных объемов 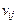 вычислений на процессоре
вычислений на процессоре 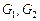 на четырех типах процессоров приведены в табл. 2.1. Длительность всех обменов данными для графа
на четырех типах процессоров приведены в табл. 2.1. Длительность всех обменов данными для графа 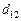 и
и 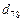 требуют двух, а обмен
требуют двух, а обмен 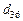 – четырех единиц времени. Полагается, что при укрупнении задач обработки значения соответствующих параметров составляющих подзадач такие суммируются.
– четырех единиц времени. Полагается, что при укрупнении задач обработки значения соответствующих параметров составляющих подзадач такие суммируются.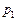
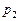
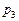
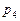
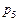
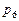
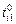
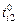
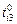
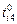
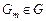 будем именовать моделью задания.
будем именовать моделью задания.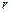 ресурсов между задачами из
ресурсов между задачами из 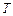 для соответствующей модели задания на отрезке времени
для соответствующей модели задания на отрезке времени 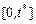
 зададим следующим образом:
зададим следующим образом: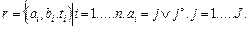
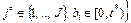 ,
,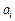 – параметр, определяющий назначение задачи
– параметр, определяющий назначение задачи 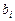 и
и 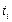 – соответственно момент начала и длительность решения задачи
– соответственно момент начала и длительность решения задачи 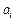 .
. , если задача
, если задача 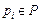 назначается на так называемый базовый ресурс, уровень
назначается на так называемый базовый ресурс, уровень 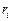 (например, число процессоров) которого ограничен и зависит от возможностей распараллеливания системы задач, стоимости использования ресурса
(например, число процессоров) которого ограничен и зависит от возможностей распараллеливания системы задач, стоимости использования ресурса 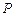 , конкурирующими за один и тот же ресурс типа
, конкурирующими за один и тот же ресурс типа 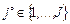 , по своим характеристикам не уступающий базовому, и при этом
, по своим характеристикам не уступающий базовому, и при этом 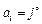 . Это может быть, например, дополнительный процессорный узел того же типа
. Это может быть, например, дополнительный процессорный узел того же типа 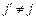 такой, что
такой, что 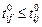 , где
, где 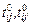 – априорные оценки длительности выполнения задачи
– априорные оценки длительности выполнения задачи 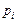 на процессорных узлах соответствующих типов.
на процессорных узлах соответствующих типов.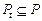 – множество задач, выполняемых в момент времени
– множество задач, выполняемых в момент времени 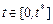 ,
, 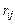 – потребность задачи
– потребность задачи 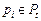 в ресурсе типа
в ресурсе типа 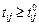 . Например,
. Например, 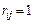 , если
, если 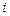 -я задача назначается на процессор
-я задача назначается на процессор 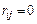 – в противном случае. Тогда необходимое условие разрешение конфликта параллельных задач имеет следующий вид:
– в противном случае. Тогда необходимое условие разрешение конфликта параллельных задач имеет следующий вид: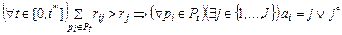 . (2.1.2)
. (2.1.2)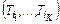 информационно или логических связанных задач,
информационно или логических связанных задач, 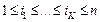 , составляющих задание:
, составляющих задание: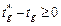 ,
, 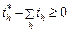 ,
, 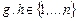 , (2.1.3)
, (2.1.3)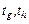 – время решения задач
– время решения задач 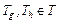 , а
, а 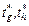 – контрольные сроки завершения выполнения задачи
– контрольные сроки завершения выполнения задачи 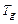 и работы, включающей задачу
и работы, включающей задачу 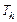 .
.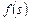 эффективности использования вычислительных ресурсов представим вектором
эффективности использования вычислительных ресурсов представим вектором 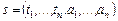 . Пусть
. Пусть 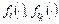 – функции для оценки эффективности выполнения
– функции для оценки эффективности выполнения 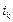 -й задач на ресурсах, типы которых определяются назначениями
-й задач на ресурсах, типы которых определяются назначениями 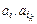 ,
, 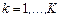 . Критерий
. Критерий 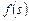 представим следующим образом:
представим следующим образом: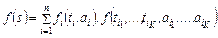 =
= 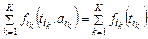 . (2.1.4)
. (2.1.4)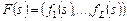 , где каждый из критериев
, где каждый из критериев 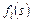 ,
, 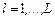 , можно записать в виде (2.1.4).
, можно записать в виде (2.1.4).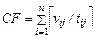 ,
,  – время, отведенное для выполнения задачи
– время, отведенное для выполнения задачи 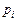 на процессоре типа
на процессоре типа 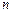 – число задач обработки;
– число задач обработки; 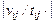
 – частная функция стоимости выполнения
– частная функция стоимости выполнения  означает ближайшее не меньшее целое число.
означает ближайшее не меньшее целое число.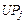 процессоров
процессоров 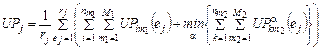 , (2.1.6)
, (2.1.6)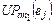 ,
, 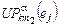 – загрузка
– загрузка 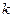 -й задачей в работах
-й задачей в работах 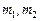 экземпляра
экземпляра 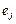 процессоров типа
процессоров типа 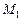 – число работ, выполняемых независимо от условных ветвлений процессов вычислений;
– число работ, выполняемых независимо от условных ветвлений процессов вычислений;  – число
– число 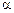 -компонентных наборов альтернативных работ;
-компонентных наборов альтернативных работ; 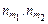 – число задач в работах
– число задач в работах 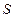 – множество планов, каждый из которых
– множество планов, каждый из которых 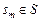 соответствует допустимому распределению ресурсов (2.1.1) и своей модели
соответствует допустимому распределению ресурсов (2.1.1) и своей модели 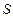 будем использовать понятие оптимальности по бинарному отношению
будем использовать понятие оптимальности по бинарному отношению 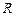 , формируемому векторным критерием
, формируемому векторным критерием 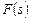 . Например,
. Например, 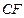 и
и  , согласно (2.1.5) и (2.1.6). Пару
, согласно (2.1.5) и (2.1.6). Пару 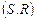 будем называть моделью выбора, а множество
будем называть моделью выбора, а множество 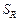 , оптимальных по отношению
, оптимальных по отношению 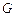 моделей, заключается в отыскании
моделей, заключается в отыскании 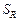 допустимого в соответствии с (2.1.2), (2.1.3) распределения ресурсов (2.1.1), где
допустимого в соответствии с (2.1.2), (2.1.3) распределения ресурсов (2.1.1), где 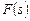 критериев вида (2.1.4). Получаемая стратегия
критериев вида (2.1.4). Получаемая стратегия 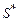 должна обеспечивать приемлемую аппроксимацию: совпадение
должна обеспечивать приемлемую аппроксимацию: совпадение 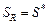 ; включение
; включение 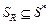 ; совпадение с точностью до эквивалентности
; совпадение с точностью до эквивалентности 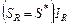 , где
, где 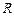 – квазипорядок, а
– квазипорядок, а 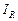 – отношение эквивалентности на
– отношение эквивалентности на 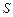 .
.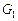 (см. рис. 2.1) первой критической по длительности работе соответствует путь
(см. рис. 2.1) первой критической по длительности работе соответствует путь 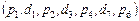 . Его априорная максиминная длительность равна 12 единицам времени (см. табл. 2.1). После назначения задач этой последовательности ресурсы должны распределяться для следующей работы
. Его априорная максиминная длительность равна 12 единицам времени (см. табл. 2.1). После назначения задач этой последовательности ресурсы должны распределяться для следующей работы 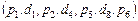 , поскольку не назначены задачи
, поскольку не назначены задачи 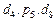 и априорная длительность работы составляет 11 единиц. Распределение ресурсов для последовательности
и априорная длительность работы составляет 11 единиц. Распределение ресурсов для последовательности 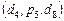 должно учитывать результаты назначения задач первой критической работы.
должно учитывать результаты назначения задач первой критической работы.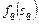 – функция для оценки эффективности выполнения
– функция для оценки эффективности выполнения 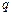 -й работы по критерию
-й работы по критерию 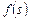 ,
, 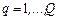 ;
; 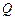 – число работ в задании;
– число работ в задании; 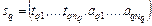 –план;
–план; 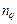 – число задач;
– число задач; 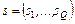 ;
;  – соответственно длительность выполнения и назначение
– соответственно длительность выполнения и назначение 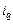 -й задачи,
-й задачи, 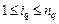 . С учетом свойства аддитивной сепарабельности (2.1.4) критерий
. С учетом свойства аддитивной сепарабельности (2.1.4) критерий 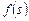 можно представить в виде:
можно представить в виде: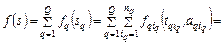
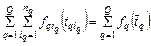 , (2.2.1)
, (2.2.1)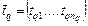 .
.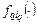 в (2.2.1) при заданном значении запаса
в (2.2.1) при заданном значении запаса 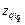 по времени выполнения к моменту запуска
по времени выполнения к моменту запуска 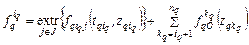 , (2.2.2)
, (2.2.2)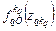 – условный оптимум функции
– условный оптимум функции 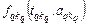 при запасе
при запасе 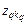 по времени к моменту запуска
по времени к моменту запуска 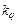 -й задачи при наилучшей комбинации типов ресурсов.
-й задачи при наилучшей комбинации типов ресурсов.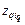 по времени определяются из следующих функциональных уравнений:
по времени определяются из следующих функциональных уравнений: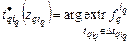 , (2.2.3)
, (2.2.3) . (2.2.4)
. (2.2.4)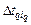 – диапазон изменения длительности
– диапазон изменения длительности 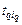 , зависящий от запаса
, зависящий от запаса 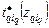 в (2.2.4) получается из (2.2.3)
в (2.2.4) получается из (2.2.3)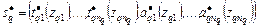 . (2.2.5)
. (2.2.5)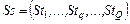 ,
, 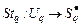 , (2.2.6)
, (2.2.6)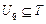 – подмножество задач, образующих
– подмножество задач, образующих 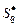 – множество условно оптимальных планов (2.2.5), получаемых на шаге
– множество условно оптимальных планов (2.2.5), получаемых на шаге 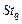 .
.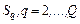 , производится с учетом результатов синтеза множества
, производится с учетом результатов синтеза множества 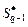 планов, что объясняется необходимостью учета информационно-логических связей в задании и разрешения конфликтов между задачами, конкурирующими за использование разделяемого ресурса.
планов, что объясняется необходимостью учета информационно-логических связей в задании и разрешения конфликтов между задачами, конкурирующими за использование разделяемого ресурса.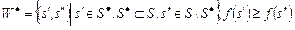 , (2.2.7)
, (2.2.7)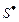 – подмножество планов, являющееся одновременно внутренне и внешне устойчивым в модели выбора
– подмножество планов, являющееся одновременно внутренне и внешне устойчивым в модели выбора 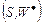 .
. , является условно оптимальным.
, является условно оптимальным.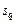 плана
плана 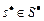 является условно оптимальной.
является условно оптимальной. имеем:
имеем: 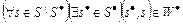 ,
, 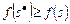 . При этом
. При этом 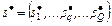 , где
, где 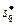 определяется согласно (2.2.5).
определяется согласно (2.2.5).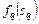 в (2.2.1) обладает свойством (2.1.4) и представляет собой монотонно-рекурсивный функционал, определенный на множестве
в (2.2.1) обладает свойством (2.1.4) и представляет собой монотонно-рекурсивный функционал, определенный на множестве 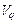 последовательностей
последовательностей 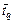 :
: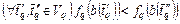 ,
, 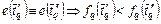 , (2.2.8)
, (2.2.8)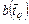 – начало
– начало 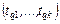 , а
, а 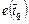 – сопряженное с ним окончание
– сопряженное с ним окончание 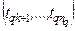 последовательности
последовательности 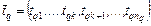 .
.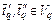 длительностей выполнения задач вида:
длительностей выполнения задач вида: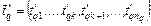 ,
,  .
.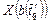 ,
, 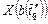 множества всех конечных отрезков допустимых последовательностей из множеств
множества всех конечных отрезков допустимых последовательностей из множеств 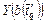 ,
, 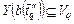 соответственно, причем отрезки из
соответственно, причем отрезки из 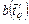 ,
, 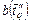 . Множества
. Множества 


