
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Схема выбора эффективной комбинации слотов
Для отыскания Пусть Тогда для (3.3.1), (3.3.2) справедливо
Для схемы (3.3.3), (3.3.4)
Условно оптимальный набор слотов для выполнения Условно оптимальная комбинация слотов
где значения Так, в множество условно оптимальных (при заданном При применении схем (3.3.1), (3.3.2) и (3.3.3), (3.3.4) для каждого из критериев эффективности Обозначим через
Предположим, что
Внешняя устойчивость Далее, в силу внутренней устойчивости
В общем случае
Из-за невозможности выполнения (3.4.10) и справедливости (3.4.11), (3.4.12) следует, что
Таким образом, применение схем (3.3.1), (3.3.2) и (3.3.3), (3.3.4) позволяет сформировать частные стратегии В частности, если
3.4.3. Формирование Положим, необходимо сформировать В табл. 3.4 приведены стратегии, условно оптимальные по критериям стоимости Некоторые из планов, полученных при формировании стратегий с применением различных критериев и схем прогонки, совпадают. В табл. 3.4 это, например, планы 4, 7; 5, 8; 6, 9; 1, 10; 2, 12; 3, 13; 11, 15; 14, 17 и т.д. Оставим лишь первый план из пары совпадающих и сведем их в табл. 3.5.
Таблица 3.4
В ней представлены относительные (нормированные) в соответствии с (3.4.6) значения критериев В пространстве критериев
Таблица 3.5
Конкретная комбинация слотов должна выбираться из стратегии и оформляться соответствующими ресурсными запросами, поступающими в локальные системы пакетной обработки. При этом эффективность той или иной комбинации слотов можно оценить с помощью скалярной функции полезности (3.4.5). Положим, веса нормированных в соответствии с (3.4.6) критериев
Рис. 3.2. Пример стратегии планирования в пространстве двух критериев Выводы В данном разделе рассмотрено решение задач планирования пакетов независимых заданий в распределенных средах с неотчуждаемыми ресурсами на основе методов динамического программирования и циклической схемы. Стратегия планирования строится с применением вектора критериев, формализующих экономическую политику предоставления и потребления ресурсов в виртуальной организации, объединяющей пользователей, собственников и администраторов. Однако этой схеме присущи следующие ограничения. Отсутствует возможность влиять на ход выполнения отдельного пользовательского задания: поиск отдельных альтернатив осуществляется по принципу «первая подходящая», а выбор их оптимальной комбинации отражает интересы всей виртуальной организации. Таким образом, не учитываются предпочтения отдельных пользователей, что не позволяет говорить о справедливом разделении ресурсов. Преодолеть эти ограничения позволяет теоретико-игровой подход к планированию, основы которого излагаются в следующем разделе. 4. МНОГОАГЕНТНОЕ ВЗАИМОДЕЙСТВИЕ и элементы теории игр 4.1. Введение и основные понятия теории игр Введение
При планировании распределенных вычислений с использованием экономических принципов необходимо учитывать интересы и особенности поведения многочисленных участников вычислений: пользователей, запускающих задания, владельцев ресурсов и администраторов виртуальной организации. Как правило, интересы участников вступают в конфликт, так как каждый из них, прежде всего, заинтересован в максимизации личной выгоды. Именно поэтому при проектировании механизма планирования необходимо понимать, как будут вести себя основные участники: какие цели они преследуют, какие имеют способы их достижения, каким образом происходит ценообразование и т.п. Кроме того, одним из образующих качеств виртуальной организации, кроме эффективности планирования, является наличие прозрачных и справедливых правил разделения и использования доступных ресурсов и полученной прибыли.
Для того чтобы приблизиться к пониманию и решению этих проблем мы предлагаем использовать теоретико-игровой подход и далее представим некоторые элементы теории игр, наиболее существенные для анализа и решения поставленных задач. Так, в разделе 4.2 рассматривается проблема выбора стратегий поведения рациональными соперниками, раздел 4.3 содержит и примера механизма, обладающего необходимыми и предсказуемыми экономическими свойствами, а в разделе 4.4 на примере сетевых моделей продемонстрирован итеративный алгоритм распределения сетевых ресурсов.
4.1.2. Основные определения теории игр Теория игр имеет уже довольно богатую историю. Первый научный труд Теория игр и экономическое поведение (Theory of games and Economic Behavior), посвященный этой дисциплине, был издан в 1944 году Джоном фон Нейманом и Оскаром Моргенштерном. Однако, как и во многих других областях науки, отдельными проблемами, ныне относящимися к теории игр, занимались задолго до издания данной книги. Так, многие задачи теории игр были поставлены и решены такими известными учеными, как А.Курно и Ж. Бертран (работы 19го века). Некоторые из этих работ имеют ярко выраженное отношение к экономике, другие направлены на изучение взаимодействия игроков в различных ситуациях, например, в теории шахматной игры. Методы и модели теории игр нашли применение не только в экономике, но и в социологии, биологии, политологии, технике, кибернетике и т.д. В рамках теории игр понятие игра подразумевает соревнование, конкуренцию нескольких участников за победу, за наилучший расклад. Под игрой понимается процесс, в котором участвуют две и более сторон, ведущих борьбу за реализацию своих интересов. Каждая из сторон имеет свою цель и использует некоторую стратегию, которая может вести к выигрышу или проигрышу — в зависимости от поведения других игроков. Теория игр помогает выбрать лучшие стратегии с учётом представлений о других участниках, их ресурсах и их возможных поступках.
Можно выделить и другие определения. Теория игр - это математическая теория принятия оптимальных решений в условиях конфликтов (Н.Н. Воробьев). Теория игр - это теория рационального поведения людей с несовпадающими интересами (Роберт Ауманн). Эти определения дают представление о том, почему теория игр используется даже в таких областях, как биология. Все живые организмы действуют, преследуя свои цели, при этом постоянно контактируют с другими живыми организмами. Таким образом, каждое живое существо должно принимать во внимание интересы и возможные поступки других существ: с совпадающими или несовпадающими полностью, или частично, интересами. Исходя из этого, выделяют два направления в теории: некооперативные и кооперативные (коалиционные) игры. Теория кооперативных игр занимается вопросами выбора партнеров, образования коалиций и справедливого распределения выигрышей между их участниками. Образование коалиций происходит в первую очередь для достижения некоторого общего блага. Справедливость является одним из важнейших факторов, который побуждает игроков образовывать коалиции и стремиться к сотрудничеству. С другой стороны, не всегда возможно дать точное определения справедливости, так как в общем случае для каждого участника оно может отличаться. В теории некооперативных игр рассматриваются задачи выбора оптимальных или равновесных решений для отдельных игроков, а не групп игроков. В данном разделе большее внимание будет уделено теории некооперативных игр. По отношению ко времени игры подразделяются на статические и динамические. В статических играх время принятия игроками решения не имеет значения. Игроки осуществляют ходы одновременно и сразу могут наблюдать результат. Соответственно, каждый игрок при выборе действия в следующем раунде, основывается на действиях соперников в предыдущих раундах. Пример: камень, ножницы, бумага. В динамических играх действия игроков (или очередность ходов) упорядочены во времени. Каждый сделанный ход влияет на будущий ход противника. Пример: шахматы, го, крестики-нолики.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 66; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.76.0 (0.027 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
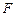 -оптимальной стратегии выполнения системы заданий необходимо формирование стратегий, которые являются условно оптимальными по частным критериям и удовлетворяют (3.4.2)-(3.4.4).
-оптимальной стратегии выполнения системы заданий необходимо формирование стратегий, которые являются условно оптимальными по частным критериям и удовлетворяют (3.4.2)-(3.4.4).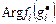 ,
, 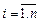 , представляет собой множество значений функции затрат
, представляет собой множество значений функции затрат  , при которых достигается экстремум
, при которых достигается экстремум 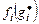 для заданного
для заданного  в схемах обратной (3.3.1), (3.3.2) и прямой (3.3.3), (3.3.4) прогонки.
в схемах обратной (3.3.1), (3.3.2) и прямой (3.3.3), (3.3.4) прогонки.
 ,
, 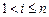 ,
, ,
, 

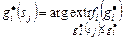 . (3.4.7)
. (3.4.7)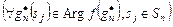
 ,
, ,
, 
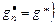
 -го задания будем обозначать через
-го задания будем обозначать через  .
.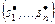 определяется из уравнения
определяется из уравнения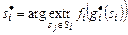 ,
,  , (3.4.9)
, (3.4.9) получаются из (3.4.7), (3.4.8).
получаются из (3.4.7), (3.4.8). ) входит комбинация слотов (1, 2, 3), полученная при решении задачи в подразделе 3.3.3, когда
) входит комбинация слотов (1, 2, 3), полученная при решении задачи в подразделе 3.3.3, когда 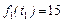 . Все три комбинации слотов, упомянутые в подразделе 3.3.3, условно оптимальны по критерию
. Все три комбинации слотов, упомянутые в подразделе 3.3.3, условно оптимальны по критерию  в соответствии с (3.4.9), поскольку они образуют множество альтернатив, являющееся внутренне и внешне устойчивым в соответствующей модели выбора, где бинарное отношение вида (3.4.2) порождается критерием
в соответствии с (3.4.9), поскольку они образуют множество альтернатив, являющееся внутренне и внешне устойчивым в соответствующей модели выбора, где бинарное отношение вида (3.4.2) порождается критерием  . Условно оптимальными являются комбинации (1, 2, 4) и (2, 2, 4), полученные при решении соответствующей задачи в подразделе 3.4. Они дают суммарное время выполнения пакета заданий, соответственно равное 9 и 7 единицам времени, а затраты составляют 13 и 16 единиц.
. Условно оптимальными являются комбинации (1, 2, 4) и (2, 2, 4), полученные при решении соответствующей задачи в подразделе 3.4. Они дают суммарное время выполнения пакета заданий, соответственно равное 9 и 7 единицам времени, а затраты составляют 13 и 16 единиц.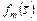 верны соотношения (3.4.2)-(3.4.4). Действительно, условно оптимальные комбинации слотов согласно (3.4.9) образуют внутренне устойчивое множество комбинаций
верны соотношения (3.4.2)-(3.4.4). Действительно, условно оптимальные комбинации слотов согласно (3.4.9) образуют внутренне устойчивое множество комбинаций 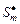 в модели выбора
в модели выбора  . Внешняя устойчивость
. Внешняя устойчивость  следует из того, что
следует из того, что 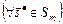

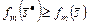 . Наборы вида (3.4.9) позволяют построить условно оптимальные стратегии и в конечном итоге найти
. Наборы вида (3.4.9) позволяют построить условно оптимальные стратегии и в конечном итоге найти 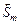 и
и 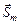 стратегии, условно оптимальные по критерию
стратегии, условно оптимальные по критерию 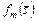 , полученные соответственно по схемам обратной (3.3.1), (3.3.2) и прямой (3.3.3), (3.3.4) прогонки. Заметим, что в общем случае
, полученные соответственно по схемам обратной (3.3.1), (3.3.2) и прямой (3.3.3), (3.3.4) прогонки. Заметим, что в общем случае 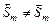 . Пусть
. Пусть 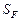 является
является  , где бинарное отношение
, где бинарное отношение 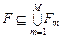 , где
, где 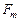 определяется согласно (3.4.2). Тогда
определяется согласно (3.4.2). Тогда  является стратегией, условно оптимальной по критерию
является стратегией, условно оптимальной по критерию 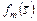 , поскольку имеет место (3.4.3), (3.4.4).
, поскольку имеет место (3.4.3), (3.4.4).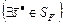
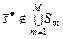 . (3.4.10)
. (3.4.10)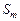 в модели выбора
в модели выбора  исключает существование такой комбинации слотов
исключает существование такой комбинации слотов  и делает невозможным (3.4.10).
и делает невозможным (3.4.10).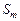 в
в 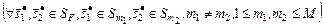
 ,
,  . (3.4.11)
. (3.4.11)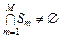 . Пусть
. Пусть 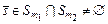 ,
,  . Тогда
. Тогда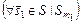
 ,
, 
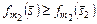 . (3.4.12)
. (3.4.12)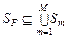 . (3.4.13)
. (3.4.13)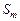 , условно оптимальные по каждому из критериев эффективности
, условно оптимальные по каждому из критериев эффективности 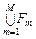 , поскольку справедливо (3.4.1) и при этом
, поскольку справедливо (3.4.1) и при этом 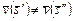 .
. строится на объединении стратегий, сформированных с применением частных критериев (подраздел 3.4.2). Пусть
строится на объединении стратегий, сформированных с применением частных критериев (подраздел 3.4.2). Пусть 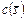 и времени
и времени 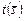 выполнения пакета заданий. Они включают 13 комбинаций слотов (планов), которые сформированы в ходе решения модельных задач, рассмотренных в подразделах 3.3.3 –3.3.6 методом обратной прогонки по (3.3.1), (3.3.2). Варианты 14 - 25 получены методом прямой прогонки в соответствии с (3.3.3), (3.3.4). Планы 1 – 3; 7 – 9; 14 – 16; 20 – 22 являются условно оптимальными по
выполнения пакета заданий. Они включают 13 комбинаций слотов (планов), которые сформированы в ходе решения модельных задач, рассмотренных в подразделах 3.3.3 –3.3.6 методом обратной прогонки по (3.3.1), (3.3.2). Варианты 14 - 25 получены методом прямой прогонки в соответствии с (3.3.3), (3.3.4). Планы 1 – 3; 7 – 9; 14 – 16; 20 – 22 являются условно оптимальными по 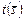 .
.
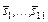 .
. и
и 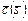 , имеющих одинаковую важность, альтернативы
, имеющих одинаковую важность, альтернативы 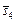 и
и 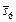 доминируют над всеми остальными и образуют подмножество Парето (рис. 3.2).
доминируют над всеми остальными и образуют подмножество Парето (рис. 3.2).

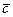

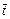

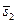
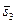

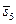
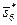



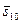
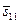
 ,
,  равны. Тогда наилучшим компромиссным решением является план
равны. Тогда наилучшим компромиссным решением является план  с минимальным значением 0,15 функции полезности
с минимальным значением 0,15 функции полезности 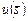 . Именно этот план и должен быть оформлен ресурсными запросами к локальным вычислительным узлам в виде резервирования соответствующих слотов.
. Именно этот план и должен быть оформлен ресурсными запросами к локальным вычислительным узлам в виде резервирования соответствующих слотов.



