Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перетворення звичайного дробу в систематичний і визначення довжини періоду систематичного дробу.⇐ ПредыдущаяСтр 13 из 13
Розглянемо питання про перетворення звичайного дробу в десятковий. Як відомо з арифметики звичайні дроби перетворюються або в скінченні, або не в скінченні періодичні десяткові дроби. При цьому звичайний дріб Легко зрозуміти, що нескоротний дріб виду Справді, припускаючи супротивне,маємо
Звідки Теорема 1. Якщо канонічний розклад знаменника Доведення. Для спрощення дріб
Цю схему в свою чергу можна подати у вигляді системи рівностей:
..............................
........................................... Де
а будь-які числа Проаналізуємо властивості чисел
Оскільки числа
Для доведення теореми залишається показати, що перше повторення настане після кроків проміжних обчислень, де – показник, до якого належить 10 за модулем
то при
Остання конгруенція якраз і показує, що, приписавши до Зауваження. З конгруенції Іншими словами, число 999…9, що складається з дев’яток – найменше з можливих чисел такої структури, яке ділиться на Теорема 2. Якщо канонічний розклад знаменника Доведення. Дріб
помножимо на
і далі
За теоремою 1, дріб
Приклади. 1. Знайти число цифр періоду десяткового періодичного дробу, в який перетворюється дріб Ділимо на 39 послідовно числа 9, 99, 999, 9999, 99999. Нарешті з’ясовується, що тільки число 999999 націло ділиться на 39. Кількість дев’яток у цьому числі визначає довжину періоду: 2. Знайти число цифр, яке міститься до періоду, і довжину періоду періодичного дробу, в який перетворюється дріб Знаменник цього дробу в канонічному розкладі має вигляд
.
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 142; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.113.197 (0.017 с.) |
||||||||||||||||||||||||||||||||||||||||||||||
 перетворюється в скінченний десятковий дріб тоді і тільки тоді, коли канонічний розклад знаменника має вигляд
перетворюється в скінченний десятковий дріб тоді і тільки тоді, коли канонічний розклад знаменника має вигляд 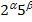 . тобто не містить ніяких простих множників, крім 2 і 5. Для спрощення вважатимемо
. тобто не містить ніяких простих множників, крім 2 і 5. Для спрощення вважатимемо  нескоротним правильним дробом.(Якщо він неправильний, то можна спочатку виділити цілу частину). Звичайні нескоротні і правильні дроби виду
нескоротним правильним дробом.(Якщо він неправильний, то можна спочатку виділити цілу частину). Звичайні нескоротні і правильні дроби виду 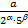 перетворюються в скінченні десяткові дроби з числом десяткових знаків, яке дорівнює найбільшому з чисел a або b. Справді, якщо a=b то
перетворюються в скінченні десяткові дроби з числом десяткових знаків, яке дорівнює найбільшому з чисел a або b. Справді, якщо a=b то 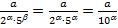 скінченний десятковий дріб. Якщо
скінченний десятковий дріб. Якщо 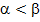 , то
, то 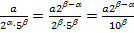 скінченний десятковий дріб. Якщо
скінченний десятковий дріб. Якщо 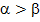 , то
, то 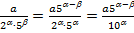 скінченний десятковий дріб.
скінченний десятковий дріб.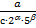 , де
, де 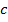 відмінне від 2 і 5, в скінченний десятковий дріб не перетворюється.
відмінне від 2 і 5, в скінченний десятковий дріб не перетворюється.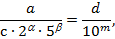
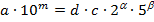 , де
, де 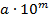 , що неможливо, бо
, що неможливо, бо 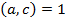 . Ця суперечність доводить справедливість твердження.
. Ця суперечність доводить справедливість твердження.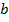 нескороченого дробу
нескороченого дробу 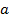 на число
на число 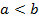 можна схематично зобразити так:
можна схематично зобразити так: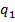
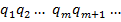
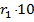
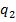
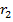
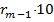 b
b 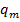
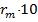 b
b 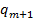
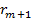 ………
………
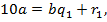
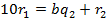
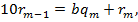
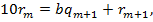
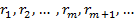 — остачі, а
— остачі, а 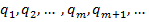 — частки проміжних обчислень. Будь-яка остача
— частки проміжних обчислень. Будь-яка остача 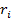 , очевидно, задовольняє нерівність
, очевидно, задовольняє нерівність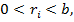
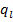 задовольняють нерівність
задовольняють нерівність 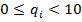 , тобто є цифрами, з яких складається частка 0,
, тобто є цифрами, з яких складається частка 0, 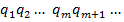 в схемі (4).
в схемі (4).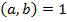 і
і 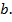 Справді
Справді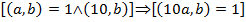
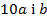 взаємно прості, то з першої рівності (5) випливає, що
взаємно прості, то з першої рівності (5) випливає, що 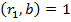 . Справді за умови
. Справді за умови 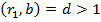 випливало б, що вся права частина, а отже, і ліва частина ділилась би на
випливало б, що вся права частина, а отже, і ліва частина ділилась би на 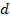 . Тому числа
. Тому числа 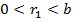 і
і 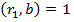 випливає, що остача
випливає, що остача 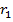 є одним з найменших додатних лишків ЗСЛ за модулем
є одним з найменших додатних лишків ЗСЛ за модулем 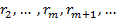 є найменшими додатними лишками ЗСЛ за модулем
є найменшими додатними лишками ЗСЛ за модулем 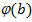 найменших додатних лишків. Тому в системі рівностей (5) настане момент, коли одна з остач дорівнюватиме
найменших додатних лишків. Тому в системі рівностей (5) настане момент, коли одна з остач дорівнюватиме 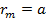 . Тоді
. Тоді 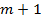 рівність (5) збіжиться з першою рівністю цієї системи. І тому …. Далі, … рівність збіжиться з другою рівністю (5) і тому
рівність (5) збіжиться з першою рівністю цієї системи. І тому …. Далі, … рівність збіжиться з другою рівністю (5) і тому  . Таким чином, остачі
. Таким чином, остачі 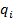 проміжних обчислень повторюватимуться. Тим самим частка в схемі (4) буде чистим періодичним десятковим дробом виду
проміжних обчислень повторюватимуться. Тим самим частка в схемі (4) буде чистим періодичним десятковим дробом виду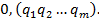
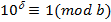
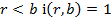 рівносильною їй є і конгруенція
рівносильною їй є і конгруенція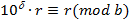
 нулів, що відповідає визначенню послідовних цифр частки, дістанемо при діленні
нулів, що відповідає визначенню послідовних цифр частки, дістанемо при діленні 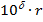 на
на 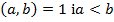 аналогічно дістанемо через ділень остачу, яка дорівнює числу
аналогічно дістанемо через ділень остачу, яка дорівнює числу 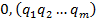 , що й треба було довести.
, що й треба було довести.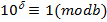 випливає, що
випливає, що 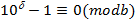 або
або 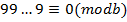 .
.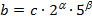 ,де
,де 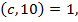 то цей дріб перетворюється у мішаний періодичний дріб; число цифр до періоду дорівнює g, де g – найбільше з чисел a і b; число цифр періоду дорівнює d, де d – показник, якому належить число 10 за модулем
то цей дріб перетворюється у мішаний періодичний дріб; число цифр до періоду дорівнює g, де g – найбільше з чисел a і b; число цифр періоду дорівнює d, де d – показник, якому належить число 10 за модулем  .
.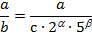
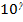 , де
, де 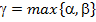 . Матимемо
. Матимемо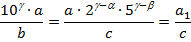
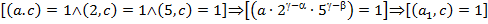
 перетворюється в чистий періодичний дріб з числом цифр у періоді, яке дорівнює , де – показник, до якого належить 10 за модулем
перетворюється в чистий періодичний дріб з числом цифр у періоді, яке дорівнює , де – показник, до якого належить 10 за модулем 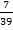 .
.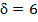 .
.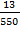 .
.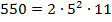 . Тому
. Тому 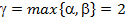 є найбільшим з показників степеня цифр 2 і 5. Це означає, що періодичний десятковий дріб має дві цифри до періоду. Найменше з чисел, складених з дев’яток, яке ділиться на 11, є число 99. Воно складається з двох дев’яток. Це означає, що довжина … періоду періодичного дробу дорівнює 2. І справді, як неважко перевірити, розглядуваний дріб перетворюється в такий періодичний дріб:
є найбільшим з показників степеня цифр 2 і 5. Це означає, що періодичний десятковий дріб має дві цифри до періоду. Найменше з чисел, складених з дев’яток, яке ділиться на 11, є число 99. Воно складається з двох дев’яток. Це означає, що довжина … періоду періодичного дробу дорівнює 2. І справді, як неважко перевірити, розглядуваний дріб перетворюється в такий періодичний дріб: