
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод линейной свертки и Метод ранжирования альтернатив для поддержки принятия решения по выбору средств защитыСодержание книги
Поиск на нашем сайте
1.1 ЦЕЛЬ РАБОТЫ
Осуществить выбор наилучшего варианта средства защиты информации, входящего в государственный реестр сертифицированных средств защиты, с учетом выделенных ресурсов.
ЗАДАЧИ Разработать алгоритм и написать программу для выбора средства защиты по методу линейной сверки критериев и для выбора средства защиты с использованием метода ранжирования альтернатив по свойствам. 1.3. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Многокритериальный рациональный выбор состоит в нахождении тех объектов, которые максимально соответствуют общей цели. Таким образом, решение задачи рационального многокритериального выбора согласно желаниям или индивидуальным предпочтениям лица, принимающего решение, состоит в отыскании номеров объектов, максимизирующих обобщенную меру принадлежности. Пусть N - множество объектов, которое требуется классифицировать с учетом множества n -параметров. Число объектов предполагается конечным и достаточно малым. Частные оценки объектов по каждому отдельно взятому параметру принимают свои значения в легко устанавливаемых диапазонах. Множество объектов может быть упорядочено по каждому параметру. Предполагается также независимость выбора от состояния среды, т. е. предпочтение по одному из параметров не зависит от того, какие значения при этом принимают другие параметры. Задача агрегатирования параметров для получения окончательной оценки рассматривается как задача комбинирования нечетких множеств с помощью теоретико-множественных операций над ними. В качестве таких операций были выбраны две: – первая операция - нахождение суммы значений функций принадлежности среди множества параметров или нахождение суммы мест в матрице ранжирования; – вторая операция - нахождение произведений значений функций принадлежности среди множества параметров или произведение суммы мест в матрице ранжирования. 1.3.1 Метод линейной свертки критериев с весами α i.
Выбирают альтернативу, у которой сумма значений критериев максимальна. Развитие этой идеи сравнения различных критериев ведет к максимизации некоторых функций от критериев f (К С1, К С2,…, К С n). Вид этой функции:
где N – количества критериев, K Cn (n =1,…, N) - множество значений критериев, найденных в соответствии с функциями предпочтения, αn (n=1,..., N) - множество значений весов. При этом Этот вид функции наиболее употребителен и называется линейной сверткой критериев с весами αi, характеризующими степень важности критериев. Сложение критериев друг с другом и другие операции с ними физически редко бывают обоснованными. Введение функций от критериев в большинстве случаев - вынужденная мера, ведущая к необходимости экспертного определения весов отдельных критериев. Для равноважных критериев Лучшей альтернативой будет та, для которой значение функции f будет максимальным.
|
||||
|
Последнее изменение этой страницы: 2020-11-28; просмотров: 191; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.219.11 (0.007 с.) |


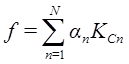 , (1.1)
, (1.1)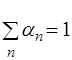 .
.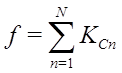 (1.2)
(1.2)


