
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Механическое движение. Поступательное движение: траектория; кинематические параметры – радиус-вектор, перемещение, путь, средняя и мгновенная скоростьСодержание книги
Поиск на нашем сайте
Механическое движение. Поступательное движение: траектория; кинематические параметры – радиус-вектор, перемещение, путь, средняя и мгновенная скорость Мех. движение – это перемещение тел в пространстве с течением времени. Поступательное движение твердого тела – это движение, при котором любая прямая, проведенная в теле, перемещается параллельно самой себе. Понятие материальной точки (МТ). За материальную точку может быть принято любое тело, обладающее массой, размерами которого в условиях данной задачи можно пренебречь. Линия, описываемая материальной точкой в пространстве при ее движении, называется траекторией. Уравнение траектории для плоского движения имеет вид
Движение материальной точки в пространстве определяется законом движения, который для МТ может быть задан в виде трех скалярных уравнений:
либо эквивалентным векторным уравнением:
Быстроту движения материальной точки характеризуют средней скоростью
где s – путь, пройденный за время
которая может быть записана, как любой вектор, в координатной форме:
где проекции скорости
Мгновенное ускорение точки. Разложение полного ускорения на нормальное и тангенциальное. Классификация видов движения Быстроту изменения скорости при неравномерном движении характеризует ускорение: с реднее ускорение
и мгновенное ускорение
С другой стороны, вектор полного ускорения
где проекции вектора ускорения равны соответствующим производным по времени от проекций скорости:
В криволинейном движении осями координат могут быть касательная к траектории движения материальной точки и нормаль к ней. Орты осей в этом случае
где тангенциальное ускорение
нормальное ускорение характеризует быстроту изменения направления скорости и направлено по нормали к центру кривизны траектории:
Здесь Классификация видов движения 1) равномерное прямолинейное дв-е: 2) Равномерное движение по окружности радиуса 3) Равноускоренное движение: 4) Равнозамедленное дв-е: 3. Кинематические уравнения поступательного движения Зная зависимость вектора скорости от времени
Так для равнопеременного поступательного движения МТ (
Тогда закон дв-я МТ:
Динамика поступательного движения. Понятия массы, силы, импульса тела, импульса силы. Взаимодействие тел: Виды сил в механике Динамика изучает причины движения – это взаимодействие тел. Мера взаимодействия – сила Принцип суперпозиции сил (независимости их действия):
Масса тела
Импульс тела – это количество его поступательного движения, равное
Импульс силы: произведение силы на время ее действия:
Виды сил в механике: Сила тяжести
Сила тяготения:
Упругая сила по закону Гука:
Силы трения: трение покоя: трение скольжения: Силы сопротивления при движении тела в среде (воздух, вода и др.) зависят от скорости тела
При больших скоростях тел (например, ракета):
Примеры проявления и использования ЗСМИ Закон сохранения момента импульса (ЗСМИ) можно применять к любой механической системе при условии, что результирующий момент всех внешних сил, приложенных к системе, равен нулю Момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени:
Здесь записана сумма векторов моментов импульса всех частей системы. Момент импульса твердого тела равен произведению его момента инерции на угловую скорость:
Пример применения ЗСМИ: в решении задачи, где человек идет по краю диска, который может вращаться вокруг вертикальной оси; этот закон позволяет найти скорость вращения диска: он вращается в противоположном направлении. Понятие потенциальной энергии. Градиент потенциальной энергии. Примеры вычисления потенциальной энергии Потенциальная энергия – энергия, обусловленная взаимодействием тел и зависящая от положения тел или их частей относительно друг друга. Потенциальной энергией обладают все упруго деформированные тела, например, растянутая или сжатая пружина, а также все тела, которые притягиваются или отталкиваются друг от друга: Земля и другие планеты, взаимодействующие с Солнцем, молекулы, заряженные тела. Потенциальная энергия всегда взаимная, она относится к обоим взаимодействующим телам. Для тела массой m, поднятого над поверхностью Земли на высоту h, потенциальная энергия
Эта формула справедлива только для случая, когда Для упруго деформированной пружины (пластины) и т. п.
где k – коэффициент упругости или жесткость пружины; Вид функции потенциальной энергии находят, вычисляя неопределенный интеграл:
где
где Таким образом, потенциальная и кинетическая энергия тела являются величинами относительными, т. е. их численное значение зависит от выбора системы отсчета. Градиент потенциальной энергии – это вектор, направленный в сторону наибольшего возрастания энергии:
Проекция градиента
Гармонического колебания Уравнение гармонического колебания
позволяет найти скорость частицы, совершающей колебания:
Тогда кинетическая энергия гармонических колебаний
где m – масса колеблющегося объекта; Потенциальная энергия гармонических колебаний
где Полная механическая энергия гармонических колебаний
При гармонических колебаниях выполняется ЗСМЭ, так как эти колебания происходят под действием упругой или квазиупругой силы:
23. Затухающие колебания. Дифференциальное уравнение, закон колебаний. Логарифмический декремент затуханий. Уравнение затухающего колебательного движения:
Здесь Быстроту затухания колебаний характеризуют логарифмическим декрементом затухания
где Циклическая частота затухающих колебаний
где
Механическое движение. Поступательное движение: траектория; кинематические параметры – радиус-вектор, перемещение, путь, средняя и мгновенная скорость Мех. движение – это перемещение тел в пространстве с течением времени. Поступательное движение твердого тела – это движение, при котором любая прямая, проведенная в теле, перемещается параллельно самой себе. Понятие материальной точки (МТ). За материальную точку может быть принято любое тело, обладающее массой, размерами которого в условиях данной задачи можно пренебречь. Линия, описываемая материальной точкой в пространстве при ее движении, называется траекторией. Уравнение траектории для плоского движения имеет вид
Движение материальной точки в пространстве определяется законом движения, который для МТ может быть задан в виде трех скалярных уравнений:
либо эквивалентным векторным уравнением:
Быстроту движения материальной точки характеризуют средней скоростью
где s – путь, пройденный за время
которая может быть записана, как любой вектор, в координатной форме:
где проекции скорости
|
||||
|
Последнее изменение этой страницы: 2020-11-28; просмотров: 407; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.17.251 (0.008 с.) |

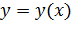 .
.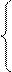
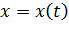 ,
, ,
,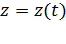 ,
,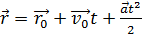 .
.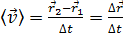 или
или 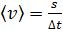 ,
,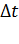 , и мгновенной скоростью
, и мгновенной скоростью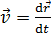 ,
,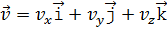 , а модуль
, а модуль 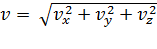 ,
,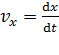 ;
;  ;
; 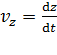 .
.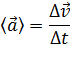
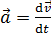 .
.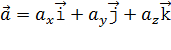 ,
,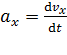 ;
; 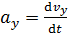 ;
; 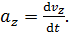
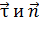 . При этом полное ускорение
. При этом полное ускорение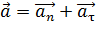 , а его модуль
, а его модуль 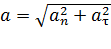 ,
,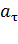 характеризует быстроту изменения модуля скорости и направлено по касательной к траектории:
характеризует быстроту изменения модуля скорости и направлено по касательной к траектории: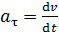 , вектор
, вектор 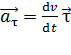 ;
;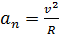 , вектор
, вектор 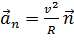 .
. – радиус кривизны траектории.
– радиус кривизны траектории. т.к.
т.к. 
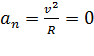 , т.к.
, т.к. 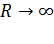 .
.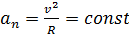 , т.к.
, т.к. 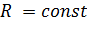 и
и 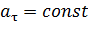 .
.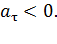
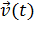 , можно найти закон движения
, можно найти закон движения 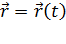 :
: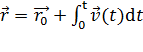
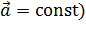 получим:
получим: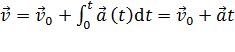 .
.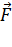 . Единица измерения – 1 Н (ньютон).
. Единица измерения – 1 Н (ньютон). .
. – мера инертности тела и мера его гравитационных свойств (из закона всемирного тяготения):
– мера инертности тела и мера его гравитационных свойств (из закона всемирного тяготения):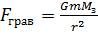 .
.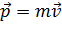 ;
;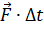 ;
;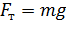 .
. ;
; ;
;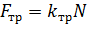 ;
; 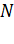 – нормальная реакция опоры.
– нормальная реакция опоры.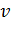 :
: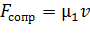 ;
;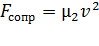 .
.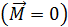 . Формулировка закона:
. Формулировка закона: .
. , – а момент импульса системы тел есть векторная сумма моментов импульса всех тел данной системы:
, – а момент импульса системы тел есть векторная сумма моментов импульса всех тел данной системы: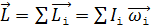 .
. определяется по формуле
определяется по формуле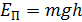 .
. , где
, где  – радиус Земли, и если за нулевой уровень
– радиус Земли, и если за нулевой уровень 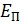 принимают энергию тела на поверхности Земли.
принимают энергию тела на поверхности Земли.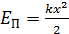 ,
, – величина деформации: удлинение или сжатие тела.
– величина деформации: удлинение или сжатие тела.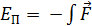
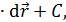
 – постоянная интегрирования, зависящая от выбора нулевого уровня
– постоянная интегрирования, зависящая от выбора нулевого уровня  , получаем
, получаем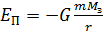 ,
, 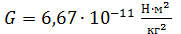 – гравитационная постоянная; m и
– гравитационная постоянная; m и 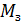 – массы тела и Земли; r – расстояние от центра Земли до центра масс тела. Формула дает значение
– массы тела и Земли; r – расстояние от центра Земли до центра масс тела. Формула дает значение  .
.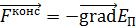 .
.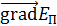 на направление силы равна производной от функции
на направление силы равна производной от функции  :
: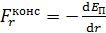 ;
; 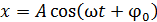 ,
,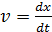 .
.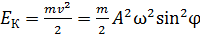 ,
,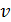 – его скорость.
– его скорость. ,
, – жесткость, или коэффициент упругости пружины.
– жесткость, или коэффициент упругости пружины.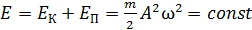 .
.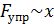 .
.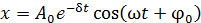 .
.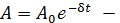 амплитуда затухающих колебаний;
амплитуда затухающих колебаний; 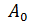 – начальная амплитуда (в момент времени
– начальная амплитуда (в момент времени  ); d – коэффициент затухания, его величина
); d – коэффициент затухания, его величина 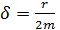 , где r – коэффициент сопротивления среды; m – масса колеблющейся точки.
, где r – коэффициент сопротивления среды; m – масса колеблющейся точки.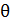 :
: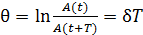 ,
,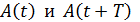 – амплитуды двух последовательных колебаний, отделенных друг от друга периодом колебаний T.
– амплитуды двух последовательных колебаний, отделенных друг от друга периодом колебаний T.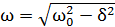 ,
,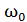 – циклическая частота свободных (собственных) незатухающих колебаний той же колебательной системы.
– циклическая частота свободных (собственных) незатухающих колебаний той же колебательной системы.


