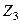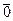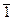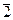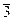Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ГЛАВА 1. Алгебраические структуры.Содержание книги Поиск на нашем сайте
Приходовский М.А. Алгебра (курс лекций) ИПМКН ТГУ, группы 932024, 932025 Осень -2020 ЛЕКЦИЯ 1. 9.11.2020 ГЛАВА 1. Алгебраические структуры. Бинарные алгебраические операции. Взаимосвязь между матанализом и алгеброй. В матанализе изучаются, в частности, функции одного и двух аргументов. Пример 1. Пример 2. Если множество, на котором задано отображение - не числовая прямая, а какое-то дискретное множество, то применяются алгебраические понятия - унарные и бинарные алгебраические операции (по числу аргументов). Существуют и n-арные операции, например, общий перпендикуляр к трём векторам в 4-мерном пространстве (тогда n=3).
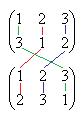
Простейшие примеры. Отображение множества из 3 первых натуральных чисел в само себя. Если в верхней строке записать числа по порядку, а в нижней строке - образ каждого из них, то получится, к примеру, такая запись:
Подстановка. Впрочем, верхняя строка информации не несёт, можно писать только 2-ю строку, это называется перестановкой. Пример: (3 1 2). Перестановок 2 порядка всего две: (1 2) и (2 1). Перестановки 3 порядка: (1 2 3), (1 3 2) (2 1 3), (2 3 1) (3 1 2), (3 2 1). Их всего 6. Чтобы перечислить их все, можно на 1 месте поставить число, а на двух других остаётся по 2 варианта расположить оставшиеся 2 числа. Лемма. Существует n! перестановок порядка n. Доказательство. Для n = 2 это очевидно, перестановки только (12) и (21). Дальше, доказательство по индукции. Пусть теперь для (n-1) этот факт доказан. Рассмотрим для n. На первом месте может стоять любое из n чисел, и при каждой из этих ситуаций, остаётся (n-1) число, которые должны занять (n-1) место, а это возможно (n-1)! способами. Итак, получается
В частности, при n = 3 получается 6 перестановок: (123) (132) (213) (231) (312) (321) На первом месте одно из 3 чисел, и при этом оставшиеся 2 числа можно расставить на 2 места двумя способами. Получается 6 способов. Заметим, что 3! = 6.
Назовём инверсией такую ситуацию, когда большее число в перестановке расположено раньше, чем меньшее. В перестановке (12) инверсий нет, количество инверсий 0, то есть чётно. В перестановке (21) одна инверсия (то есть, их количество нечётно).
Группоид Определение 1. На множестве
Примечание. Результат операции также принадлежит М, другими словами, множество замкнуто относительно этой операции. Это означает, что задано отображение (задана функция) Граница между матанализом и алгеброй очень тонкая. И та, и другая область математики изучает отображения. В матанализе они называются функциями, здесь - алгебраическими операциями. Операция, например, может быть сложением или умножением, но не обязательно, на самом деле существует более обширный класс операций, а сложение и умножение - лишь частные случаи.
Определение 2. Если на
Примеры. 1. Множество целых чисел с операцией сложения. 2. Множество целых чисел с операцией умножения. 3. 4. Множество натуральных чисел с операцией вычитания. Не является группоидом, так как эта операция может привести к тому, что результат не принадлежит данному множеству, например, если
Свойства операций. 1. Коммутативность. Если для любых Примеры. 1. 5. 2. Ассоциативность. Если Примеры. 1. 5.
Нейтральный элемент. Пусть дан группоид
Пример 1. Пример 2. Нейтральный элемент существует не всегда. Пример 3. Векторное умножение в пространстве. Если каждой паре векторов ставится в соответствие их общий перпендикуляр, то результат действия операции перпендикулярен каждому из векторов, и невозможна ситуация
Пример 4.
Лемма. Если существует нейтральный элемент, то он единственный. Доказательство. Допустим, что существует 2 нейтральных элемента,
Симметричный (обратный) элемент Определение. Пусть группоид Примеры. 1. При сложении, в 2. При умножении, в 3. Лемма. Пусть Доказательство. Пусть для
Пример. Подстановки, нейтральный обратный элемент:
Группы Определение. Множество 1) выполняется ассоциативность, т.е.
2) существует нейтральный элемент 3) Примеры.
Если операция коммутативна, то группа называется коммутативной, или абелевой. Определение подгруппы. Непустое подмножество Примеры. Крайние случаи: 1) сама группа есть подгруппа, 2) множество, состоящее только из нейтрального элемента, Пример. Впрочем, подгруппой является любое подмножество вида Пример. Подмножество Примеры.
Пример. Конечная группа, дана таблица умножения элементов:
Похоже на то, что было при изучении подстановок, только не унарная, а бинарная операция. Есть
--- перерыв --- Доказательство. 1. Необходимость - очевидно, по определению, если 2. Достаточность. Если Тогда для всякого Примечание. Этот критерий - фактически эквивалентное свойство, которое могло бы быть принято в качестве определения подгруппы. Теорема 2. Если
Доказательство. Если Но каждая
Пример. Подгруппы Пример. Группа подстановок 1) Ассоциативность есть.
С другой стороны, 2) Нейтральный элемент 3) Обратный элемент. Если Пример. Подгруппа Пример. Подмножество всех нечётных подстановок - не образует подгруппу, потому что: произведение подстановки и обратной к ней (обе нечётные) это тождественная подстановка, а она содержит 0 инверсий, значит - чётная, но тогда она не принадлежит этому подмножеству.
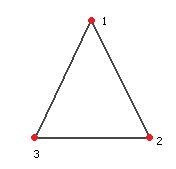
Пример. Группы движений и симметрий правильных n-угольников. Например, для треугольника. Каждый поворот или зеркальное отражение, при котором 3 вершины переходят в какие-то другие, соответствует подстановке.
Но при этом можно заметить, что всякое отражение может быть получено как композиция какого-то одного базового отражения (например, где меняются вершины 1 и 2) и поворота.
Для
ЛЕКЦИЯ 2. 14.11.2020 Кольца Теперь рассмотрим множества не с одной, а с двумя различными операциями. Интуитивно вам уже известны такие примеры: сложение и умножение на множестве чисел, к тому же, для них известен закон дистирибутивности: Определение. Пусть 1) 2) 3) операции сложения и умножения связаны законами дистрибутивности: Тогда Если существует нейтральный элемент по умножению, то кольцо называется кольцом с единицей. Если операция умножения коммутативна, то называется «коммутативное кольцо». Примеры. 1)Числовые кольца. 2) Кольцо функций. Функции, заданные на
По сложению есть противоположный элемент.
3) Множество векторов в 3-мерном пространстве относительно операции векторного умножения. Это пример некоммутативного кольца, и без единицы.
Лемма. 1. При умножении любого элемента на 2. Произведение 1-го элемента на противоположный ко 2-му это то же самое, что произведение противоположного 1-му на 2-й, и равно противоположному к их суммарному произведению, т.е. Доказательство. 1. 2.
Определение. Непустое подмножество Примеры. Все непрерывные на Теорема 1. (критерий подкольца). Непустое множество 1) Доказательство. Необходимость - очевидно. Если подкольцо, то произведение принадлежит, кроме того, Достаточность. Если для любой пары элементов Операция ассоциативна и на подмножестве, поэтому Дистрибутивность также сохраняется на подмножестве. Вывод:
Обратимые элементы. Определение. Пример. В кольце В кольцах В кольце функций (с поточечным умножением) обратимые элементы это те функции, которые ни в одной точке не обращаются в 0.
Делители нуля Определение. Если Пример в кольце функций. В числовых множествах делителей нуля нет. В кольце матриц есть, например,
Теорема 2. Обратимый элемент кольца не может являться делителем нуля. Доказательство. Пусть
но с другой стороны, Значит,
Замечание. Обратное утверждение к теореме 2 неверно, т.е. из того, что он не делитель нуля, не следует, что обратимый. Пример: в кольце
Теорема 3. О мультипликативной группе кольца. Все обратимые элементы кольца Доказательство. Докажем, что если
Кроме того, Обратный к любому элементу также Идеал кольца. Определение. Подкольцо
Пример во множестве функций. Все функции, обращающиеся в 0 в точке
Кольца вычетов. Определение. Два целых числа называются сравнимыми по модулю n, если при делении на n они дают одинаковые остатки, т.е. если их разность делится на n: Обозначается Например, числа 1, 4, 7, 10, 13,... дают при делении на 3 остаток 1. При этом разность любых из них делится на 3. Таким образом, множество
Свойства сравнимости. 1. 2. 3. Из этих 3 свойств следует, что сравнимость является отношением эквивалентности в Свойство 4. Докажем это свойство, оно не очевидно.
Пример. 4 и 7 5 и 8 разность 3 тогда 9 и 15 разность кратна 3 тоже. Свойство 5. Докажем это свойство.
Пример. 4 и 7 5 и 8 разность 3 тогда 20 и 56 разность 36, кратна 3.
Если Классы вычетов попарно не пересекаются: Обозначим Это можно сделать, так как из свойств 4 и 5, ранее доказанных, следует, что произведение не зависит от выбора представителя класса. Итак, на конечном множестве из n элементов заданы 2 операции, сложение и умножение. Множество классов вычетов тоже образует кольцо Другое обозначение класса вычетов: Например,
- - - Перерыв - - - Очевидно, Составим таблицы сложения. Первый пример - для
Обратите внимание, 3 простое число, и при умножении в каждой строке есть все классы. Составим таблицы сложения и умножения для кольца
|

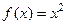 , т.е.
, т.е. 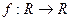
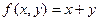 , здесь
, здесь 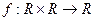
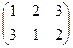
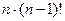 что как раз равно n!, что и требовалось доказать.
что как раз равно n!, что и требовалось доказать.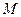 задана бинарная алгебраическая операция, если каждой паре элементов
задана бинарная алгебраическая операция, если каждой паре элементов 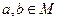 поставлен в соответствие однозначно определённый элемент
поставлен в соответствие однозначно определённый элемент 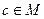 .
.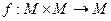 ,
, 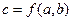 . В матанализе используется функциональные обозначения
. В матанализе используется функциональные обозначения 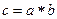 .
. 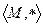 .
. 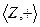 является группоидом, так как результат операции - это снова целое число, то есть операция не выводит за пределы этого множества.
является группоидом, так как результат операции - это снова целое число, то есть операция не выводит за пределы этого множества.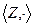 . Аналогично прошлому примеру, является группоидом.
. Аналогично прошлому примеру, является группоидом.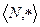 , где
, где 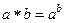 является группоидом. Положительная степень натурального числа есть снова натуральное число.
является группоидом. Положительная степень натурального числа есть снова натуральное число.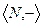 .
. 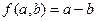 .
.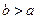 .
.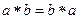 , то операция называется коммутативной, и соответственно, группоид - коммутативным.
, то операция называется коммутативной, и соответственно, группоид - коммутативным.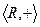 4.
4. 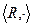 коммутативные группоиды.
коммутативные группоиды.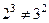 , есть и много других примеров.
, есть и много других примеров.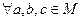 верно
верно 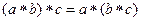 , то операция называется ассоциативной, и соответственно, группоид - ассоциативным (в таком случае его называют полугруппой).
, то операция называется ассоциативной, и соответственно, группоид - ассоциативным (в таком случае его называют полугруппой).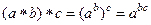
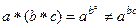 , так как в общем случае
, так как в общем случае 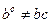 .
.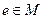 , что
, что 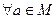 выполняется
выполняется 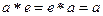 , то
, то 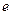 называется нейтральным элементом этого группоида.
называется нейтральным элементом этого группоида.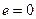 .
.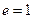 .
.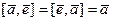 .
. 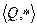 , операция
, операция 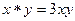 . Тогда
. Тогда 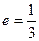 .
. 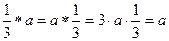 .
.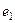 и
и 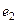 . Если мы умножим их между собой, то должно быть во-первых
. Если мы умножим их между собой, то должно быть во-первых 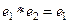 , так как
, так как 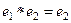 , так как
, так как 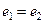 .
. 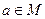 . Элемент
. Элемент 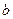 называется симметричным относительно
называется симметричным относительно 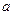 , если
, если 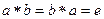 .
.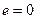 , симметричный это противоположный элемент
, симметричный это противоположный элемент 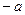 .
.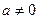 существует
существует 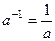 .
.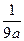 , так как
, так как 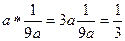 .
.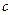 . Тогда
. Тогда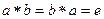 ,
, 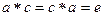 . Рассмотрим равенство
. Рассмотрим равенство 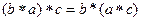 , из него следует, что
, из него следует, что 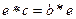 , но тогда
, но тогда 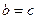 .
. 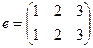
 с заданной на нём бинарной операцией
с заданной на нём бинарной операцией  называется группой, если:
называется группой, если: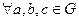
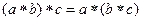
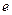 , то есть
, то есть 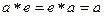
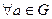
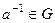 , т.е.
, т.е. 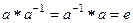 .
.  ,
,  ,
, 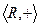 - «аддитивные» группы (по сложению).
- «аддитивные» группы (по сложению).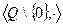 ,
, 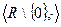 - «мультипликативные» группы (по умножению).
- «мультипликативные» группы (по умножению).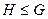 группы
группы 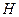 является группой относительно операции, введённой в группе
является группой относительно операции, введённой в группе 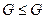 .
. .
.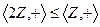 , все чётные числа. 0 нейтральный как в самой
, все чётные числа. 0 нейтральный как в самой 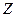 , так и в подгруппе.
, так и в подгруппе.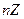 .
. 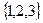 подгруппой не является, т.к. результат сложения может быть и больше 3, т.е. выводит за пределы этого множества.
подгруппой не является, т.к. результат сложения может быть и больше 3, т.е. выводит за пределы этого множества.
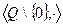
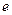 , это 1. Для каждого есть обратный. Для 2 это 3, для 3 это 2. В каждой строке (и каждом столбце) перестановка из трёх различных чисел.
, это 1. Для каждого есть обратный. Для 2 это 3, для 3 это 2. В каждой строке (и каждом столбце) перестановка из трёх различных чисел. 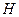 сама является группой, то
сама является группой, то 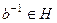 ,
, 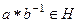 .
. 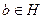 , то
, то 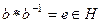 .
. 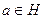 , обратный также принадлежит, ведь
, обратный также принадлежит, ведь 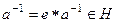 . □
. □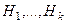 - подгруппы группы
- подгруппы группы 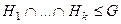 тоже подгруппа.
тоже подгруппа.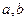
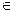
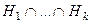 , то
, то 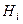 .
. 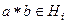 (всем), а значит, их пересечению. Кроме того,
(всем), а значит, их пересечению. Кроме того, 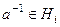 для всех номеров
для всех номеров 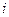 , а значит, тоже
, а значит, тоже 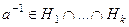 . В итоге,
. В итоге, 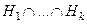 подгруппа. □
подгруппа. □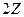 и
и 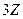 , а их пересечение
, а их пересечение 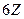 - все числа, кратные 6.
- все числа, кратные 6.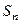 называется симметрической группой степени n. Число элементов
называется симметрической группой степени n. Число элементов 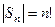
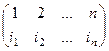 ,
, 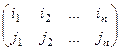 ,
, 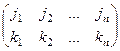 .
.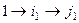 а затем
а затем 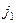 переходит в
переходит в 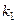 , в итоге
, в итоге 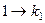 .
.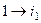 а
а 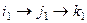 в результате композиции 2-й и 3-й подстановок, в итоге опять
в результате композиции 2-й и 3-й подстановок, в итоге опять 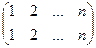 .
.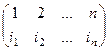 то обратный
то обратный 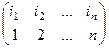 , где в верхней строке все n разных чисел и их можно расставить по порядку.
, где в верхней строке все n разных чисел и их можно расставить по порядку. 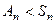 - группа всех чётных подстановок. Кол-во элементов
- группа всех чётных подстановок. Кол-во элементов 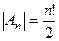 .
.
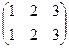
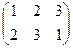
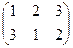 вращения
вращения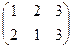
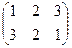
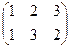 зеркальные отражения
зеркальные отражения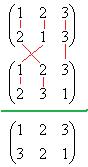
 называется группой Диэдра. Для
называется группой Диэдра. Для 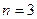 (в случае треугольника) она совпадает с группой всех подстановок,
(в случае треугольника) она совпадает с группой всех подстановок,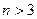 , уже
, уже 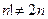 .
. 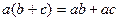 ,
, 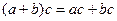 .
.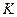 - множество, на котором заданы две бинарные операции (как правило, сложение и умножение), удовлетворяющие условиям:
- множество, на котором заданы две бинарные операции (как правило, сложение и умножение), удовлетворяющие условиям: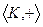 абелева группа
абелева группа 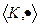 полугруппа (т.е. только ассоциативность)
полугруппа (т.е. только ассоциативность)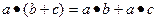 ,
, 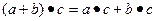 .
. называется кольцом.
называется кольцом. ,
, 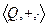 ,
, 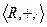 коммутативные кольца с единицей.
коммутативные кольца с единицей.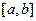 , можно поточечно складывать и умножать.
, можно поточечно складывать и умножать.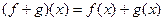 ,
, 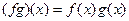 .
.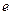 по сложению - тождественно нулевая функция
по сложению - тождественно нулевая функция 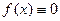 .
. 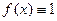 .
.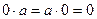 .
. 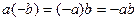 .
.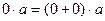 =
= 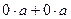 , вычтем
, вычтем 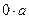 из обеих частей равенства, получим
из обеих частей равенства, получим 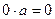 .
. 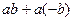 =
= 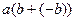 =
= 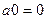
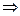
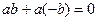
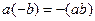 .
.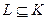 называется подкольцом, если оно само образует кольцо относительно операций, заданных в кольце
называется подкольцом, если оно само образует кольцо относительно операций, заданных в кольце 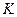 .
.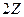 подкольцо в
подкольцо в 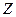 ,
, 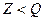 ,
, 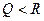 .
.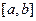 функции - подкольцо в кольце всех (по поточечному умножению, см. пример был выше).
функции - подкольцо в кольце всех (по поточечному умножению, см. пример был выше).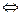
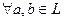 :
: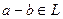 2)
2) 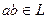 .
. 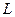 является подгруппой по сложению, тогда для любого
является подгруппой по сложению, тогда для любого 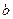 элемент
элемент 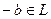 , а значит и
, а значит и 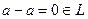 , а тогда и
, а тогда и 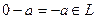 , то есть для каждого элемента противоположный тоже
, то есть для каждого элемента противоположный тоже 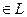 , т.е.
, т.е. 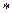 ).
).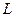 полугруппа.
полугруппа.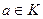 называется обратимым, если
называется обратимым, если 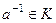 .
. 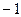 .
. или
или  обратимые элементы все, кроме 0.
обратимые элементы все, кроме 0.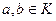 ,
, 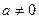 ,
, 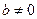 , но при этом
, но при этом 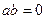 , то
, то 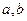 называются делителями нуля.
называются делителями нуля.
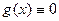 на
на 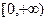 . Тогда
. Тогда 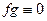 на всей числовой оси.
на всей числовой оси.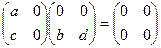 .
. обратим, и пусть всё же он является делителем 0, тогда есть какой-то
обратим, и пусть всё же он является делителем 0, тогда есть какой-то  , что
, что 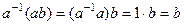 ,
,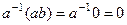 , тогда
, тогда 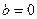 .
.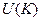 ).
). 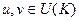 то
то 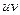 тоже обратим, т.е.
тоже обратим, т.е. 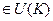 . Докажем, что обратный имеет такой вид:
. Докажем, что обратный имеет такой вид: 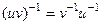 .
.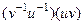 =
= 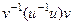 =
= 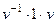 =
= 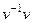 = 1.
= 1.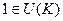 , ведь сам элемент 1 обратим, и обратный к нему тоже 1.
, ведь сам элемент 1 обратим, и обратный к нему тоже 1.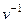 , то он автоматически обратим, обратный к нему это исходный
, то он автоматически обратим, обратный к нему это исходный 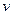 . □
. □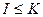 называется идеалом, если
называется идеалом, если 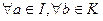
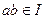 .
. 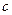 , образуют идеал. Если умножить произвольную функцию на такую, то произведение приобретает свойство
, образуют идеал. Если умножить произвольную функцию на такую, то произведение приобретает свойство 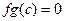 .
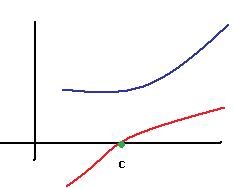
. 
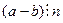 .
. 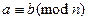 .
. 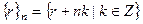 - класс вычетов по модулю n.
- класс вычетов по модулю n. 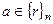 означает, что
означает, что 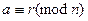 .
. 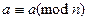 . Рефлексивность
. Рефлексивность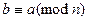 . Симметричность
. Симметричность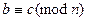
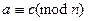 . Транзитивность
. Транзитивность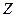 , и
, и 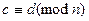
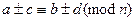
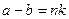 ,
, 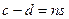 тогда
тогда 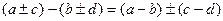 =
=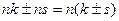 , то есть снова делится на n.
, то есть снова делится на n. 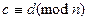
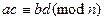
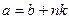 ,
, 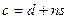
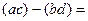
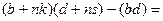
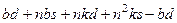 =
=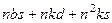 , это делится на n.
, это делится на n.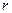 называется представителем класса
называется представителем класса 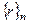 .
. 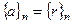 .
.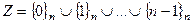
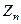 - множество всех классов вычетов по модулю n. Введём на этом конечном множестве из n элементов операции сложения и умножения:
- множество всех классов вычетов по модулю n. Введём на этом конечном множестве из n элементов операции сложения и умножения: 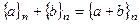 ,
, 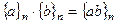 .
.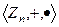 . Это коммутативное кольцо с единицей.
. Это коммутативное кольцо с единицей.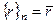 .
. 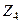 =
= 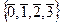 .
. 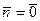 в
в 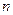 само делится на
само делится на