
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Взаимосвязь определителей большего и меньшего порядка. Разложение по строке. ⇐ ПредыдущаяСтр 6 из 6
Запишем разложение определителя порядка 3.
Вынесем за скобку элементы первой строки (они есть в 2 из 6 слагаемых): То, что получилось в скобках, называют алгебраическими дополнениями элементов соответственно Выражение в 1-й скобке
Заметим, что
Если для элемента Мы видим, что в одних случаях алгебраическое дополнение равно минору, а где-то противоположно ему по знаку. Взаимосвязь алгебраических дополнений и миноров для произвольных i,j:
Итак, определители можно вычислять разложением по строке:
Разложение возможно по любой строке или по любому столбцу. Так, например, в той же рассмотренной ранее записи можно собрать пары слагаемых, содержащих
Лемма. Доказательство. 1) Если для произвольного определителя 2) Если рассмотреть сумму
3) Общий случай. Рассмотрим сумму из
Теорема 1. Сумма всех произведений элементов какой-либо строки (столбца) матрицы на их алгебраические дополнения равна определителю матрицы: Доказательство. Каждое алгебраическое дополнение состоит из В итоге получим
Теорема 2. Если матрица треугольная, то Доказательство. Пусть дан определитель Если разложить его по первому столбцу, где всего один ненулевой элемент и остальные
для него получается аналогичное действие, тогда на следующем шаге получаем Замечание. Для диагональных матриц верен такой же факт, ведь диагональная это частный случай треугольной.
Пример.
Приведение к треугольному виду очень часто используется для вычисления определителей. Метод Гаусса, который будет подробно изучен в теме «системы уравнений», в полной мере может применяться и для вычисления определителей. Если обнулить элементы ниже главной диагонали, то вычисление определителя сильно упростится. Теорема 3. Сумма всех произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) равна 0: Доказательство. Если числа i-й строки умножаются на алгебраические дополнения к клетке на месте (1,1), (1,2),... (1,n) (ведь алгебраические дополнения не зависят от того, какое число в этой клетке было, а только от расположения), то это всё равно, что в 1-ю строку поставить копии чисел
Но такой определитель равен 0, так как две строки одинаковы. Обобщим метод разложения по строке. Введём понятие дополняющего минора и алгебраического дополнения к минору, а не к элементу. Если выбрать какие-либо
Теорема 4. Формула взаимосвязи минора и алгебраического дополнения: Доказательство. 1) Пусть исходный минор расположен в верхнем левом углу.
Все те члены определителя матрицы, в которых есть элементы этих миноров Причём перестановки, их задающие, содержат числа В этом случае, 2) Пусть минор
= Таким образом, чтобы вычислить алгебраическое дополнение к минору Произведение
Теорема 5 (Лапласа). Пусть в определителе порядка n произвольно выбрано k строк. Тогда сумма произведений всех миноров k-го порядка, содержащихся в выбранных строках, на их алгебраические дополнения, равна Доказательство. Количество миноров, содержащихся в k строках, равно числу сочетаний Для каждого из них получится сумма
Теорема 5 даёт возможность быстро считать определители блочно-диагональных и блочно-треугольных матриц. Например, для примера ниже - нет необходимости искать все 24 набора, достаточно вычислить так:
(В первых двух строках - всего один минор порядка 2).
Теорема 6. Определитель произведения квадратных матриц порядка n равен произведению определителей: Доказательство. Построим такую вспомогательную матрицу порядка 2n:
По теореме Лапласа, её определитель равен произведению двух миноров порядка n, то есть Теперь преобразуем матрицу, складывая столбцы (что, очевидно, не ведёт к изменению определителя). К
но это 1-й столбец произведения матриц: Аналогичными действиями обнуляем
Получается, что определитель этой матрицы равен Итак,
§ 3. Обратная матрица. Определение. Матрица называется вырожденной, если Определение. Пусть Обозначение: Обратная матрица обозначается
Замечание. Для чисел, которые являются матрицами порядка 1, обратный элемент вычисляется известным образом, например Докажем, что не существует различных «обратной слева» и «справа» матриц. Так как коммутативность в общем случае не выполняется, то вовсе не очевидно, что обратная матрица единственна, ведь можно предположить, что левая обратная и правая обратная - различны. Лемма. Если Доказательство. Пусть Но тогда получается
Итак, Теорема 1. Обратная матрица Доказательство. Для доказательства рассмотрим
|
|||||||
|
Последнее изменение этой страницы: 2020-11-28; просмотров: 84; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.162.247 (0.056 с.) |
 =
=  .
.  .
. .
.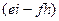 называется алгебраическим дополнением к элементу
называется алгебраическим дополнением к элементу 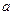 , соответственно
, соответственно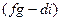 - алгебраическим дополнением к
- алгебраическим дополнением к 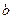 ,
, 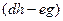 - алгебраическим дополнением к
- алгебраическим дополнением к 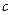 .
. ,
, 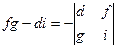 ,
,  .
.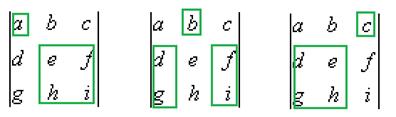
 и вычеркнуть всю строку и весь столбец, где он находится, образуется подматрица порядка (n-1). Определитель подматрицы порядка (n-1), которая получилась путём вычёркивания строки номер i и столбца номер j, называется дополняющим минором к элементу
и вычеркнуть всю строку и весь столбец, где он находится, образуется подматрица порядка (n-1). Определитель подматрицы порядка (n-1), которая получилась путём вычёркивания строки номер i и столбца номер j, называется дополняющим минором к элементу  . Всего таких миноров
. Всего таких миноров 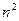 , например для матрицы 3 порядка их будет 9 штук. Минор, соответствующий элементу
, например для матрицы 3 порядка их будет 9 штук. Минор, соответствующий элементу 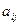 , обозначается
, обозначается 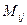 .
.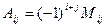 , то есть знаки меняются в шахматном порядке, для верхнего левого элемента
, то есть знаки меняются в шахматном порядке, для верхнего левого элемента  знак «+».
знак «+».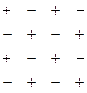
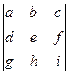 =
= 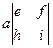
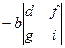
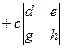 .
. и точно так же вынести за скобку, получится
и точно так же вынести за скобку, получится 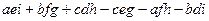 =
=  =
=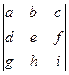 =
= 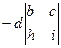

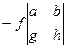 здесь чередование знака начинается с минуса, что и должно быть в соответствии с шахматным порядком, о чём сказано выше.
здесь чередование знака начинается с минуса, что и должно быть в соответствии с шахматным порядком, о чём сказано выше.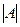 собрать отдельно все
собрать отдельно все 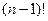 членов определителя, в составе которых присутствует
членов определителя, в составе которых присутствует  , и вынести за скобку
, и вынести за скобку  , то в скобке получится дополнящий минор (без смены знака). Это объясняется тем, что каждый из членов определителя в такой сумме задаётся перестановкой, имеющей 1 на первом месте:
, то в скобке получится дополнящий минор (без смены знака). Это объясняется тем, что каждый из членов определителя в такой сумме задаётся перестановкой, имеющей 1 на первом месте: 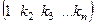 . Число инверсий в ней совпадает с числом инверсий перестановки
. Число инверсий в ней совпадает с числом инверсий перестановки 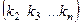 , так как 1 ни с каким числом инверсию не образует.
, так как 1 ни с каким числом инверсию не образует. членов определителя, в составе которых присутствует
членов определителя, в составе которых присутствует 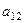 , то им соответствуют перестановки вида
, то им соответствуют перестановки вида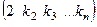 ведь в 1-й строке число взято из 2-го столбца. Число инверсий в ней ровно на 1 больше, чем в перестановке
ведь в 1-й строке число взято из 2-го столбца. Число инверсий в ней ровно на 1 больше, чем в перестановке 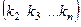 , так как среди чисел
, так как среди чисел 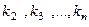 есть число 1, и оно образует инверсию с числом 2, расположенным на первом месте.
есть число 1, и оно образует инверсию с числом 2, расположенным на первом месте. членов определителя, в составе которых присутствует
членов определителя, в составе которых присутствует 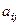 . Меняя строки и столбцы, можно добиться того, что это число окажется на месте
. Меняя строки и столбцы, можно добиться того, что это число окажется на месте  . Для этого нужно
. Для этого нужно 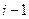 раз поменять строку с соседней сверху, а затем
раз поменять строку с соседней сверху, а затем 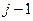 раз столбец, где было это число, с соседним слева. При этом будет совершено
раз столбец, где было это число, с соседним слева. При этом будет совершено  операций, то есть исходный определитель умножился бы на
операций, то есть исходный определитель умножился бы на  , что равно
, что равно 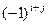 . Поэтому
. Поэтому  .
.  .
.  . По лемме,
. По лемме, 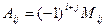 .
. 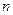 сумм по
сумм по 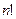 . Причём эти множества взаимно не пересекающиеся: для первых
. Причём эти множества взаимно не пересекающиеся: для первых 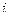 -й строке выбираем из 1-го столбца, в следующих из 2-го и т.д.
-й строке выбираем из 1-го столбца, в следующих из 2-го и т.д.  .
. .
. нулей, то сразу переходим к минору меньшего порядка:
нулей, то сразу переходим к минору меньшего порядка: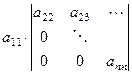 + 0 +... + 0.
+ 0 +... + 0.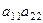 умножаются на определитель треугольной матрицы, у которой угловой элемент
умножаются на определитель треугольной матрицы, у которой угловой элемент  . Продолжая этот процесс, получим
. Продолжая этот процесс, получим  .
. 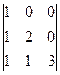 =
=  =
= 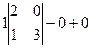 =
= 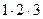 = 6.
= 6. .
.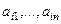 и затем вычислить определитель, содержащий две одинаковые строки:
и затем вычислить определитель, содержащий две одинаковые строки: 
 строк и
строк и  столбцов, на пересечении образуется минор порядка
столбцов, на пересечении образуется минор порядка 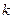 , обозначим его
, обозначим его 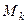 . Если вычеркнуть все эти
. Если вычеркнуть все эти  . Её определитель называется дополняющим минором к исходному минору, обозначим
. Её определитель называется дополняющим минором к исходному минору, обозначим 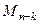 . Если выбрать в записи определителя всей матрицы те члены определителя, которые содержат элементы исходного выбранного минора порядка
. Если выбрать в записи определителя всей матрицы те члены определителя, которые содержат элементы исходного выбранного минора порядка  , где
, где  , то есть сумма всех номеров выбранных строк и столбцов исходного минора.
, то есть сумма всех номеров выбранных строк и столбцов исходного минора. докажем, что в этом случае дополняющий минор в точности равен алгебраическому дополнению.
докажем, что в этом случае дополняющий минор в точности равен алгебраическому дополнению.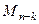 , составляют
, составляют  в точности слагаемых.
в точности слагаемых.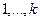 в каком-то порядке на первых
в каком-то порядке на первых  до
до 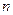 на последних
на последних  местах. Ни одно число из множества
местах. Ни одно число из множества 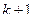 ,...,
,...,  , являющееся членом определителя
, являющееся членом определителя  из определителя
из определителя  очевидно, чётное число.
очевидно, чётное число.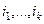 и столбцов с номерами
и столбцов с номерами 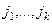 . Чтобы переместить его в левый верхний угол, нужно сначала, например, строку
. Чтобы переместить его в левый верхний угол, нужно сначала, например, строку 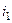 переместить на 1-е место, для чего будет нужно
переместить на 1-е место, для чего будет нужно 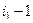 транспозиций соседних строк. Затем аналогично сделать с
транспозиций соседних строк. Затем аналогично сделать с 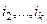 . Понадобится
. Понадобится 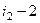 действий, чтобы строка с номером
действий, чтобы строка с номером 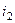 перешла на 2-е место, затем вплоть до того, что
перешла на 2-е место, затем вплоть до того, что  на месте k. А после этого такие же действия со столбцами. Общее количество действий:
на месте k. А после этого такие же действия со столбцами. Общее количество действий:
 . Последнее вычитаемое - чётное, тогда чётность всего полученного числа совпадает с чётностью числа
. Последнее вычитаемое - чётное, тогда чётность всего полученного числа совпадает с чётностью числа 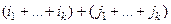 .
. , где
, где  содержит
содержит 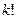
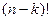 членов исходного определителя
членов исходного определителя 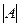 .
. 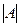 .
.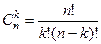 =
=  .
.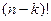 членов определителя исходной матрицы
членов определителя исходной матрицы 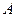 . Тогда
. Тогда 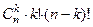 =
= 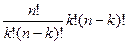 =
= 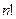 членов исходного определителя. При этом именно они все учтены, так как при таком разложении нет повторов: среди всех миноров, выбранных в
членов исходного определителя. При этом именно они все учтены, так как при таком разложении нет повторов: среди всех миноров, выбранных в  =
= 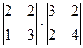 =
= 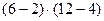 =
= 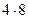 = 32.
= 32.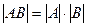 .
. .
. , так как в верхних n строках других миноров, отличных от нуля, нет.
, так как в верхних n строках других миноров, отличных от нуля, нет.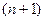 -у столбцу прибавим 1-й, домноженный на коэффициент
-у столбцу прибавим 1-й, домноженный на коэффициент 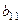 , затем 2-й, домноженный на
, затем 2-й, домноженный на  , и т.д. до n-го, домноженного на
, и т.д. до n-го, домноженного на 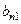 . После этого та часть
. После этого та часть 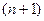 -го столбца, которая ниже n-й строки, станет состоять из нулей. А в верхних n строках получится такая часть столбца:
-го столбца, которая ниже n-й строки, станет состоять из нулей. А в верхних n строках получится такая часть столбца: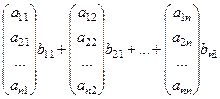 =
= 
 .
. 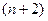 -й столбец ниже n-й строки, тогда в верхней части получается 2-й столбец из произведения
-й столбец ниже n-й строки, тогда в верхней части получается 2-й столбец из произведения  получится матрица, состоящая из блоков:
получится матрица, состоящая из блоков:  . Её определитель равен произведению двух миноров:
. Её определитель равен произведению двух миноров: 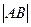 и
и  , домноженному на
, домноженному на 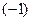 в степени
в степени  , так как это сумма номеров строк и столбцов минора
, так как это сумма номеров строк и столбцов минора  . При этом
. При этом 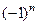 .
. 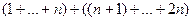 =
= 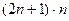 .
.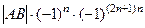 =
= 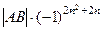 =
= 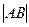 , так как
, так как 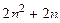 чётно.
чётно.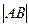 .
.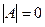 , и невырожденной, если
, и невырожденной, если  .
.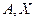 - квадратные матрицы. Если
- квадратные матрицы. Если  то
то 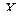 называется обратной матрицей для матрицы
называется обратной матрицей для матрицы  .
.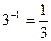 ,
, 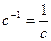 .
.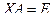 и
и 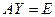 , то
, то  .
. 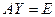 . По закону ассоциативности, можно записать такое равенство:
. По закону ассоциативности, можно записать такое равенство:  .
.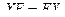 , то есть
, то есть 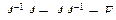 . Но оказывается, что не для любой квадратной матрицы существует обратная.
. Но оказывается, что не для любой квадратной матрицы существует обратная.  существует тогда и только тогда, когда А невырожденная.
существует тогда и только тогда, когда А невырожденная. . Если
. Если 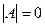 то
то  , то есть существовало бы такое число, которое при умножении на 0 даёт результат 1, но это невозможно. Получили противоречие.
, то есть существовало бы такое число, которое при умножении на 0 даёт результат 1, но это невозможно. Получили противоречие.


