
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Умножение квадратных матриц.Содержание книги Поиск на нашем сайте
В этом случае размеры всегда согласованы, и произведение - это тоже матрица
1) Не выполняется закон коммутативности 2) Ассоциативность выполняется (рассматривали на практике).
Существует такая матрица, которая во множестве матриц обладает свойством, аналогичным 1 во множестве чисел, то есть Единичная матрица Е. Строение: 2-го порядка:
(Аналог среди матриц первого порядка: число 1). Итак, Здесь может возникать естественный вопрос, зачем умножение ввели именно таким непростым образом, и почему нельзя было определить его тоже покомпонентно для пары матриц размера При таком способе умножения матриц, как мы ввели выше, выполняется важное свойство:
Свойства действий над матрицами: Коммутативность: Коммутативность по умножению не выполняется (говорили ранее). Свойства, связанные с ассоциативностью: 1. 2. 3. Свойства, связанные с дистрибутивностью: 1. 3. Множество прямоугольных матриц образует линейное пространство над полем R. Множество квадратных матриц порядка n можно умножать друг на друга, это множество образует кольцо. Таким образом, для квадратных матриц порядка n заданы 3 операции - сложение, умножение на константу, и умножение матриц. Такое множество с 3 операциями называют алгеброй матриц.
Определители. Понятие определителя 2-го порядка. Если дана матрица Обозначается: (произведение элементов главной диагонали, минус произведение элементов побочной диагонали).
Геометрический смысл: модуль определителя равен площади параллелограмма, сторонами которого являются 2 вектора, координаты которых расположены по строкам (либо столбцам) матрицы.
Если бы мы просто вычисляли площадь параллелограмма, построенного на векторах (2,1) и (1,2), где ни один вектор не расположен вдоль координатной оси, то понадобилось бы найти длину основания, затем высоту. А с помощью определителя, S вычисляется гораздо короче. Пример.
Оказывается, что модуль этой величины соответствует площади параллелограмма, построенного на основе двух векторов Докажем этот факт. Доказательство. Построим чертёж.
Перенесём закрашенную зелёным часть вниз, теперь мы уже получили такой прямоугольник, у которого одна сторона лежит на оси. Его высота Если векторы поменять местами, то определитель сменит знак,
Заметим, что при введении определителя, умножаемые элементы всегда расположены так, что 2 из них не находятся в одной строке или в одном столбце. Кстати, кроме главной и побочной диагонали, в матрице порядка 2 таких наборов элементов больше нет.
Если расположить первые n натуральных чисел 1,2,3,..., n в некотором порядке, возможно, не по возрастанию, а перепутать каким-то образом, то они образуют так называемую перестановку из n чисел. Каждый набор элементов, которые мы перемножаем в определителе 2 порядка, можно задать с помощью перестановки: главная диагональ (12) побочная диагональ (21). Большой прямоугольник в 1 строке, выбираем из 1 столбца, а когда он спустился во 2 строку, там из 2 столбца. Как на схеме:
таким путём мы как раз и получаем главную диагональ с помощью перестановки (12). Вспомним, что если большее число в перестановке расположено раньше, чем меньшее, то они образуют инверсию. В перестановке (12) инверсий нет, количество инверсий 0, то есть чётно. В перестановке (21) одна инверсия (то есть, их количество нечётно). Число
Определитель 3 порядка. Примеры, методы вычисления.
В записи определителя 3 порядка каждому элементу соответствует перестановка из 3 чисел.
Представьте себе прямоугольник, который сначала в 1-й строке, а затем спускается ко 2-й и 3-й, внутри него вправо и влево может двигаться квадрат, указывающий на какой-то из элементов. Запишем, в каком № столбца взяли элемент, когда находились в 1-й строке, затем так же во 2-й и 3-й. Например, для
для
(123) (231) (312) (321) (132) (213) Видим, что при этом учтены все возможные перестановки, количество которых 3! = 6. Рассмотрим подробнее, как знак определяется по перестановкам. Обозначим дугой каждую инверсию:
Если инверсий нечётное количество (1 или 3), то знак «-», если чётное (0 или 2) то «+». То есть, умножаем на Если изначально записать элементы матрицы с помощью индексов, то определитель имеет вид:
Индексы на вторых местах образуют такие перестановки:
Все рассмотренные наборы элементов, которые перемножаются между собой, обладают тем свойством, что никакие 2 из них не находятся в одной и той же строке либо одном и том же столбце. Таких наборов всего 6, и они все учтены. А для матрицы порядка 2 таких наборов всего 2, поэтому там определитель состоит всего из 2 слагаемых. Они не могут быть в одной строке или одном столбце, ведь перестановка состоит из разных чисел, то есть там нет одинаковых на двух местах, поэтому из одного и того же столбца 2 раза мы не выберем. Из одной строки тем более: находясь в некоторой строке, мы выбираем элемент только 1 раз.
Для матрицы 4 порядка потребуется найти все четвёрки элементов, так чтобы никакие два не оказывались в одной строке или одном столбце. Их будет 24 = 4!
Определители порядка n. Рассмотрим определение из математической энциклопедии:
Существует метод вычисления определителей с помощью треугольников, например, элемент
Обратите внимание, что главная диагональ
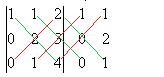
Запомнить метод вычисления определителей 3 порядка легче всего с помощью произведений по 3 параллельным линиям.
Надо дописать копии 1 и 2 столбца справа, и соединить по 3 параллельных линии: главная диагональ и параллельные ей (показаны зелёным цветом), затем побочная диагональ и параллельные ей (показаны красным). Умножить тройки чисел по 3 зелёным линиям, и взять их со знаком «+» а по красным прибавить со знаком «—». (Кстати, вместо столбцов справа можно дописать две строки снизу, и получится то же самое). Пример. Построим указанную схему (с помощью параллельных линий):
Ответ. 5.
|
||||||
|
Последнее изменение этой страницы: 2020-11-28; просмотров: 140; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.131.37.82 (0.011 с.) |

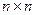 .
.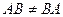 .
.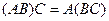 .
.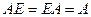 . Но, как мы видели, матрица из всех единиц этим свойством не обладает, а если единицы только по главной диагонали, а вокруг - нули, то такое свойство выполняется.
. Но, как мы видели, матрица из всех единиц этим свойством не обладает, а если единицы только по главной диагонали, а вокруг - нули, то такое свойство выполняется.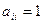 ,
, 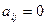 при
при 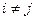 .
.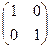 , 3 порядка:
, 3 порядка: 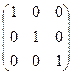
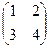
 , как и для сложения. Это мы тоже сейчас обоснуем подробнее.
, как и для сложения. Это мы тоже сейчас обоснуем подробнее.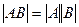 , то есть определитель произведения матриц равен произведению определителей. А это связано с важными геометрическими свойствами в дальнейшем. Если же умножение ввести покомпонентно, это свойство не выполняется.
, то есть определитель произведения матриц равен произведению определителей. А это связано с важными геометрическими свойствами в дальнейшем. Если же умножение ввести покомпонентно, это свойство не выполняется.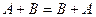 (по сложению).
(по сложению).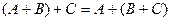
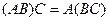
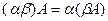
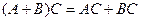 2.
2. 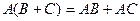
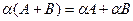 4.
4. 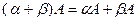
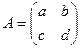 , то число
, то число 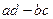 называется определителем этой матрицы.
называется определителем этой матрицы.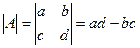 .
.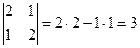 .
. 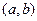 ,
, 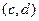 .
.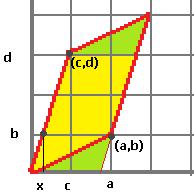
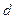 . Длина основания это разность
. Длина основания это разность 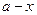 , где абсциссу
, где абсциссу 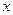 можно найти, вычислив с помощью пропорции, ведь вектор
можно найти, вычислив с помощью пропорции, ведь вектор 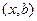 пропорционален вектору
пропорционален вектору 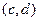 .
. 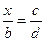
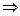
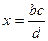 . Тогда произведение основания на высоты равно
. Тогда произведение основания на высоты равно 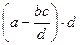 =
= 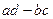 .
.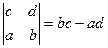 , тогда не сама величина, а её модуль равен площади параллелограмма.
, тогда не сама величина, а её модуль равен площади параллелограмма.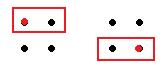
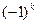 , где k - число инверсий, определяет знак соответствующего произведения, участвующего в построении определителя.
, где k - число инверсий, определяет знак соответствующего произведения, участвующего в построении определителя.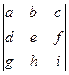 =
= 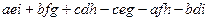 .
.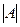 =
= 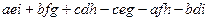
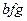 получится (231):
получится (231):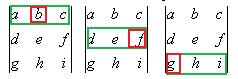
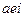 соответствует (123) и т.д. напишем под каждым элементом свою перестановку:
соответствует (123) и т.д. напишем под каждым элементом свою перестановку: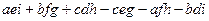
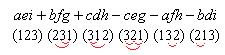
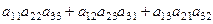
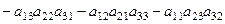
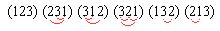

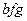 соответствует треугольнику:
соответствует треугольнику: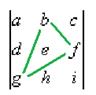
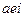 здесь - это средняя линия данного треугольника. Два треугольника, соответствующие произведениям со знаком плюс, это те, для которых главная диагональ является средней линией, а мо знаком минус - если побочная диагональ является средней линией.
здесь - это средняя линия данного треугольника. Два треугольника, соответствующие произведениям со знаком плюс, это те, для которых главная диагональ является средней линией, а мо знаком минус - если побочная диагональ является средней линией.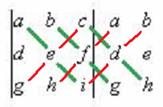
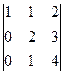 .
.
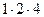 +
+ 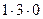 +
+ 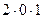
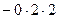
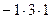
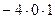 =
= 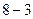 = 5.
= 5.


