
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение (через полную таблицу ):Содержание книги Поиск на нашем сайте
9) запишем заданное выражение в более простых обозначениях:
10) общий ход действий можно описать так: подставляем в эту формулу какое-нибудь значение (0 или 1) одной из переменных, и пытаемся определить, в каком столбце записана эта переменная; 11) например, подставим x = 0, при этом сразу получаем F = 0; видим, что переменная x не может быть ни в первом, ни во втором столбце (противоречие во 2-й строке):
а в третьем – может:
12) подставим x = 1, тогда 13) ищем такую строчку, где x = 1 и
14) как мы видели, в этой строке таблицы должно быть обязательно z = 1 и y = 0; поэтому z – в первом столбце, а y – во втором 15) Ответ: zyx. Решение (преобразование логического выражения, Дегтярева Е.В.): 1) Используя законы алгебры логики, а именно распределительный для операции «ИЛИ» (см. учебник 10 кл. 1 часть, стр. 185), запишем заданное выражение:
2) Поскольку добиться логической единицы в произведении сложнее, чем в сумме рассмотрим строки таблицы, где произведение равно 1(это 2-я, 4-я и 8-я строки); 3) Во 2-й строке Х обязательно должно быть равно 1. Поэтому Х может быть только в третьем столбце, в первых двух могут быть и Y, и Z.
4) Анализируя 4 строку приходим к выводу, что в первом столбце таблицы может быть только Z, во втором – Y.
5) В 8-й строке убеждаемся в верности своих рассуждений:
Т.о., немного упростив выражение, уменьшили количество рассматриваемых строк. 6) Ответ: zyx. Решение (преобразование логического выражения, СДНФ, В.Н. Воронков): 1) Рассмотрим строки таблицы, где функция равна 1
и построим логическое выражение для заданной функции, обозначив переменные через a, b и с (см. § 22 из учебника для 10 класса):
2) Упрощаем это выражение, используя законы алгебры логики: 3) Сравнивая полученное выражение с заданным
4) Ответ: zyx. Решение (сопоставление таблиц истинности, М.С. Коротков): 1) Рассмотрим строки таблицы, где функция равна 1, обозначив переменные через a, b и с
и сопоставим эти строки с теми строками таблицы истинности заданной функции
2) Сравнивая столбцы интересующих нас строк, определяем, что c = x (все три единицы в зеленых ячейках), b = y (один ноль и две единицы) и a = z (два ноля и единица). 3) Ответ: zyx.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-22; просмотров: 113; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.12.133 (0.009 с.) |

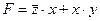
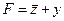 ; логическая сумма равна 0 тогда и только тогда, когда все слагаемые равны 0, это значит, что
; логическая сумма равна 0 тогда и только тогда, когда все слагаемые равны 0, это значит, что 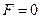 только в одном случае – при z = 1 и y = 0;
только в одном случае – при z = 1 и y = 0;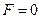 :
: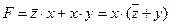 ;
;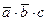
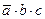
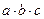

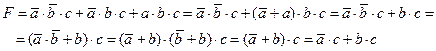
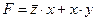 , находим, что a = z, b = y и c = x.
, находим, что a = z, b = y и c = x.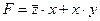 , где F = 1:
, где F = 1:


