
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение (разбиение на два слагаемых, А. Н. Носкин):Содержание книги Поиск на нашем сайте
1) запишем выражение в более понятной форме: 2) Каждое из слагаемых скобок должна быть равна 0, поэтому составим для каждой таблицу истинности. 3) Рассмотрим ((w ® z) Ù (y ® w)), а именно первую скобку (w ® z), она равна 0 при ситуации 1 ® 0, тогда y во второй скобке может быть любым
Теперь рассмотрим вторую скобку (y ® w), она равна 0 при ситуации 1 ® 0, тогда z во первой скобке может быть любым. Добавим эти значения в таблицу истинности, которая приведена выше.
4) Теперь рассмотрим ((w Ú y) º x). Эта скобка будет равна 0 при ((w Ú y) ≠ x). Составим таблицу истинности
Анализ этой таблицы показывает, что набора 001 (выделено цветом) быть не может иначе система будет равна 1 по скобке ((w ® z) Ù (y ® w)). 5) Сравним полученные таблицы истинности с исходной таблицей в задании:
6) x в таблице истинности во всех строках равен 0, тогда он соответствует второму столбцу, так как там нет ни одной единицы. Сразу заполним нулями.
7) w и y в таблице истинности имеют 2 и более единицы, а z всего 1, тогда z - это столбец 3. Заполним сразу 0.
8) Так как строки не повторяются, то в первой ячейке второй строки может быть только 0. Заполним ее.
9) Теперь проанализируем последнюю ячейку третьей строки. Ее значения могут быть 0 и 1. Предположим, что там 0, а в первом столбце w, тогда выражение примет вид ((1 Ú 0) º 0) Ú ((1 ® 1) Ù (0 ® 1)) – этого быть не может, так как выражение равно 1. Предположим, что там 1 и в первом столбце w, тогда выражение примет вид ((1 Ú 1) º 0) Ú ((1 ® 1) Ù (1 ® 1)) – этого быть не может, так как выражение равно 1. Таким образом в первом столбце w не может быть ни при каком случае. Там только y, ну а w отправляется в 4-й столбец. 10) Ответ: yxzw. Ещё пример задания: Р-18. Логическая функция F задаётся выражением (x Ú y) ® (y º z). На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно. Решение: 1) запишем выражение в более понятной форме: 2) для решения этой задачи используем свойство операции «импликация»: 3) в обеих строках приведённой части таблицы функция равна 0, поэтому везде · хотя бы одна из величин, x или y равна 1, что даёт · y и z различны, что даёт 4) поскольку значения в первых двух столбцах в первой строке равны 0, один из этих столбцов – это x 5) предположим, что x – это первый столбец:
тогда в обеих строках получаем 6) это значит, что x – это не первый, а второй столбец:
7) если при этом предположить, что первый столбец – это y, то в первой строке получаем 8) на всякий случай проверяем первую строку: 9) во второй строке условие 10) Ответ: zxy. Решение (построение части таблицы истинности, С.В. Логинова): 1) По свойству импликации функция имеет значение 0 тогда, когда в первой скобке получится 0, а во второй 1. Из этого следует что возможные сочетания для переменных x и y равны 01, 10, 11. 2) Вторая скобка равна 0, если y и z имеют разные значения. 3) Составим таблицу истинности для всех возможных вариантов.
4) Из получившейся таблицы истинности мы видим, что только одна строка этой таблицы содержит 2 нуля и одну 1 в исходных данных. Эта единица – переменная y, значит третий столбец y. Среди столбцов только один содержит два нуля – столбец z. Отсюда следует, что первый столбец – z. 5) Ответ: zxy
Решение (метод исключения, С.Н. Лукин, г. Москва): 1) всего возможно 6 вариантов решения задачи:
В процессе решения будем вычеркивать лишние варианты, пока не останется один-единственный. Также будем по возможности заполнять пустые клетки таблицы (по принципу «Чем меньше неопределенностей, тем лучше»). 2) используем следующее свойство импликации: выражение a ® b равно нулю тогда и только тогда, когда a =1 и b =0. В нашем примере a это левая скобка, b – правая. 3) теперь рассуждаем от противного. Пусть в пустой клетке первой строки таблицы истинности стоит ноль:
4) Тогда в любом из 6 вариантов решения получится x = 0 и y = 0, а значит (x Ú y)=0, что противоречит упомянутому свойству импликации. Значит, там стоит единица:
5) По той же причине в левых двух столбцах первой строки не могут находиться одновременно x и y. Это позволяет нам вычеркнуть два из шести вариантов решения:
Остаются 4 варианта:
6) Идем дальше. По упомянутому свойству импликации вторая скобка должна равняться 0, а значит y и z не должны совпадать. Это позволяет нам, погдядев на первую строку таблицы истинности, вычеркнуть еще два варианта решения: Остаются 2 варианта:
7) Получается, что в правом столбце обязательно стоит y. Начало положено. 8) Попробуем заполнить пустые клетки во второй строке таблицы истинности. Способов заполнения четыре: 00, 01, 10, 11. Первый из них мы рассмотрели выше, он отпадает. Второй отпадает, так как в этом случае две строки таблицы истинности будут совпадать, что противоречит условию задачи. Третий и четвертый способы приказывают нам иметь во втором столбце единицу. Спасибо и на этом:
9) Теперь рассмотрим первый из двух оставшихся вариантов решения (xzy), подставив сначала в пустую клетку ноль. Но ноль отпадает, так как x и y не могут одновременно равняться нулю. А единица отпадает, так как y и z не должны совпадать. Значит, отпадает и сам вариант решения xzy. Следовательно, решением задачи является единственный невычеркнутый вариант: zxy. 10) Из тех же соображений, что y и z не должны совпадать, в оставшуюся пустую клетку ставим единицу:
11) А теперь проверьте решение, подставив в выражение (x Ú y) ® (y º z) значения переменных из каждой строки таблицы. 12) Ответ: zxy. Решение (метод инверсии, А.Н. Носкин, г. Москва): 1) Известно, что если F = 0, то обратная её функция 2) Применим закон де Моргана и упростим:
3) тогда при тех же значениях аргументов функция
4) анализ формулы 5) Кроме того, этот анализ показывает, что в первой строке таблицы, в ее последнем столбце, не может быть 0, так как тогда значение функции не будет равно 1. На основе этого анализа таблица примет вид:
6) Анализ первой строки данной таблицы показывает, что в первых двух ячейках не может быть одновременно ни x, ни y. В этих ячейках рядом может быть только x и z, значит y находится в последней ячейке. 7) Во второй ячейке, второй строки не может быть 0, так как должны быть неповторяющиеся строки, а все нули быть не могут (не выполнится условие
8) Значит в оставшейся ячейке может быть только 0 или 1, а именно, во второй строке возможен набор 010 или 011. Простой анализ с учетом того, что в последнем столбце y, дает итоговый ответ – набор 011. 9) Ответ: zxy. Ещё пример задания: Р-17. Логическая функция F задаётся выражением x Ú y Ú (z Ù w). На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F ложна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно. Решение: 1) запишем выражение в более понятной форме: 2) анализ формулы
3) остается разобраться с двумя средними столбцами; обратим внимание на вторую строчку таблицы, в которой одна из оставшихся переменных равна 1, а вторая – 0; так как функция равна 0, то 4) Ответ: yzwx.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-22; просмотров: 149; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.45.90 (0.009 с.) |

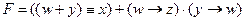
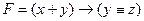
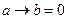 тогда и только тогда, когда a = 1 и b = 0
тогда и только тогда, когда a = 1 и b = 0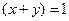 ;
;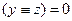
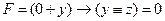 , откуда сразу следует, что есть единственная пара остальных переменных, удовлетворяющих условию задачи: y = 1, z = 0, и вторая строка олжна быть копией первой (второй подходящей пары y, z нет!), что противоречит условию
, откуда сразу следует, что есть единственная пара остальных переменных, удовлетворяющих условию задачи: y = 1, z = 0, и вторая строка олжна быть копией первой (второй подходящей пары y, z нет!), что противоречит условию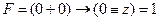 (при любом z!), что противоречит условию; поэтому первый столбец – это z, а третий – y
(при любом z!), что противоречит условию; поэтому первый столбец – это z, а третий – y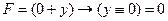 справедливо при y = 1
справедливо при y = 1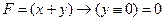 справедливо при x = 1 и y = 1 (что отличается от варианта в первой строке значением x)
справедливо при x = 1 и y = 1 (что отличается от варианта в первой строке значением x)



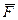 =1.
=1.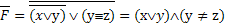
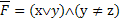 показывает, что для истинности функции
показывает, что для истинности функции 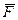 необходимо, чтобы значение в каждой скобке были равны 1.
необходимо, чтобы значение в каждой скобке были равны 1.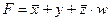
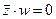 , откуда следует, что z = 1 и w = 0 (иначе произведение будет равно 1)
, откуда следует, что z = 1 и w = 0 (иначе произведение будет равно 1)


