Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение (построение таблицы с помощью электронных таблиц, П.Е. Финкель, г. Тимашевск)Содержание книги
Поиск на нашем сайте
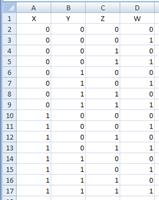
1) поскольку во время компьютерного экзамена есть возможность использовать электронные таблицы, можно построить таблицу истинности с их помощью 2) заполняем первую часть таблицы, перечисляя все комбинации переменных в порядке возрастания двоичного кода:
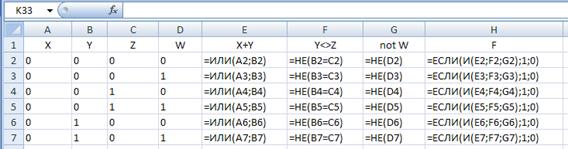
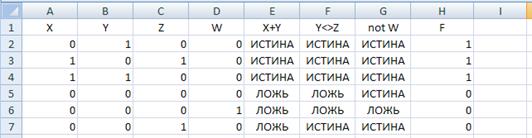
3) для каждой строчки определяем выражения, входящие в логическое произведение, а затем – значение функции:
4) сортируем строки таблицы по столбцу H по убываниию:
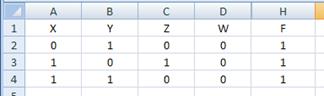
5) удаляем строки, где функция равна 0; можно также скрыть вспомогательные столбцы E, F, G:
6) дальше рассуждаем так же, как и при теоретическом решении 7) Ответ: zyxw. Решение (построение таблицы с помощью программы, А.С. Гусев, г. Москва, https://youtu.be/RRL1Wal9ImU): 1) поскольку во время компьютерного экзамена есть возможность использовать среды программирования, для построения частичной таблицы истинности (всех строк, при которых F=1) можно написать переборную программу на Python 2) перебор выполняем во вложенном цикле: for x in 0, 1: for y in 0, 1: for z in 0, 1: for w in 0, 1: # вычисление функции F # вывод (x, y, z, w), если F =1 3) для вычисления значения функции необходимо понимать, как логические операторы записываются на языке программирования; в Python их можно реализовать следующим образом: ∧ конъюнкция and ∨ дизъюнкция or отрицания not() ≡ тождество == ⊕ строгая дизъюнкция!= → импликация – для импликации в python оператора нет, но импликацию можно преобразовать в дизъюнкцию; например, a → b можно записать как a ∨ b, а это в свою очередь записать как not(a)or b 4) Запишем нашу функцию на языке программирования: F = (x or y) and not(y == z) and not(w) 5) чтобы выводить не полную таблицу истинности, а только те строки, в которых функция равна 1, добавим условие вывода: if F: # то же самое, что " if F == True:" print(x, y, z, w) 6) Приведём полную программу: Print('x y z w') for x in 0, 1: for y in 0, 1: for z in 0, 1: for w in 0, 1: F = (x or y) and not(y == z) and not(w) if F: print(x, y, z, w) 7) после запуска программы получаем все интересующие нас строки: X y z w 0 1 0 0 1 0 1 0 1 1 0 0 8) дальше рассуждаем так же, как и в приведённом выше теоретичеком решении 9) Ответ: zyxw. Решение (прямой перебор, А. Богданов): 1) в принципе, можно написать программу, которая сразу выдает решение этого задания прямым перебором вариантов 2) Часть 1: https://www.youtube.com/watch?v=yX5oSYtM5E0 3) Часть 2: https://www.youtube.com/watch?v=eSkrt4KrsmU 4) Ответ: zyxw. Ещё пример задания: Р-21. Логическая функция F задаётся выражением ((x Ù y) Ú (w ® z)) º (z º x). На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно. Решение (построение таблицы истинности для F = 1): 1) перепишем выражение, раскрыв импликацию по формуле 2) сначала предположим, что
3) так как 4) теперь пусть 5) используем распределительный закон:
6) этот единственный вариант, для которого
7) в остальных строчках должно вполняться равенство 8) предположим, что x – третий столбец, и в свободной ячейке – нуль:
9) при этом для остальных двух столбцов в этих строчках должно выполняться условие
10) чтобы разобраться с поcледними двумя столбцами снова вспомним, что при 11) Ответ: zywx Решение (А.Н. Носкин, заполнение исходной ТИ и анализ полной таблицы истинности для F = 1): 1) в выражении 4 логических переменных, тогда всех решений будет 16 (24).
2) подставим набор значений логических переменных и удалим все решения, которые не дают в ответе F = 1
Получаем 7 решений. Анализируя ТИ исходной функции видим, что набора 0 0 0 0 и 1 1 1 1 нет. Уберем их из ТИ решений.
3) В ТИ решений только одна строка имеет три нуля, тогда сравнивая с ТИ исходной функции видим, что 1 соответствует Y.
4) ДОЗАПОЛНИМ таблицу истинности исходной функции (желтая заливка) на основе анализа ТИ решений, а именно т.к больше строк с тремя «0» нет, то в первой строке в пустой ячейке будет «1». И раз нет больше строк с двумя «0», то в третьей строке пустые ячейки равны «1».
5) Анализируя 1ю строку выше приведенной таблице и ТИ решений видим, что строка с двумя «0» всего одна, из которых один нуль известен - это Y, тогда второй это – W;
6) Далее рассуждая видим, что в ТИ решений (кроме столбца Y) один «0» имеет – Х, тогда последний столбец – это Х, а первый столбец – Z. 7) Ответ: zywx Ещё пример задания: Р-20. Логическая функция F задаётся выражением ((x Ù y) Ú (y Ù z)) º ((x ® w) Ù (w ® z)). На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно. Решение (построение таблицы истинности для F = 1): 1) запишем выражение в более понятной форме: 2) попробуем найти все сочетания переменных, при которых функция равна 1 (их должно быть не очень много) 3) при x = 0 получаем 4) пусть теперь ещё z = 0, тогда 5) пусть теперь x = 0 и z = 1, тогда 6) из 4 и 5 получаем такие строки в таблице истинности исходной функции:
7) остаётся рассмотреть случай, когда x = 1, при этом 8) учитываем, что 9) преобразуем импликацию 10) для y = 0 это выражение истинно при (w, z) = (0,0), (0,1) и (1,0), а для y = 1 – только при w = z = 1, это даёт ещё 4 строки в таблице истинности
11) итак, у нас есть 8 строк в таблице истинности, где функция равна 1:
попробуем сопоставить их с заданными в условии строками:
12) замечаем, что есть одна характерная строка с тремя единицами; кроме того, поскольку все строки различны, в одной из пустых ячеек должен стоять 0, а во второй – 1 13) в полученной нами таблице видим единственную строку с тремя единицами, что сразу позволяет определить, что первый столбец – это x, который всегда равен 0:
14) теперь из оставшихся двух строк остаётся найти 2 строки, значения которых различаются только в одном столбце; под это условие подходит только пара двух верхних строк, они различаются в столбце y – из исходной таблицы видим, что это 4-й столбец 15) также из исходной таблицы видим, что во втором столбце в этих двух строках единицы – это w, тогда третий столбец – это z 16) Ответ: xwzy. Решение (А.Н. Носкин, построение таблицы истинности для F = 1): 1) запишем выражение в более понятной форме: 2) вынесем y за скобки: F = (y*(x+z) ≡ ((x→w)*(w→z)) 3) F = 1, при 0=0 и 1=1. Тогда составим ТИ для левой части выражения равные 0 и 1.
4) Объединим эти таблицы, подключим переменную w и уберем из таблицы строки, при которых F=0 после подключения переменной w.
5) Получилось 8 всевозможных решений. 6) Обратим внимание, что по условию у нас нет повторяющихся строк, но в таблице есть строки с тремя одинаковыми ячейками, тогда можно ДОЗАПОЛНИТЬ таблицу истинности исходной функции (желтая заливка) в одну из них вставив 0, в другую 1.
7) Анализ строк таблицы истинности исходной функции показывает: - строки, состоящей из четырех «1» нет, поэтому ее можно убрать (красная заливка); - только одна строка имеет в ячейках три единицы и один «0». И в ТИ всех решений (желтая заливка) этот «0» будет соответствовать Х в ТИ исходной функции.
8) Так как мы определили, что первый столбец соответствует Х и содержит только «0», то строки ТИ решений с «1» в столбце Х – удалим (синяя заливка)
и получим ТИ меньшего размера.
9) Анализ столбцов ТИ исходной функции показывает, что одна «1» в третьем столбце соответствует Z, а в третьей строке ТИ исходной функции две неизвестные переменные противоположны «0» и «1», что соответствует W и Y, так как X и Z уже определены и равны «0» (зеленая заливка)
10) Ответ: xwzy. Ещё пример задания: Р-19. Логическая функция F задаётся выражением ((w Ú y) º x) Ú ((w ® z) Ù (y ® w)). На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно. Решение: 1) запишем выражение в более понятной форме: 2) попробуем найти все сочетания переменных, при которых функция равна 0 (их должно быть не очень много) 3) выберем для начальной подстановки переменную, которая чаще всего встречается в выражении и поэтому подстановка её значения даст наибольшую информацию; у нас это переменная w 4) подставим сначала w = 0, а затем w = 1, и таким образом построим все строки таблицы истинности, где функция равна нулю 5) при w = 0 получаем поскольку 6) для того, чтобы сумма была равна 0, оба слагаемых должны быть равны 0, так что
7) таким образом, при w = 0 получаем y = 1, x = 0, а значение z может быть любое; это даёт две строки в таблице истинности:
8) теперь рассмотрим случай, когда w = 1: получаем поскольку 9) для того, чтобы сумма была равна 0, оба слагаемых должны быть равны 0, так что
10) таким образом, при w = 1 получаем x = 0, z = 0, а значение y может быть любое; добавляем ещё две строки в таблицу истинности:
11) сравниваем эту таблицу с таблицей в задании:
12) две единицы могут быть только в столбцах y и w, поэтому это столбцы 1 и 4 13) кроме этих столбцов единственная единица может быть в столбце z, поэтому столбец 3 – это z 14) при z = 1 должно быть y = 1, поэтому столбец 1 – это y, а столбец 4 – это w 15) остаётся столбец 2 – это x 16) Ответ: yxzw.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-22; просмотров: 468; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.011 с.) |

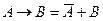 :
: 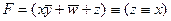
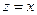 ; в этом случае получаем
; в этом случае получаем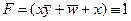
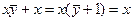 , получим
, получим 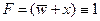 ; при этом значение y может быть любым (1 или 0)
; при этом значение y может быть любым (1 или 0)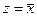 , тогда получаем
, тогда получаем 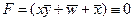
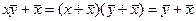 , так что
, так что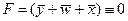 , откуда сразу следует
, откуда сразу следует 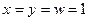 и
и 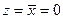 – единственный вариант!
– единственный вариант!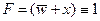 , а оно не может выполняться – при любом варианте в одной строке сумма
, а оно не может выполняться – при любом варианте в одной строке сумма 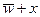 равна 0; значит x – последний столбец, и в первой строке z = 1:
равна 0; значит x – последний столбец, и в первой строке z = 1: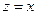 должно выполняться условие
должно выполняться условие 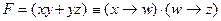
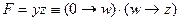 ; импликация с нулём в левой части всегда истинна (из лжи следует всё, что угодно), поэтому
; импликация с нулём в левой части всегда истинна (из лжи следует всё, что угодно), поэтому 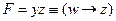
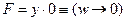 , что истинно при w = 1 и при любом y;
, что истинно при w = 1 и при любом y;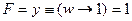 , что истинно при y = 1 и при любом w;
, что истинно при y = 1 и при любом w;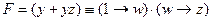
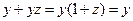 и
и 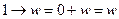 ; получаем
; получаем 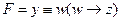
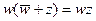 , так что
, так что 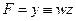
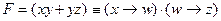
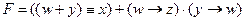
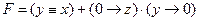
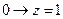 при всех z, имеем
при всех z, имеем 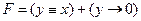
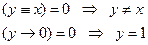
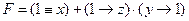
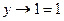 при всех y, имеем
при всех y, имеем