Комплексные числа и действия над ними.

 

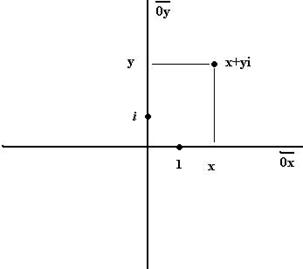
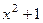       Система действительных чисел является неполной, так как не содержит корни некоторых многочленов, например . Если  квадратичное уравнение  имеет отрицательный дискриминант, то есть 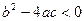, то на действительной оси нет ни одного корня. Однако существует система условных, обобщённых чисел, где и такие уравнения тоже имеют решения. Они называются комплексными числами и геометрически соответствуют точкам на плоскости, а известная ранее действительная ось - это горизонтальная ось Ох в данной плоскости. Введено абстрактное понятие «мнимая единица»  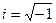обозначающая «квадратный корень из минус 1». При этом получается .

Геометрическая интерпретация. На плоскости, горизонтальная ось отождествляется со множеством действительных чисел, а мнимая ось, содержащая , перпендикулярна оси действительных чисел.

 

.

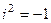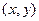Комплексные числа - ещё более абстрактное обобщение. Оно полезно при решении различных физических задач. Плоскость комплексных чисел есть расширение множества действительных чисел. Каждой точке на плоскости с координатами  можно поставить в соответствие комплексное число, состоящее из действительной и мнимой части: 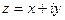. Проекция на действительную и мнимую ось называются действительной частью и мнимой частью комплексного числа. , .

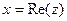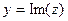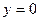Если , то число  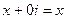это обычное действительное число.

Сложение и вычитание комплексных чисел определяется покоординатно, как для обычных векторов в плоскости.

 = .

Для вычитания аналогично:  = .

Умножение.

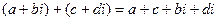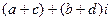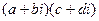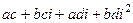 = , учитывая тот факт, что ,

получаем  = .

Таким образом, после раскрытия скобок, надо просто учесть  и привести подобные.

Пример.  =  = .

 

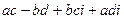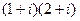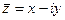Определение. число  называется сопряжённым к .

       Умножим два взаимно сопряжённых комплексных числа:

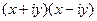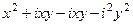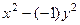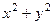 =  =  = , получилось действительное число. Мы заметили, что при умножении на сопряжённое мнимая часть станет 0. Этот факт можно использовать для процедуры деления. Если домножить на сопряжённое в знаменателе, то там получится действительное число, и это даст возможность разбить на сумму двух дробей. При этом, конечно, в числителе тоже домножаем на сопряжённое к знаменателю, чтобы дробь не изменилась.

= = =

Пример. Вычислить .

Решение. =  =  =  =  =

 

Поиск корней многочлена с отрицательным дискриминантом.

Пример. Найти корни уравнения .

Решение. ,  =  =  = .

Ответ. .

Кстати, как видно, получаются именно 2 взаимно сопряжённых корня.

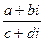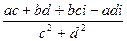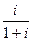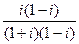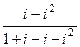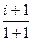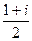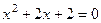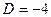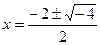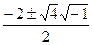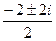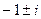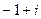Проверка. Подставим, например,  в уравнение.

 =  =  = .

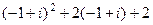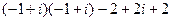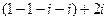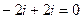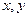Действительную и мнимую часть  для числа  можно выразить через .

Докажем такие формулы: ,

Доказательство.

Сложим  и .

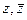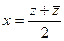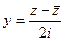
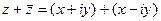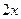 = , тогда .

Вычтем  и .

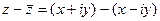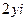 = , тогда .

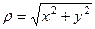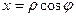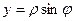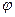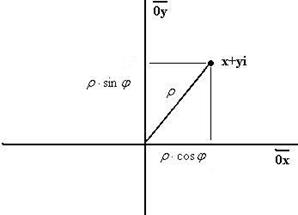
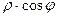Тригонометрическая форма комплексного числа.   Введём величину  тогда  можно представить в таком виде: ,  для некоторого , ведь геометрически в этом случае  - катеты прямоугольного треугольника, - его гипотенуза.

Абсцисса и ордината точки  на плоскости это проекции на оси, они равны  и 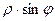 соответственно. Эти величины  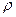и  и 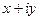есть полярные координаты точки на плоскости. Если записать комплексное число  с помощью введённых выше величин  и , получим: =  = .

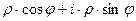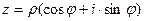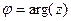
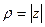Выражение  называется тригонометрической формой комплексного числа,  - его аргументом,  - модулем.

.

Понятие модуля согласуется с известным понятием, применявшимся раньше для отрицательных чисел: модуль - расстояние по кратчайшей линии до начала координат. 

Для любой точки  модуль вычисляется как  . Для вычисления аргумента верна формула 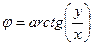  если точка в 4-й и 1-й четверти, либо 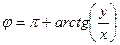, если во 2-й и 3-й четверти.

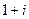Так, число  запишется в виде .

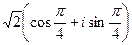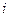Число  соответствует .

Если вычислить синус и косинус, то снова перейдём к обычной, «алгебраической» форме числа:

 =  = .

 

 

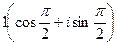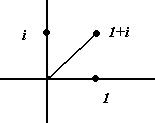
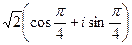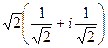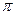Действительное число имеет аргумент 0 (если оно положительно) или  (если оно отрицательно).

 

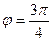Угол может определяться разными способами, так, например, вместо угла  во всех вычислениях для комплексных чисел в тригонометрической форме можно использовать 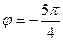, и это не будет ошибкой, так как тригонометрические функции повторяются через промежуток .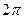