
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление несобственных интегралов по действительной оси
Если на комплексной плоскости особых точек лишь конечное количество, то существует самая дальняя из них (с наибольшим модулем). Тогда можно найти такой радиус По основной теореме о вычетах, интеграл по границе полукруга равен произведению
Тем самым, мы 1 раз обходим весь контур против часовой стрелки. Именно этим и объясняется, что надо рассматривать полукруг именно в верхней, а не нижней полуплоскости, а иначе движение по действительной оси получалось бы справа налево. Начиная с некоторого радиуса Теорема. Если Пример. Вычислить Во 2 семестре вычисляли такие несобственные интегралы,
А теперь покажем, как решить с помощью вычетов. Решение. Заметим, что степень числителя на 2 порядка больше, чем степеннь знаменателя, то есть Введём в рассмотрение функцию
Ответ.
3) Вычисление интегралов, содержащих тригонометрические функции, по отрезку длины Рассмотрим ещё один метод, где комплексные числа и вычеты используются вспомогательно при интегрировании действительных функций. Пусть дан интеграл При этом синус и косинус заменяются на
Надо ещё рассмотреть взаимосвязь дифференциалов. Если Пример. Вычислить интеграл Решение. Старый метод. Для сравнения, можно решить и старым методом, без комплексных чисел. Применим формулу понижения степени.
Новый метод.
Там, где полюс 3-го порядка, надо вычислить 2-ю производную от числителя, но 2 производная от константы равна 0. И только в 3-м слагаемом при вычислении вычета остаётся ненулевой результат, потому что там полюс 1 порядка, и производную от константы считать не нужно. Подставлять
Ответ.
ГЛАВА 2. РЯДЫ.
|
|||||
|
Последнее изменение этой страницы: 2020-11-22; просмотров: 249; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.72.224 (0.006 с.) |
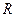 , при котором все эти особые точки включены в полукруг, и при дальнейшем увеличении радиуса полукруга, новые точки в нём уже не могут появиться.
, при котором все эти особые точки включены в полукруг, и при дальнейшем увеличении радиуса полукруга, новые точки в нём уже не могут появиться. на сумму вычетов во всех особых точках в верхнем полукруге. Граница состоит из двух частей:
на сумму вычетов во всех особых точках в верхнем полукруге. Граница состоит из двух частей:  и
и  , по отрезку
, по отрезку  движение влева направо, а по полуокружности
движение влева направо, а по полуокружности 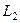 против часовой стрелки.
против часовой стрелки.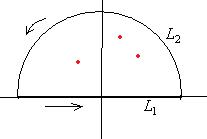
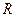 , при дальнейшем его увеличении, интеграл уже не будет меняться, потому что все особые точки верхней полуплоскости уже попали в полукруг, и других точек там нет. Если
, при дальнейшем его увеличении, интеграл уже не будет меняться, потому что все особые точки верхней полуплоскости уже попали в полукруг, и других точек там нет. Если 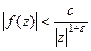 , то максимум модуля функции на полуокружности радиуса
, то максимум модуля функции на полуокружности радиуса  . А так как её длина равна
. А так как её длина равна 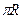 , т.е. интеграл
, т.е. интеграл 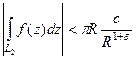 =
=  , эта величина стремится к 0 при
, эта величина стремится к 0 при 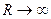 . Таким образом, при неограниченном увеличении радиуса, интеграл по дуге
. Таким образом, при неограниченном увеличении радиуса, интеграл по дуге  , то есть
, то есть 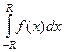 , который при
, который при 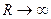 как раз и стремится к
как раз и стремится к 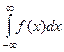 . То есть, в пределе интегральная теорема Коши применяется к верхней полуплоскости, а её граница - это действительная ось. Таким образом, мы вывели следующий факт:
. То есть, в пределе интегральная теорема Коши применяется к верхней полуплоскости, а её граница - это действительная ось. Таким образом, мы вывели следующий факт: аналитическая на действительной оси, а также в верхней полуплоскости, за исключением конечного числа особых точек, и при этом
аналитическая на действительной оси, а также в верхней полуплоскости, за исключением конечного числа особых точек, и при этом  , то
, то 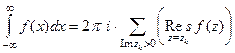 то есть несобственный интеграл по оси равен произведению
то есть несобственный интеграл по оси равен произведению 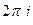 на сумму вычетов во всех особых точках верхней полуплоскости.
на сумму вычетов во всех особых точках верхней полуплоскости.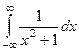 .
.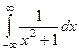 =
= 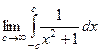 =
= 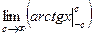 =
= 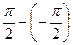 =
= 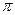 .
.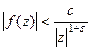 выполнено. Надо, чтобы разность степеней бала хотя бы чуть больше 1, а она равна 2.
выполнено. Надо, чтобы разность степеней бала хотя бы чуть больше 1, а она равна 2.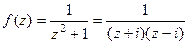 , которая на действительной оси как раз и совпадает с исходной функцией. Видно, что есть 2 полюса порядка 1, причём лишь один из них в верхней полуплоскости, а именно
, которая на действительной оси как раз и совпадает с исходной функцией. Видно, что есть 2 полюса порядка 1, причём лишь один из них в верхней полуплоскости, а именно 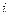 . Тогда
. Тогда =
= 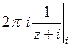 =
=  =
= 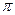 .
.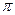 .
.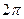 .
.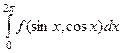 . При этом мы можем ввести замену
. При этом мы можем ввести замену 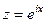 . Учитывая формулу Эйлера,
. Учитывая формулу Эйлера,  =
= 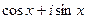 , то есть образы это точки с координатами
, то есть образы это точки с координатами  , т.е. отрезок длины
, т.е. отрезок длины  отображается на окружность единичного радиуса. А интеграл по окружности в комплексной плоскости можно вычислять с помощью интегральной теоремы Коши и вычетов.
отображается на окружность единичного радиуса. А интеграл по окружности в комплексной плоскости можно вычислять с помощью интегральной теоремы Коши и вычетов.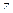 таким образом:
таким образом: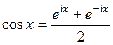 =
= 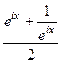 =
= 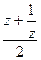
 =
=  =
= 

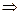
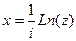
 =
= 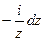 .
. .
. =
=  =
= 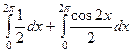 =
=  =
= =
= 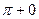 =
= 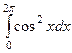 =
= 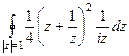 =
=  =
=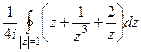 , разобьём на сумму 3 интегралов:
, разобьём на сумму 3 интегралов: . В первом, аналитическая функция, не имеющая особых точек. Интеграл от неё по замкнутому контуру равен 0. Во 2-м и 3-м слагаемом, единственным полюсом является точка
. В первом, аналитическая функция, не имеющая особых точек. Интеграл от неё по замкнутому контуру равен 0. Во 2-м и 3-м слагаемом, единственным полюсом является точка 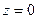 , но в одном из них полюс 3 порядка, а в другом 1 порядка.
, но в одном из них полюс 3 порядка, а в другом 1 порядка.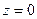 в функцию, тождественно равную 2, тоже нет необходимости, ведь она равна 2 в любой точке.
в функцию, тождественно равную 2, тоже нет необходимости, ведь она равна 2 в любой точке.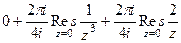 =
= 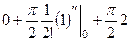 =
=  =
= 


