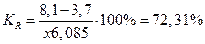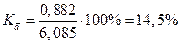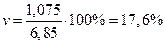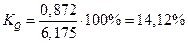Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Показатели центра распределенияСодержание книги
Поиск на нашем сайте
Для характеристики среднего значения признака в вариационном ряду используются средняя арифметическая, медиана и мода. Общие понятия о средних величинах были даны в главе 4. В данном параграфе рассмотрим расчет показателей центра распределения для вариационных рядов. Средняя арифметическая: Ø для дискретного ряда распределения: где
Ø для интервального ряда распределения: где
Для таблицы 1 средняя арифметическая равна:
Для таблицы 2 средняя арифметическая равна:
Медиана: Ø для дискретного ряда распределения положение медианы определяется ее номером Для примера в табл.1 Ø для интервального ряда распределения сразу можно определить интервал, в котором находится медиана. Затем определяем медиану по формуле:
h – величина интервала;
Для примера, приведенного в табл.2:
Мода: Ø для дискретного ряда распределения – наиболее часто встречающееся значение. Для табл.1 мода равна 4 (максимальная частота 8); Ø для интервального ряда распределения:
где
Для примера, приведенного в табл.2:
Показатели вариации Для измерения вариации используют абсолютные и относительные показатели. Абсолютные показатели: 1. Размах вариации (размах колебаний) – разность между максимальным и минимальным значениями признака в совокупности:
2. Среднее линейное отклонение: Ø Для несгруппированных данных: Ø Для сгруппированных данных (вариационного ряда):
3. Дисперсия Ø Для несгруппированных данных: Ø Для сгруппированных данных:
4. Среднее квадратическое отклонение равен квадратному корню из дисперсии, т.е.
5. Квартильное отклонение: Квартили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 25% единиц совокупности будут меньше по величине
Размах вариации, среднее линейное и средне квадратичное отклонение являются величинами именованными, они имеют те же единицы измерения, что и индивидуальные значения признака. Расчет показателей вариации для банков, сгруппированных по размеру прибыли, показан табл.3
Таблица 3
Для этой вариации:
При сравнении колеблемости различных признаков в одной и той же совокупности или же при сравнении одного и того же признака в нескольких совокупностях с различной величиной средней арифметической пользуются относительными показателями вариации: 1. Коэффициент осцилляции 2. Относительное линейное отклонение 3. Коэффициент вариации 4. Относительный показатель квартильной вариации
Для таблицы 2 относительные показатели вариации получились следующими:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-17; просмотров: 177; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.005 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

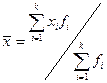 ,
,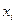 - варианты значений,
- варианты значений,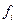 - частота повторения данного варианта
- частота повторения данного варианта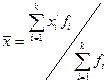 ,
,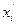 - середина соответствующего интервала.
- середина соответствующего интервала.
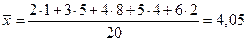 .
.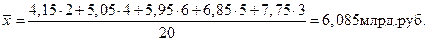
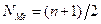 , где n – число единиц совокупности.
, где n – число единиц совокупности.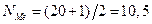 , т.е. медиана равна средней арифметической 10-го и 11-го значений признака. Ме=4.
, т.е. медиана равна средней арифметической 10-го и 11-го значений признака. Ме=4.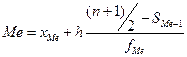 , где
, где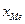 -нижняя граница медианного интервала;
-нижняя граница медианного интервала;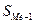 -накопленная частота интервала, предшествующая медианному;
-накопленная частота интервала, предшествующая медианному;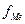 - частота медианного интервала.
- частота медианного интервала.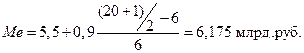
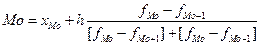 ,
,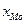 - начало модального признака;
- начало модального признака;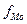 - частота, соответствующая модальному интервалу;
- частота, соответствующая модальному интервалу;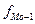 - предмодальная частота;
- предмодальная частота;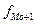 - послемодальная частота.
- послемодальная частота.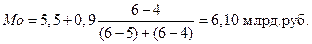
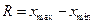 . Размах вариации зависит только от крайних значений признака, поэтому область его применения ограничена однородными совокупностями.
. Размах вариации зависит только от крайних значений признака, поэтому область его применения ограничена однородными совокупностями.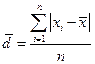 ;
;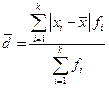 .
.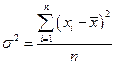 ;
;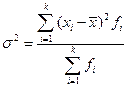 .
.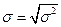 .
.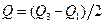 .
.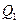 ; 25% будут заключены между
; 25% будут заключены между 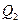 ; 25%- между
; 25%- между 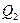 и
и 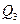 ; остальные 25% превосходят
; остальные 25% превосходят 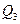 . Квартили определяются:
. Квартили определяются: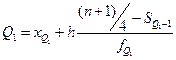 и
и 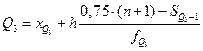 .
.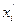
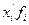
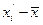
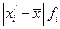
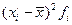
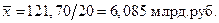 ;
;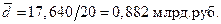 ;
; ;
;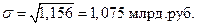
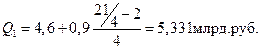 ;
;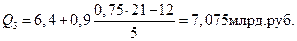
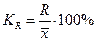 ;
;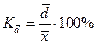 ;
;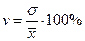 . Совокупность считается однородной, если коэффициент вариации не превышает 33%.
. Совокупность считается однородной, если коэффициент вариации не превышает 33%.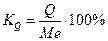 или
или 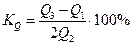 .
.