
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 3.6. Параллельные цепи синусоидального тока.Содержание книги Поиск на нашем сайте
Построение векторных диаграмм для разветвленных цепей.
ПРИМЕР. Напряжение на зажимах цепи с параллельным соединением резистора, конденсатора и катушки, активным сопротивлением которых можно пренебречь, U = 10 В. Параметры цепи: сопротивление резистора R = 500 Ом, емкость конденсатора С = 3,18 мкФ, индуктивность катушки L = 1,27 Гн при f = 50 Гц. Определить все токи и построить векторную диаграмму. Определить угол сдвига фаз.
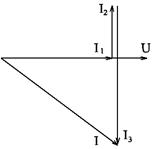
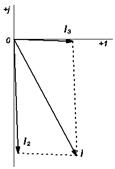
Рисунок 25. Решение. Ток резистора: Ток конденсатора: Ток катушки: Для определения общего тока цепи строим векторную диаграмму (рис. 26), выбрав масштабы MI = 0,005 А/см и МU = 2 В/см. Ток I1 имеет активный характер, поэтому он совпадает с напряжением по фазе. Ток I2 имеет емкостный характер, поэтому он опережает напряжение на угол 900. Ток I3 имеет индуктивный характер, поэтому он отстает от напряжения на угол 900. Из диаграммы видно, что общий ток
Рисунок 26.
Общий ток отстает от напряжения по фазе, следовательно характер цепи активно-индуктивный. Угол сдвига фаз:
Тема 3.7. Применение символического метода для расчёта цепей синусоидального тока. Расчёт цепей символическим методом. Задача 11.
Рисунок 26. Дано: Определить: Построить векторные диаграммы токов и напряжений:
ПРИМЕР.
Решение. Комплексы сопротивления участков:
Вектор напряжения цепи Тогда ток цепи где
Сопротивление цепи:
Тогда Напряжение на участках:
Токи на участках:
Полная (кажущаяся) мощность (комплекс) цепи
Векторные диаграммы токов и напряжений представлены на рис. 28.
Тема 4.1. Свободные колебания в контуре. Решение задач на определение характеристик колебательного контура. Задача 12. Определить индуктивность и емкость колебательного контура, если угловая частота собственных незатухающих колебаний ω0 = 104 с-1, характеристическое сопротивление контура ρ = 200 Ом. Чему равна добротность контура, если резистивное сопротивление R = 10 Ом? ПРИМЕР. В идеальном колебательном контуре с параметрами L = 10 мГн и С = 1 мкФ определить частоту свободных колебаний, период свободных колебаний и характеристическое сопротивление. Решение. Частоту свободных колебаний найдем по формуле:
Период определим, зная циклическую частоту свободных колебаний.
Характеристическое сопротивление контура:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 151; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.190.187 (0.006 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

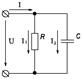 Рисунок 22.
Рисунок 22.
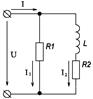 Рисунок 23.
Рисунок 23.
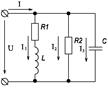 Рисунок 24.
Рисунок 24.
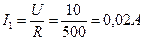 .
.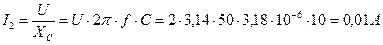 .
.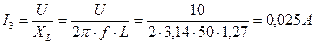 .
.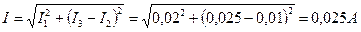 .
.
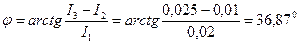 .
.
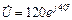 В.
В.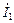 ,
, 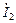 ,
,  ,
, 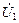 ,
, 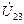 ,
, 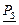 , Р, РQ,
, Р, РQ, 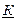 .
.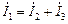 и
и 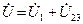 .
.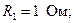
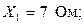
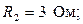
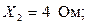
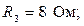
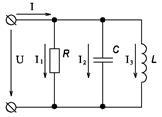
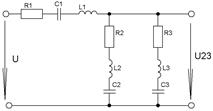
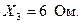 Определить токи всех участков, общий ток и мощность цепи, если
Определить токи всех участков, общий ток и мощность цепи, если 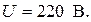
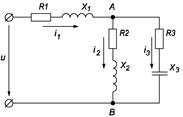 Рисунок 27.
Рисунок 27.
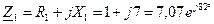 Ом;
Ом;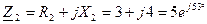 Ом;
Ом;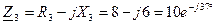 Ом.
Ом. направляем по мнимой оси, т.е.
направляем по мнимой оси, т.е. 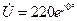 В.
В.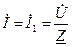 ,
,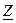 - комплекс сопротивления цепи, которое определяем следующим образом:
- комплекс сопротивления цепи, которое определяем следующим образом: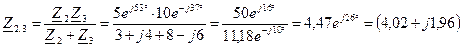 , Ом.
, Ом.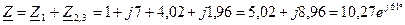 Ом.
Ом. А.
А.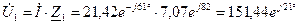 В;
В;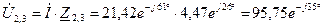 В.
В. А;
А;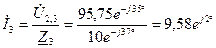 А.
А.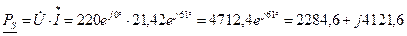
 .
.
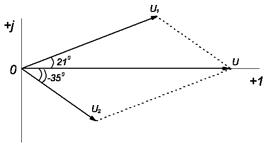
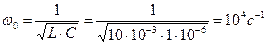 .
.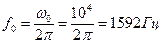 .
.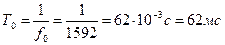 .
.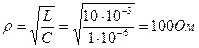 .
.


