
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1.1. Основы электростатики.Содержание книги Поиск на нашем сайте
Пояснения к их выполнению Тема 1.1. Основы электростатики. Расчёт цепей со смешанным соединением конденсаторов.
Пример.
Решение. Определяем, как соединены между собой конденсаторы на участках цепи, находим эквивалентные емкости участков и, постепенно упрощая схему, определяем эквивалентную емкость всей цепи. Конденсаторы С3 и С4 соединены последовательно (между ними нет узлов), их эквивалентная емкость:
Чертим (рис. 5) эквивалентную упрощенную схему, заменяя С3 и С4 конденсатором С34, и определяем по ней, что конденсаторы С2 и С34 соединен параллельно. Определяем эквивалентную емкость:
Чертим (рис. 6) эквивалентную укрощенную схему цепи, заменяя С2 и С34 эквивалентным С234. Конденсаторы С1 С234 и С5 соединены последовательно. Находим эквивалентную емкость всей цепи:
Определяем напряжения на конденсаторах, начиная с наиболее простой схемы (рис. 6). Найдем общий заряд:
По свойствам последовательного соединения конденсаторов:
Переходим к схеме (рис. 5) и, используя свойства параллельного соединения конденсаторов, получаем U2 = U34 = U234 = 36 В. Напряжения U3 и U4 определяем из схемы рис. 4, используя свойства последовательного соединения конденсаторов.
Определяем заряд и энергию:
Тема 1.2. Постоянный электрический ток. Решение задач на применение законов Ома. Задача 2.1 К аккумуляторной батарее с ЭДС Е = 12 В и внутренним сопротивлением Ri = 0,3 Ом подключен потребитель с сопротивлением R = 23,7 Ом. Определить ток, напряжение и падение напряжения на внутреннем сопротивлении источника. Задача 2.2 Потребитель энергии с сопротивлением R = 24 Ом подключен к источнику с ЭДС Е = 12,5 В и внутренним сопротивлением Ri = 1 Ом. Определить мощность источника, полезную мощность, потери мощности и коэффициент полезного действия.
Задача 2.3 Внутреннее сопротивление источника составляет 1,2 Ом. В согласованном режиме работы источника по цепи протекает ток I = 1,5 А. Определить напряжение источника при холостом ходе. Чему будет равен ток в режиме короткого замыкания? ПРИМЕР. К источнику электрической энергии с ЭДС = 30 В и внутренним сопротивлением Ri = 1 Ом подключен резистор R, сопротивление которого равно 2 Ом. Определить ток цепи I, напряжение на зажимах источника, мощность потребителя Р, мощность источника РИСТ и КПД цепи.
Решение. Силу тока найдем по закону Ома для замкнутой цепи:
Напряжение на зажимах цепи: Полезная мощность равна: Мощность источника: КПД цепи: Пример. Для электрической цепи, представленной на рисунке 10, определить токи в ветвях, мощность, развиваемую источником энергии и мощность потребителей. Проверить баланс мощности.
Решение. Поэтапно сворачивая схему, найдём общие сопротивление всех резисторов в цепи. Т.к. R5 и R6 соединены последовательно:
Резисторы R3 и R4 соединены параллельно, значит их общее сопротивление равно:
Резисторы R34 и R56 соединены параллельно:
Резисторы R2 и R3456 соединены последовательно:
Общее сопротивление равно:
Из схемы включения резисторов видно, что
По закону Ома найдём общий ток в цепи Iобщ.
Найдем токи, протекающие через резисторы R1 и R23456:
При последовательном соединении резисторов:
Найдём напряжение U3456:
При параллельном соединении резисторов:
Найдём токи протекающие через резисторы R3, R4 и R56:
Из схемы включения резисторов видно, что
Найдём мощность, развиваемую источником энергии и мощность потребителей:
Для проверки, правильно ли решена задача, найдём баланс мощностей по следующей формуле:
Задача решена верно. Задача 4.
- законов Кирхгофа; - наложения; - узлового напряжения; - ток в первой ветви метом эквивалентного генератора.
Рисунок 11.
ПРИМЕР.
Решение. Решение методом уравнений Кирхгофа.
Остальные m - (n - 1) = 2 уравнения составляем по второму закону Кирхгофа, например, для контура, состоящего из первой и второй ветвей и контура, состоящего из второй и третьей ветвей. Направление обхода каждого контура выбираем произвольно, например, по часовой стрелке. Записываем уравнения:
Получили систему уравнений:
Подставляя числовые значения сопротивлений и ЭДС, получаем:
Упрощая уравнения, получаем систему уравнений:
Для решения системы выразим значения I1 и I3 из второго и третьего уравнений:
Подставив эти значения в первое уравнение, определим ток I2.
Токи I 1 и I 3 определим из второго и третьего уравнений, подставив в них значение I2:
Знак «минус» перед значением I3 показывает, что действительное направление тока противоположно произвольно выбранному. Указываем действительное направление тока I3 штриховой стрелкой (см. рис. 13). Значения токов I1 и I2 получены со знаком «плюс», следовательно, их действительные направления совпадают с произвольно выбранными. Составляем баланс мощностей. Оба источника цепи являются генераторами, так как направления их ЭДС совпадают с направлениями токов тех ветвей, в которые они включены. Поэтому мощности источников Ри1 и Ри2 записываются со знаком «плюс»:
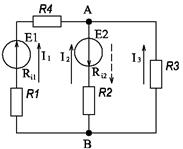
Решение методом узлового напряжения. Обозначаем узлы цепи через А и В инаправляем токи всех ветвей к одному узлу, например А(рис. 14).
Рисунок 14. Проводимость ветвей цепи:
Узловое напряжение:
В этой формуле значение Е1записывается со знаком «плюс», так как на правления I1 и Е1 совпадают, а E2 записывается со знаком «минус», так как направления I2 и Е2 противоположны.
Токи в ветвях:
Знак «минус» перед значением I2 показывает, что действительное направление I2 противоположно выбранному. Указываем штриховой стрелкой (рис. 14) действительное направление I2.
Решение методом наложения.
Выполняем расчет цепи (рис. 15), когда в ней действует один источник с Е1. Принимаем E2 = 0, а внутреннее сопротивление второго источника Ri2 оставляем в цепи. Сопротивления второй и третьей ветвей соединены параллельно между узлами А и В. Эквивалентное сопротивление участка АВ:
Эквивалентное сопротивление всей цепи:
Общий ток цепи: Напряжение на участке АВ: Токи: Выполняем расчет цепи (рис. 16), когда в ней действует один источник с Е2, принимаем е1 = 0, а внутреннее сопротивление первого источника Ri1 оставляем в цепи. Сопротивления первой и третьей ветвей соединены параллельно между узлами А и В. Эквивалентное сопротивление участка АВ:
Эквивалентное сопротивление всей цепи:
Общий ток цепи: Напряжение на участке АВ: Токи: Применяя метод наложения, определяем токи заданной цепи (см. рис. 14), созданные совместным действием источников. В первой ветви токи I'1 и I''1, (см. рис. 15 и 16) имеют одинаковое направление (к узлу А), поэтому Во второй ветви токи I'2 и I''2 (см. рис. 15 и 16) имеют одинаковое направление (к узлу В), поэтому В третьей ветви токи I'3 и I''3 (см. рис. 15 и 16) имеют противоположные направления, причем I''2 > I'2, поэтому
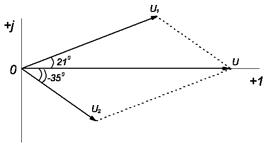
Задача 5. По временной диаграмме (рис. 17) определить: амплитуду, период, начальную фазу синусоидального тока. Рассчитать: частоту тока, угловую частоту, длину волны, действующее и среднее значение тока. Записать уравнение.
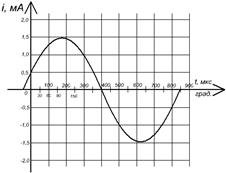
Рисунок 17. ПРИМЕР. По временной диаграмме (рис. 18) определить: амплитуду, период, начальную фазу синусоидального тока. Рассчитать: частоту тока, угловую частоту, длину волны, действующее и среднее значение тока. Записать уравнение.
Рисунок 18.
Решение. Амплитуда тока: Im = 1,5 мА; период тока: T = 900 мкс; начальная фаза тока: ψ = 300.
Частота тока: угловая частота: действующее значение тока: среднее значение тока: Уравнение переменного тока:
Задача 6. В цепи с резистором, подключенной к источнику с напряжением U = 200 В, протекает ток I = 10 мкА. Определить сопротивление и мощность резистора.
ПРИМЕР. Потребитель энергии с активным сопротивление R = 50 Ом подключен к источнику с напряжением u = 310,2sin(314t - 300) В. Определить действующие значения напряжения и тока, записать уравнение мгновенного значения тока, вычислить активную мощность цепи. Решение. Действующее значение напряжения: действующее значение тока: Амплитуда тока: В цепи с активным сопротивлением ток и напряжение совпадают по фазе, следовательно, начальные фазы у тока и напряжения одинаковы. Поэтому уравнение мгновенного значения тока Активная мощность цепи: Задача 7. Катушка с сопротивлениями R = 30 Ом и ХL = 100 Ом присоединена к источнику с напряжением U = 20,88 В. Определить угол сдвига фаз, активную, реактивную и полную мощность катушки. ПРИМЕР. Резистор сопротивлением R = 160 Ом соединен последовательно с катушкой с индуктивность L = 0,382 Гн. Напряжение на зажимах цепи U = 40 В, частота f = 50 Гц. Определить полное сопротивление цепи, ток, полное сопротивление катушки, напряжение резистора, напряжение катушки, активную мощность резистора, реактивную мощность катушки и полную мощность, угол сдвига фаз всей цепи и катушки. Построить векторную диаграмму. Решение. Индуктивное сопротивление катушки:
Полное сопротивление цепи:
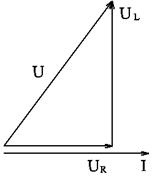
Ток в цепи: Напряжение резистора: напряжение катушки: Строим векторную диаграмму (рис. 19), выбрав масштабы МU = 0,6 В/cm, МI = 0,05 А/см.
Рисунок 19. Активная, реактивная, и полная мощности цепи:
Определяем угол сдвига фаз для всей цепи:
Тема 3.4. Цепь с ёмкостью. Решение задач на определение полного сопротивления цепи. Построение треугольника напряжений. Задача 8. Параметры цепи: R = 30 Ом и С = 15,9 мкФ. Напряжение на зажимах цепи U = 5 В при f = 250 Гц. Определить активную мощность цепи. Построить векторную диаграмму напряжений. ПРИМЕР. Резистор R = 60 Ом соединен последовательно с конденсатором С = 398 нФ. Напряжение на зажимах цепи U = 5 В при f = кГц. Определить ток, напряжения на резисторе и конденсаторе, угол сдвига фаз в цепи, активную, реактивную и полную мощности цепи. Построить векторную диаграмму. Решение. Емкостное сопротивление цепи:
Полное сопротивление цепи:
Ток: Напряжения на резисторе и конденсаторе, т. е. активная и емкостная составляющее напряжения:
Выбираем масштабы MI = 0,01 А/см и МU = 1 В/см в строим векторную диаграмму (рис. 20 ).
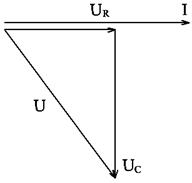
Рисунок 20. Угол сдвига фаз:
Активная, реактивная, и полная мощности цепи:
Задача 9. Параметры цепи U = 120 В, f = 100 Гц, I = 0,24 А. Определить активное сопротивление, угол сдвига фаз, напряжения на катушке и конденсаторе при L = 0,796 Гн, С = 7,95 мкФ. ПРИМЕР. Напряжение на зажимах цепи, представленной на рисунке 21, изменяется по закону u = Umsinωt. Частота питающего напряжения f = 50 Гц. Необходимо: 1. Определить показания приборов, указанных на схеме. 2. Определить закон изменения тока в цепи. 3. Определить закон изменения напряжения между точками, к которым подключен вольтметр. 4. Определить активную, реактивную и полную мощности источника, активную, реактивную, и полную мощности приемников. Составить и оценить баланс активной и реактивной мощностей.
Решение. 1) Закон изменения напряжения на зажимах цепи: u = Umsinωt, где ω = 2πf = 2·3,14·50 = 314 с-1. u = 260sin314t, В. Определим реактивные сопротивления цепи:
Общее активное и реактивное сопротивление при последовательном соединении найдем как:
Полное сопротивление цепи определим по формуле:
2) Чтобы определить показания амперметра, вольтметра и ваттметра, найдем действующие значения тока, напряжения на второй катушке индуктивности и активную мощность цепи. Максимальный ток в цепи равен:
Действующее значение тока равно:
Действующее значение напряжения на L2 и r2:
Активная мощность цепи:
3) Запишем закон изменения тока, зная что:
4) Закон изменения напряжения на L2:
Учитывая, что в цепи с индуктивностью напряжение опережает ток на 900, и
5) Найдем активные мощности приемников и источника.
Найдем реактивные мощности приемников и источника.
Найдем полные мощности приемников и источника.
Составим баланс активной и реактивной мощности. Для этого найдем мощность источника в комплексной форме (Р ИСТ = Р + jPQ) и сравним с мощностями, рассчитанными в пункте 6.
3132,9 Вт ≈ 3124 Вт Реактивная мощность источника РQИСТ: -893,4 ВАр ≈ -896 ВАр Полная мощность источника РSИСТ: 3257,8 ВА ≈ 3250 ВА Баланс мощностей сходится примерно, т.к. присутствует погрешность при округлении величин. ПРИМЕР. Напряжение на зажимах цепи с параллельным соединением резистора, конденсатора и катушки, активным сопротивлением которых можно пренебречь, U = 10 В. Параметры цепи: сопротивление резистора R = 500 Ом, емкость конденсатора С = 3,18 мкФ, индуктивность катушки L = 1,27 Гн при f = 50 Гц. Определить все токи и построить векторную диаграмму. Определить угол сдвига фаз.
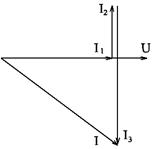
Рисунок 25. Решение. Ток резистора: Ток конденсатора: Ток катушки: Для определения общего тока цепи строим векторную диаграмму (рис. 26), выбрав масштабы MI = 0,005 А/см и МU = 2 В/см. Ток I1 имеет активный характер, поэтому он совпадает с напряжением по фазе. Ток I2 имеет емкостный характер, поэтому он опережает напряжение на угол 900. Ток I3 имеет индуктивный характер, поэтому он отстает от напряжения на угол 900. Из диаграммы видно, что общий ток
Рисунок 26.
Общий ток отстает от напряжения по фазе, следовательно характер цепи активно-индуктивный. Угол сдвига фаз:
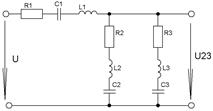
Задача 11.
Рисунок 26. Дано: Определить: Построить векторные диаграммы токов и напряжений:
ПРИМЕР.
Решение. Комплексы сопротивления участков:
Вектор напряжения цепи Тогда ток цепи где
Сопротивление цепи:
Тогда Напряжение на участках:
Токи на участках:
Полная (кажущаяся) мощность (комплекс) цепи
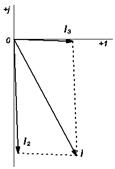
Векторные диаграммы токов и напряжений представлены на рис. 28.
Задача 12. Определить индуктивность и емкость колебательного контура, если угловая частота собственных незатухающих колебаний ω0 = 104 с-1, характеристическое сопротивление контура ρ = 200 Ом. Чему равна добротность контура, если резистивное сопротивление R = 10 Ом? ПРИМЕР. В идеальном колебательном контуре с параметрами L = 10 мГн и С = 1 мкФ определить частоту свободных колебаний, период свободных колебаний и характеристическое сопротивление. Решение. Частоту свободных колебаний найдем по формуле:
Период определим, зная циклическую частоту свободных колебаний.
Характеристическое сопротивление контура:
Задача 13. Последовательный колебательный контур, настроенный в резонанс на частоту f0 = 796 Гц, потребляет мощность P = 0,2 Вт при напряжении на зажимах контура U = 4 В. Добротность контура Q = 40. Определить параметры контура: ток, напряжение на катушке и конденсаторе, а также индуктивность и емкость. ПРИМЕР.
Решение. Резонансная угловая частота:
Резонансная циклическая частота:
Характеристическое сопротивление:
Добротность:
Затухание: Ток при резонансе: Расходуемая мощность: Напряжения на реактивных элементах:
Абсолютная полоса пропускания:
Задача 14. Определить резонансное сопротивление параллельного контура с параметрами L = 0,8 Гн, С = 5 мкФ, R = 5 Ом. Чему равна полоса пропускания и токи в ветвях при резонансе, если напряжение, приложенное к цепи U = 50 В? ПРИМЕР.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 287; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.236.101 (0.015 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

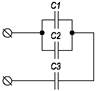 Рисунок 1.
Рисунок 1.
 Рисунок 2.
Рисунок 2.
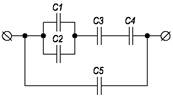 Рисунок 3.
Рисунок 3.
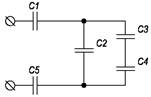 Рисунок 4.
Рисунок 4.
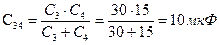 .
. .
.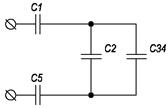 Рисунок 5.
Рисунок 5.
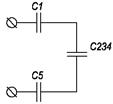 Рисунок 6.
Рисунок 6.
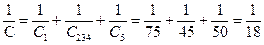 ;
; 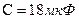 .
.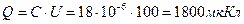 .
.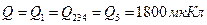 , тогда
, тогда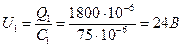 ;
;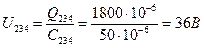 ;
;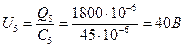 .
.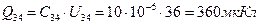 ,
,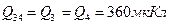 , тогда
, тогда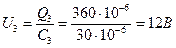 ;
;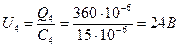 .
. ;
;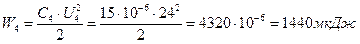 .
.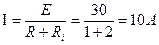 .
.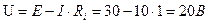 .
.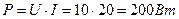 .
.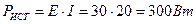 .
.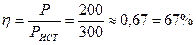 .
.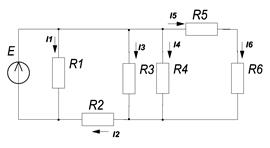 Рисунок 10.
Рисунок 10.
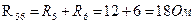 .
.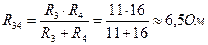 .
.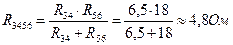 .
. .
.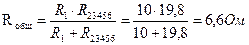 .
.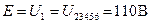 .
.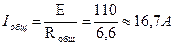
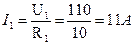 ;
;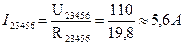 .
.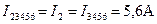 .
.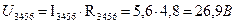 .
. .
.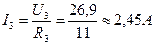 ;
;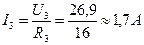 ;
;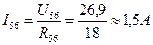 .
.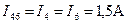 .
.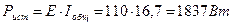 ;
;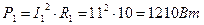 ;
;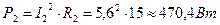 ;
;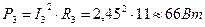 ;
;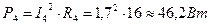 ;
;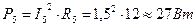 ;
;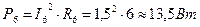 .
.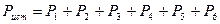
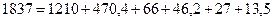
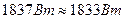

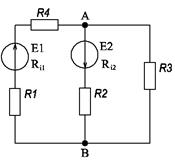 Рисунок 12.
Рисунок 12.
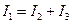 .
.
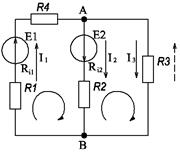 Рисунок 13.
Рисунок 13.
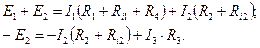
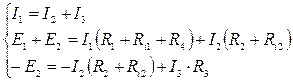
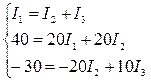
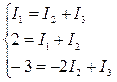
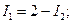
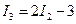 .
.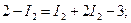
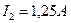 .
.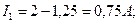
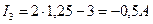 .
.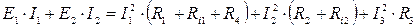
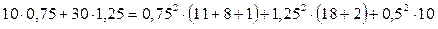
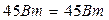 .
.
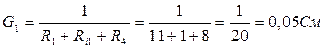 ;
;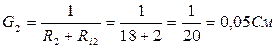 ;
;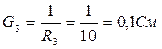 .
.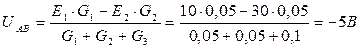 .
.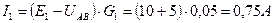 ;
;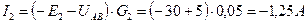 ;
;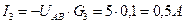 .
.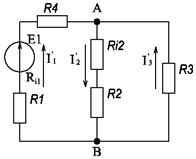 Рисунок 15.
Рисунок 15.
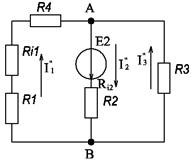 Рисунок 16.
Рисунок 16.
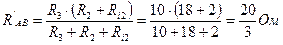 .
.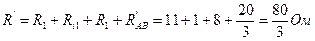 .
.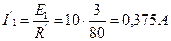 .
.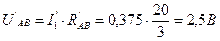 .
.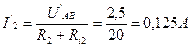 ;
; 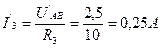 .
.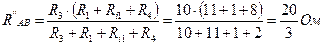 .
.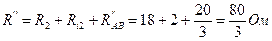 .
.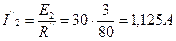 .
.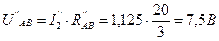 .
.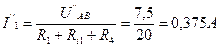 ;
; 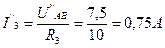 .
.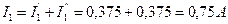 и направлен к узлу А.
и направлен к узлу А.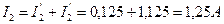 и направлен к узлу В.
и направлен к узлу В.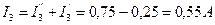 и направлен, как и ток I''3, к узлу А.
и направлен, как и ток I''3, к узлу А.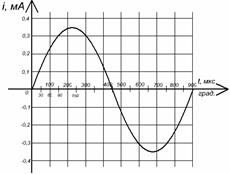
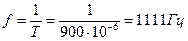 ;
;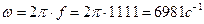 ;
;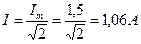 ;
;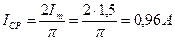 .
.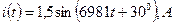 .
.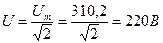 ;
;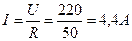 .
.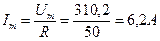 или
или 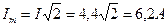 .
.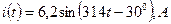 .
.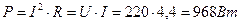 .
.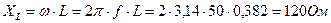 .
.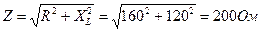 .
.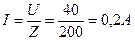 .
. 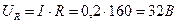 ,
,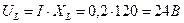 .
.
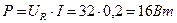 ;
; 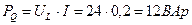 ;
; 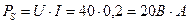 .
.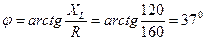 .
.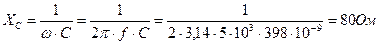 .
.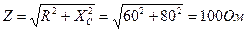 .
.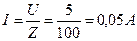 .
.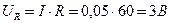 ;
; 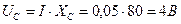 .
.
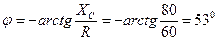 .
.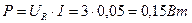 ;
; 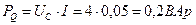 ;
; 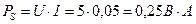 .
.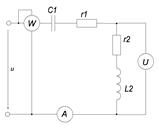 Рисунок 21.
Рисунок 21.
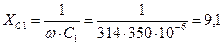 Ом
Ом Ом.
Ом.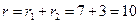 Ом;
Ом;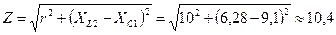 Ом.
Ом.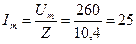 А.
А.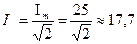 А.
А.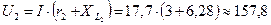 В.
В.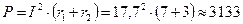 Вт.
Вт.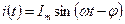 , где φ – угол сдвига фаз между напряжением и током в цепи.
, где φ – угол сдвига фаз между напряжением и током в цепи.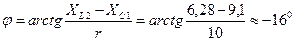 . Тогда
. Тогда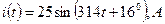 .
.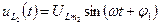 , где
, где 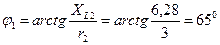 .
.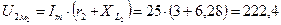 В получим:
В получим: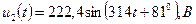 .
.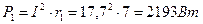
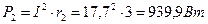
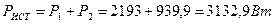
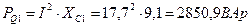
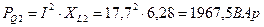
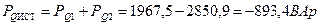
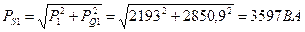
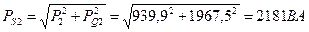
 Активная мощность источника РИСТ:
Активная мощность источника РИСТ: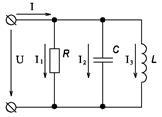
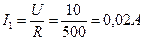 .
.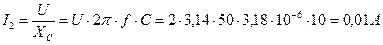 .
.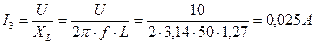 .
.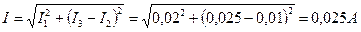 .
.
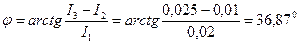 .
.
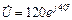 В.
В.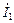 ,
, 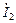 ,
,  ,
, 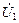 ,
, 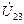 ,
, 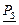 , Р, РQ,
, Р, РQ, 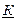 .
.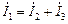 и
и 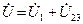 .
.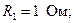
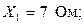
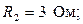
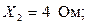
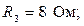
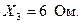 Определить токи всех участков, общий ток и мощность цепи, если
Определить токи всех участков, общий ток и мощность цепи, если 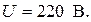
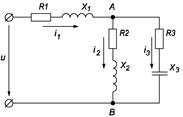 Рисунок 27.
Рисунок 27.
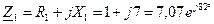 Ом;
Ом;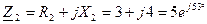 Ом;
Ом;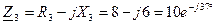 Ом.
Ом.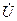 направляем по мнимой оси, т.е.
направляем по мнимой оси, т.е. 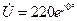 В.
В.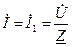 ,
,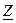 - комплекс сопротивления цепи, которое определяем следующим образом:
- комплекс сопротивления цепи, которое определяем следующим образом: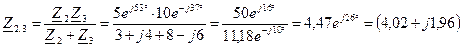 , Ом.
, Ом.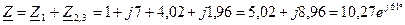 Ом.
Ом. А.
А.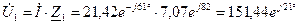 В;
В;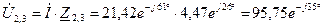 В.
В. А;
А;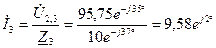 А.
А.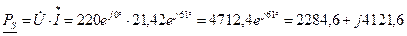
 .
.
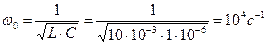 .
.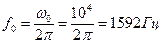 .
.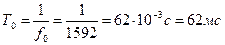 .
.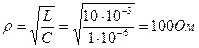 .
.
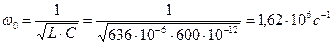 .
.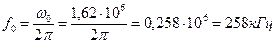 .
.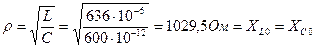
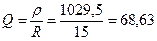 .
.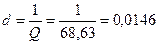 .
.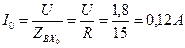 .
.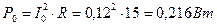 .
.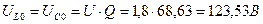 .
.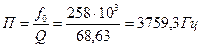 .
.


