Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предельные характеристики приема двоичных радиосигналовСодержание книги
Поиск на нашем сайте
При различении детерминированных сигналов (в детерминированном сигнале В задаче различения используется критерий идеального наблюдателя, минимизирующий вероятность полной ошибки. Минимум вероятности полной ошибки достигается при принятии решения по максимуму апостериорной вероятности. Вычислим полную вероятность ошибочного приема для случая, когда сигналы равновероятны и имеют одинаковую энергию.
Рис. 2.10. Оптимальные схемы для различения двух детерминированных сигналов с использованием: (а) согласованных фильтров; (б) корреляторов
Пусть присутствует первый сигнал, т. е.
описывается нормальной п. в.
где
условно называют коэффициентом взаимной корреляции между сигналами. Если присутствует сигнал
П.в. изображены
Вероятность полной ошибки определяется формулой
Значение порога h можно найти из условия минимума вероятности полной ошибки, т.е. из уравнения
где Ф(х) — интеграл вероятности. Следовательно, при известном отношении сигнал-шум 2E/N0 вычисление вероятности полной ошибки для детерминированных равновероятных сигналов с одинаковыми энергиями сводится к определению коэффициента взаимной корреляции между сигналами. Так как интеграл вероятности Ф(х) является монотонно возрастающей функцией аргумента, то при одинаковом отношении сигнал-шум наибольшей помехоустойчивостью (меньшей вероятностью ошибки ре) обладают сигналы, для которых коэффициент взаимной корреляции минимален. Коэффициент взаимной корреляции rs может изменяться от –1 (при s1= –s2) до +1 (при s1=s2). Ясно, что одинаковые сигналы (rs=1) невозможно различить и поэтому pe=1-Ф(0)=0,5. Наоборот, если сигналы одинаковы по форме и противоположны по знаку (rs = –1), то их различить легче, чем любые другие два сигнала (например, ортогональные с rs=0). Сказанное иллюстрирует рис. 2.12.
Рис. 2.12. Зависимость вероятности полной ошибки pe от коэффициента взаимной корреляции rs между детерминированными сигналами.
Кривые, характеризующие зависимость вероятности полной ошибки pe от отношения сигнал-шум при оптимальных методах приема детерминированных сигналов, в теории цифровых РСПИ принято называть кривыми потенциальной помехоустойчивости или предельными характеристиками приёма. Получим их для простейших двоичных радиосигналов с основными видами манипуляции. Фазовая манипуляция (ФМ). При фазовой манипуляции используются сигналы
Для таких сигналов rs = –1, поэтому получаем
Частотная манипуляция (ЧМ). При ЧМ используются сигналы
В данном случае при
Этот коэффициент минимален и равен
Амплитудная манипуляция (АМ). При АМ
В данном случае условие равенства энергий сигналов не выполняется, поэтому его следует рассмотреть отдельно. Система с АМ представляет собой систему с пассивной паузой. Приём сигналов в системах передачи информации с пассивной паузой обычно рассматривают в рамках задачи обнаружения с использованием критерия идеального наблюдателя. Выше был получен оптимальный алгоритм обнаружения
В отсутствие сигнала
есть результат линейного преобразования БГШ. Поэтому она при детерминированном сигнале
При наличии детерминированного сигнала
будет иметь также нормальную п.в. с параметрами
Плотности вероятности p0(q) и p1(q) изображены на рис. 2.13. Значение порога h также, как для ФМ и ЧМ, находим из условия минимума вероятности полной ошибки, т.е. из уравнения
Рис. 2.13. Нормальные плотности вероятности p0(q) и p1(q) в отсутствие и при наличии сигнала (pF – вероятность ложной тревоги, pD – вероятность правильного обнаружения)
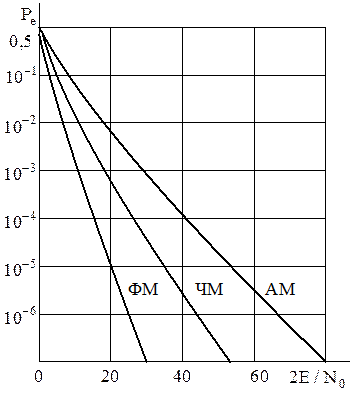
Графики полученных трёх зависимостей приведены на рис. 2.14.
Рис. 2.14. Зависимость вероятности ошибки от отношения сигнал-шум для детерминированных радиосигналов при ФМ, ЧМ и АМ.
Сравнивая представленные графики для ФМ, ЧМ и АМ, видим, что при одной и той же энергии элементарных сигналов (а не средней энергии) из трех рассмотренных видов манипуляции наибольшей помехоустойчивостью обладает фазовая манипуляция и наименьшей — амплитудная.
Выводы по оптимальному приёму двоичных сигналов в системах передачи дискретных сообщений: 1. В общем случае оптимальный приёмник двоичных радиосигналов представляет собой двухканальную систему. В каждом из каналов размещается коррелятор или фильтр, согласованный с одним из двух возможных сигналов. 2. Предположение о детерминированности сигналов (все параметры сигналов априорно известны, неизвестно только то, какой из двух возможных сигналов был передан) позволяет получить предельные (потенциальные) характеристики приёма. Наивысшей потенциальной помехоустойчивостью среди двоичных радиосигналов обладают сигналы с манипуляцией фазы на 180 градусов (противоположные ФМ сигналы).
|
||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 141; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.31.48 (0.01 с.) |

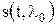 значение параметра l априорно точно известно и равно l0, т.е.
значение параметра l априорно точно известно и равно l0, т.е. 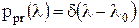 ) достигаются предельные (потенциальные) возможности (верхние границы) для характеристик различения.
) достигаются предельные (потенциальные) возможности (верхние границы) для характеристик различения.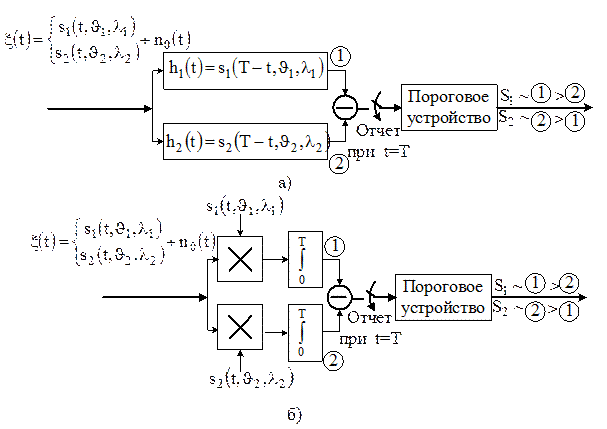
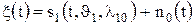 . Тогда сл. в.
. Тогда сл. в.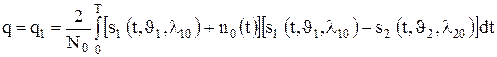
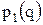 со следующими характеристиками:
со следующими характеристиками: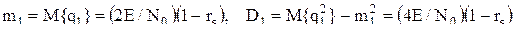 ,
,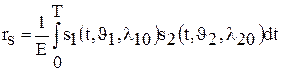
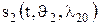 , то сл. в. q = q2 имеет нормальную п.в.
, то сл. в. q = q2 имеет нормальную п.в. 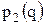 с характеристиками
с характеристиками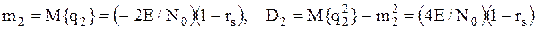 .
. на рис. 2.11.
на рис. 2.11.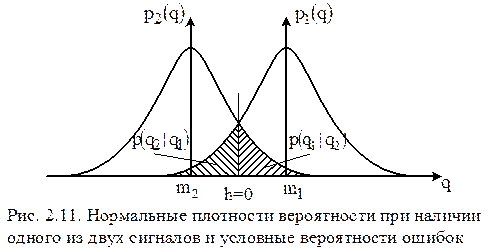
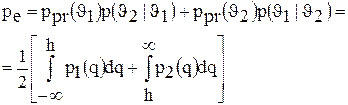
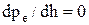 . Для априорно равновероятных сигналов это уравнение сводится к
. Для априорно равновероятных сигналов это уравнение сводится к 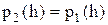 , что выполняется при h=0. Выполнив вычисления, получим
, что выполняется при h=0. Выполнив вычисления, получим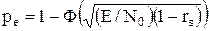 ,
,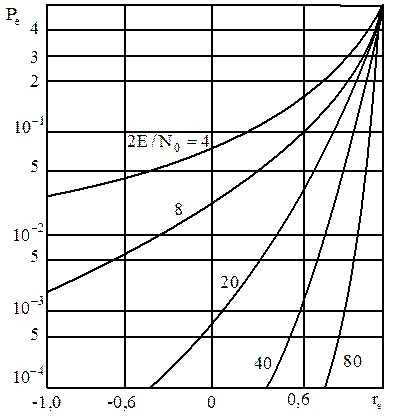
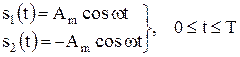 .
.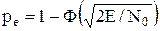 .
.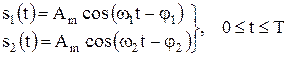 .
.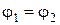 имеем
имеем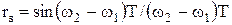 .
.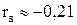 при
при 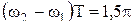 . Однако на практике обычно выполняется неравенство
. Однако на практике обычно выполняется неравенство 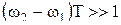 . Поэтому
. Поэтому 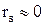 (применяются ортогональные ЧМ сигналы) и тогда получим
(применяются ортогональные ЧМ сигналы) и тогда получим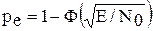 .
.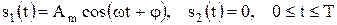 .
.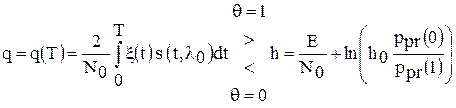 .
.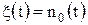 и сл.в.
и сл.в.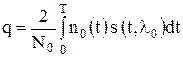
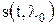 будет иметь нормальную п.в. с м.о. и дисперсией
будет иметь нормальную п.в. с м.о. и дисперсией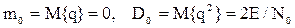 .
.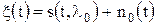 и сл.в.
и сл.в.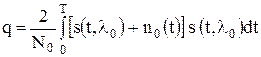
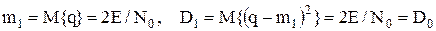 .
.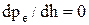 . Для априорно равновероятных сигналов это уравнение сводится к
. Для априорно равновероятных сигналов это уравнение сводится к 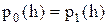 , что выполняется при h=
, что выполняется при h= 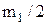 . Отсюда получаем
. Отсюда получаем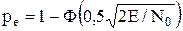 .
.