
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные положения теории статистических решений
Фундаментальную роль в современной теории статистических решений и теории оптимального приема радиосигналов играет формула Байеса (теорема гипотез). С её помощью можно, приняв колебание Формула Байеса является решением следующей задачи проверки гипотез (рис. 2.1). Пусть события А,В,С могут произойти только при появлении одного из несовместных событий (гипотез) H1, H2,...Hn. Предполагается, что известны априорные вероятности гипотез Р(H1), Р(H2),...,Р(Hn) и условные вероятности перехода Р(А|Hi), i=1,2,…,n – вероятности события А при условии, что справедлива гипотеза Hi.
Рис. 2.1. Задача проверки гипотез
Допустим, что произведено испытание (выполнен эксперимент), в результате которого появилось событие А. Необходимо определить, с какой из гипотез следует связывать появление события А, т.е. определить, следствием какой гипотезы явилось это событие. Иначе говоря, требуется определить апостериорные (послеопытные) вероятности гипотез Р(H1|A), Р(H2|A),…,Р(Hn|A) при условии, что в результате опыта произошло событие A. Апостериорная вероятность гипотезы Р(Hi|A) равна отношению вероятности Р(Hi,A) совместного появления событий Hi и А к полной (средней) вероятности Р(А) события А:
Это и есть формула Байеса. Вывод формулы Байеса основан на использовании теоремы умножения вероятностей и формулы полной (средней) вероятности. В данном случае события Hi и А совместны и зависимы. Поэтому по теореме умножения вероятностей P(A,Hi)= P(A)P(Hi|A)= P(Hi)P(A|Hi). В соответствии с формулой полной (средней) вероятности
Поясним смысл составляющих, входящих в формулу Байеса, предварительно записав её в несколько ином виде
где Таким образом, правая часть формулы Байеса состоит из трёх сомножителей: 1 – константа, 2 - априорная вероятность P(Hi), характеризующая неопределенность гипотезы Hi до опыта, 3 – условная вероятность P(А|Hi) события А в предположении, что верна гипотеза Hi, её иногда называют функцией правдоподобия. Вероятность P(А|Hi) уточняет априорную вероятность на основе результатов эксперимента. Апостериорная вероятность P(Hi|А) гипотезы Hi характеризует пересмотренное значение априорной вероятности P(Hi) после получения дополнительной информации о появлении события А. Формула Байеса позволяет определить вероятности гипотез после того, как появилось событие А (или В, или С). Необходимость в проведении эксперимента возникает тогда, когда априорные вероятности кажутся недостаточно надежными и требуют уточнения. Из формулы видно, что при определении апостериорной вероятности P(Hi|А) нужно учитывать как первоначальные (априорные) данные о гипотезах, характеризуемых вероятностью P(Hi), так и результаты опыта (произошло событие А, а не какое-либо другое). Методика решения задач с применением формулы Байеса такова. Пусть в результате опыта (эксперимента) произошло событие А. В РСПИ под опытом понимается передача сообщения по каналу связи, тогда можем считать, что на выходе канала зарегистрировано событие А (это событие может состоять в том, что колебание Рассмотрим байесовский подход к статистическому оцениванию («философию» байесовского подхода). При таком подходе интересующий нас параметр (сообщение) рассматривается как реализованное значение сл. в.
Введение априорного распределения влечет за собой два последствия. Во-первых, функция Во-вторых, тот факт, что Отметим, что при таком подходе вероятность численно выражает «степень нашей разумной уверенности» в справедливости некоторого утверждения, и, следовательно, вероятность здесь выходит за рамки ее статистической интерпретации и может трактоваться как некая «субъективная вероятность». Польза от введения априорной п. в., с одной стороны, состоит в том, что это дает способ присоединения необходимой для анализа информации, а с другой - это выигрыш с точки зрения логической ясности. Теорема гипотез, которая комбинирует априорное распределение и опытные данные так, чтобы получить апостериорное распределение, впервые была сформулирована Томасом Байесом в 1763 г. Подход к теории статистического вывода, основанный на систематическом использовании этой теоремы, также носит имя Байеса. Общая логическая схема байесовского метода оценивания неизвестных значений параметров представлена на рис. 2.2.
Рис. 2.2. Схема байесовского оценивания параметров
Рассмотрим реализацию схемы байесовского оценивания неизвестного параметра. Априорные сведения о параметре l основаны на предыстории функционирования анализируемого процесса (если такая имеется) и на профессиональных теоретических соображениях о его сущности, специфике, особенностях и т.п. В результате эти априорные сведения должны быть представлены в виде функции
Опытные (статистические) данные
где Хотя по форме функция правдоподобия Вычисление апостериорного распределения
Здесь Таким образом, получаем вид формулы Байеса в виде произведения трёх сомножителей
Построение байесовских оценок основано на использовании знания апостериорного распределения
|
|||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 154; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.116.20 (0.012 с.) |
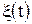 , вычислить апостериорные (послеопытные) плотности вероятности (для непрерывного сообщения) или вероятности (для дискретного сообщения) всех значений сообщения (гипотез), которые в действительности могли быть переданы и за оценку принять, например, то значение, апостериорная плотность вероятности или вероятность которого максимальна. При этом решении не исключены ошибки. Однако они будут минимальными по сравнению с другими решениями. Чтобы иметь надежные результаты для принятия решения иногда проводятся последовательные эксперименты. В таком случае апостериорные плотности вероятности или вероятности гипотез после первого эксперимента принимаются в качестве априорных (доопытных) для второго эксперимента и т.д.
, вычислить апостериорные (послеопытные) плотности вероятности (для непрерывного сообщения) или вероятности (для дискретного сообщения) всех значений сообщения (гипотез), которые в действительности могли быть переданы и за оценку принять, например, то значение, апостериорная плотность вероятности или вероятность которого максимальна. При этом решении не исключены ошибки. Однако они будут минимальными по сравнению с другими решениями. Чтобы иметь надежные результаты для принятия решения иногда проводятся последовательные эксперименты. В таком случае апостериорные плотности вероятности или вероятности гипотез после первого эксперимента принимаются в качестве априорных (доопытных) для второго эксперимента и т.д.


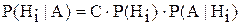 ,
, - константа, имеющая одно и то же постоянное значение для возможных гипотез H1, H2,...Hn.
- константа, имеющая одно и то же постоянное значение для возможных гипотез H1, H2,...Hn.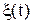 приняло некоторое вполне определённое значение). Необходимо, во-первых, вычислить вероятности гипотез при условии, что произошло событие А, т.е. вычислить апостериорные вероятности P(Hi|А), i=1,2,…,n. Во-вторых, сравнить полученные вероятности между собой. В-третьих, принять решение, т.е., например, отдать предпочтение той гипотезе, которая имеет наибольшую апостериорную вероятность.
приняло некоторое вполне определённое значение). Необходимо, во-первых, вычислить вероятности гипотез при условии, что произошло событие А, т.е. вычислить апостериорные вероятности P(Hi|А), i=1,2,…,n. Во-вторых, сравнить полученные вероятности между собой. В-третьих, принять решение, т.е., например, отдать предпочтение той гипотезе, которая имеет наибольшую апостериорную вероятность. с распределением
с распределением  , называемым априорным распределением параметра
, называемым априорным распределением параметра  содержит информацию о параметре
содержит информацию о параметре  , так как описывает степень уверенности в том, что этот параметр примет то или иное значение, еще до начала сбора опытных (статистических) данных. И если эта информация верна, выводы о параметре
, так как описывает степень уверенности в том, что этот параметр примет то или иное значение, еще до начала сбора опытных (статистических) данных. И если эта информация верна, выводы о параметре 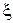 , заключена в условном распределении
, заключена в условном распределении 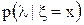 , называемом апостериорным (х – реализованное значение сл. в.
, называемом апостериорным (х – реализованное значение сл. в.  ). Таким образом, по мере поступления опытных (статистических) данных приёмник уточняет (пересчитывает) распределение, переходя от априорного распределения к апостериорному.
). Таким образом, по мере поступления опытных (статистических) данных приёмник уточняет (пересчитывает) распределение, переходя от априорного распределения к апостериорному.
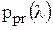 , задающей априорное распределение параметра и интерпретируемой как вероятность того, что параметр примет значение, равное λ, если параметр по своей природе дискретен, и как плотность вероятности в точке λ, если параметр непрерывен. Заметим лишь, что в ситуациях, когда априорных сведений об анализируемом параметре слишком мало, в качестве априорного распределения
, задающей априорное распределение параметра и интерпретируемой как вероятность того, что параметр примет значение, равное λ, если параметр по своей природе дискретен, и как плотность вероятности в точке λ, если параметр непрерывен. Заметим лишь, что в ситуациях, когда априорных сведений об анализируемом параметре слишком мало, в качестве априорного распределения  используют, например, равномерное на отрезке
используют, например, равномерное на отрезке  распределение, где
распределение, где  — априорный диапазон варьирования возможных значений оцениваемого параметра, т. е.:
— априорный диапазон варьирования возможных значений оцениваемого параметра, т. е.: .
.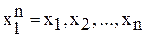 — это не что иное, как выборка объема n из анализируемой генеральной совокупности: для РСПИ это, как правило, n значений (выборок, отсчётов) принимаемого колебания
— это не что иное, как выборка объема n из анализируемой генеральной совокупности: для РСПИ это, как правило, n значений (выборок, отсчётов) принимаемого колебания 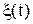 . Получая опытные (статистические) данные, мы к имевшейся ранее априорной информации о параметре присоединяем выборочную (эмпирическую, опытную) информацию. Вычисление функции правдоподобия
. Получая опытные (статистические) данные, мы к имевшейся ранее априорной информации о параметре присоединяем выборочную (эмпирическую, опытную) информацию. Вычисление функции правдоподобия 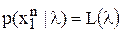 производится при независимых выборках
производится при независимых выборках  по формуле
по формуле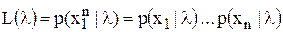 ,
, — значение плотности вероятности сл.в.
— значение плотности вероятности сл.в.  , при условии, что значение оцениваемого параметра равно
, при условии, что значение оцениваемого параметра равно  совпадает с условной плотностью вероятности
совпадает с условной плотностью вероятности  , описывающей закон распределения вероятностей анализируемой генеральной совокупности - мы пишем
, описывающей закон распределения вероятностей анализируемой генеральной совокупности - мы пишем  является параметр
является параметр  заданы – это значения входного колебания
заданы – это значения входного колебания 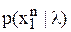 подставляются те значения
подставляются те значения 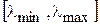 . Следовательно, функция правдоподобия позволяет определить то значение
. Следовательно, функция правдоподобия позволяет определить то значение 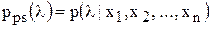 осуществляется с помощью формулы Байеса. В результате имеем следующий вариант формулы Байеса
осуществляется с помощью формулы Байеса. В результате имеем следующий вариант формулы Байеса .
.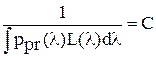 - константа, находимая из условия нормировки плотности вероятности и поэтому называемая нормировочной константой.
- константа, находимая из условия нормировки плотности вероятности и поэтому называемая нормировочной константой. .
.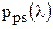 .
.


