
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерии оптимального приема радиосигналов
Как было отмечено выше, наиболее общей задачей оптимального приёма радиосигналов в РСПИ является задача фильтрации. Задача фильтрации по существу есть задача оценивания случайного процесса. Задача оценки параметров является частным случаем задачи фильтрации, когда фильтруемый параметр за время наблюдения не успевает заметно измениться. Оценивание параметров (значений непрерывных случайных величин) характерно для радиосистем передачи непрерывных сообщений. При байесовском подходе к оцениванию параметров радиосигналов критерий оптимальности связывают с функцией потерь
Выражение в квадратных скобках, зависящее от правила оценки
Оптимальной байесовской оценкой – оценкой оптимальной по критерию минимума среднего риска – называют оценку, найденную из уравнения Интеграл
Итак, байесовские оптимальные правила оценки можно найти, оперируя апостериорным риском, который определяется апостериорным распределением сообщения На практике во многих случаях используют функции потерь, зависящие только от ошибки оценки
Можно показать, что, например, квадратичной функции потерь соответствует апостериорное среднее, т.е. байесовская оценка при квадратичной функции потерь является оптимальной по критерию минимума среднего квадрата ошибки и представляет собой м.о. апостериорной п.в.
простой функции потерь – оценка оптимальная по критерию максимума апостериорной плотности вероятности
а модульной функции потерь – медиана апостериорной плотности вероятности. Отметим, что при симметричной унимодальной функции апостериорной п.в. все три оценки совпадают.
Теперь рассмотрим критерии решения задач оптимального приёма радиосигналов в радиосистемах передачи дискретных сообщений – задач различения сигналов и обнаружения сигнала. Решение этих задач основано на решении простейшей задачи статистической теории решений - задачи статистической проверки двух гипотез. Рис. 2.3. иллюстрирует компоненты этой задачи.
Рис. 2.3. Задача статистической проверки двух гипотез
Первым элементом является источник сообщений или гипотез, которые в простейшем случае представляют собой результат выбора из двух возможных значений. В случае двух возможных гипотез обозначим их, например, через Н1 и H2. Например, в цифровой системе связи передача информации осуществляется посылкой единиц и нулей. Посылке «единицы» соответствует H1, а посылке «нуля» — Н0. Мы не знаем, какая именно гипотеза является истинной. Вторым элементом задачи является вероятностный механизм перехода и третьим — пространство наблюдений. Механизм перехода можно рассматривать как некое устройство, которое знает, какая гипотеза является истинной. Основываясь на этом знании, оно генерирует некоторую точку в пространстве наблюдений в соответствии с некоторым вероятностным законом. Четвертым элементом задачи является правило решения. После наблюдения исхода в пространстве наблюдений мы пытаемся установить, какая гипотеза была истинной, и для выполнения этой процедуры вводим правило решения, согласно которому каждая точка относится к одной из гипотез. Предполагается, что пространство наблюдений соответствует ряду из N результатов наблюдений: r1, r2,…, rN. Поэтому каждый ряд можно себе представить как точку в N-мерном пространстве и обозначить вектором r: Вероятностный механизм перехода генерирует точки в пространстве наблюдений в соответствии с двумя известными условными плотностями вероятностей
В задаче проверки двух гипотез нам известно, что верна либо гипотеза H0, либо гипотеза H1. Итак, при каждом испытании возможен один из четырех исходов: 1) верна H0, выбираем H0; 2) верна H0, выбираем H1; 3) верна H1, выбираем H1, 4) верна H1, выбираем H0. Ясно, что первый и третий исходы соответствуют правильным выборам, а второй и четвертый - ошибочным. Смысл критерия решения состоит в том, что каждому из четырех возможных исходов (образов действия) придается некоторое относительное значение. Естественно предположить, что метод обработки принимаемой информации будет зависеть от выбранного нами критерия решения. Критерий Байеса. Байесовское испытание основывается на двух допущениях. Оба значения выходной величины источника подчиняются некоторым распределениям вероятностей, которые обозначим соответственно через P0 и Р1 и назовем априорными вероятностями. Эти вероятности отображают информацию, которой располагает наблюдатель до проведения эксперимента. Каждому из возможных образов действия приписывается некоторая стоимость (потери, риск). Обозначим стоимости четырех упомянутых образов действия через С00 ,С01, С10 и С11 соответственно. Первая цифра подстрочного индекса означает выбранную гипотезу, а вторая — гипотезу, которая была правильной. Поскольку каждый опыт сопряжен с определенными потерями, желательно, чтобы наше правило решения было построено таким образом, чтобы в среднем эти потери были как можно меньше. Для этого запишем сначала выражение для ожидаемой величины потерь. Имеются две вероятности, по которым мы должны усреднить: априорная вероятность и вероятность того, что будет предпринят заданный образ действий. Обозначая ожидаемую величину потерь как риск Â, имеем
Поскольку мы предположили, что по правилу решения следует выбирать либо H1, либо H0, его можно рассматривать, как правило разбиения пространства наблюдений Z на две части: Z1 и Z0 (рис.2.4).
Рис. 2.4. Разбиение пространства наблюдений на две части
Таким образом, если результат наблюдения оказывается в Z1, то принимается H1, а если в Z0 — то H0. Теперь можно написать выражение для риска через переходные вероятности и подпространства решений:
Для n-мерного пространства наблюдений интегралы являются n-кратными. Положим, что стоимость ошибочно принятого решения выше, чем стоимость правильного решения, т.е., C10>C00, C01>C11. Теперь для нахождения результата байесовского испытания нам необходимо выбрать подпространства решений Z1 и Z0 так, чтобы величина риска была сведена к минимуму. Требование обязательного принятия решения означает, что каждая точка R пространства наблюдений Z должна быть поставлена в соответствие подпространству Z1 или Z0. Таким образом, Z=Z0+Z1. Тогда получим
Учитывая условия нормировки можно прийти к
Отметим, что первые два члена соответствуют фиксированной стоимости, а интеграл представляет собой стоимость, определяемую теми точками R, которые относятся к Z0. Из допущения C10>C00, C01>C11 следует, что разности, заключенные в круглых скобках, являются положительными. Поэтому все значения R, когда второй член больше, чем первый, следует включить в Z0, так как ими вносится в интеграл отрицательная величина. Аналогично, все значения R, когда второй член больше первого, следует исключить из Z0 (отнести к Z1), поскольку ими вносится в интеграл положительная величина. Значения R, соответствующие равенству двух членов, на стоимость не влияют, и поэтому их можно распределять произвольно. Допустим, что эти точки относятся к H1, и не будем учитывать их в наших последующих рассуждениях. Таким образом, области решений определяются следующим условием: если
то относим R к Z1 и, следовательно, утверждаем, что истинна H1; в противном случае приписываем R к Z0 и утверждаем, что истинна H0. Последнюю формулу можно записать в виде
Отношение функций в левой части неравенства называют отношением правдоподобия и обозначают через
Так как оно представляет собой отношение двух функций сл. в., то и само является случайной величиной. При этом ясно, что независимо от размерности R величина
Таким образом, критерий Байеса приводит нас к критерию отношения правдоподобия
Процедура обработки данных, таким образом, сводится к вычислению Так как натуральный логарифм — функция монотонная, а обе части неравенства — величины положительные, то эквивалентной формой записи критерия отношения правдоподобия будет
Схема устройства обработки, реализующего процедуру проверки, изображена на рис. 2.5.
Рис. 2.5. Схема устройства обработки, реализующего критерий отношения правдоподобия
Существует несколько специальных видов критериев Байеса, которые часто используются и поэтому заслуживают отдельного рассмотрения. Критерий идеального наблюдателя. Если принять С00=С11=0, a С01=С10=1, то выражение для риска приводится к виду
Нетрудно усмотреть, что это выражение дает полную вероятность допустить ошибку. Следовательно, для данного распределения стоимости критерий Байеса минимизирует полную вероятность ошибки. При этом критерий можно записать в виде
Это решающее правило по критерию идеального наблюдателя эквивалентно принятию решения по критерию максимума апостериорной вероятности. Соответствующие устройства обработки называются приемниками с минимальной полной вероятностью ошибки.
Если две гипотезы априорно равновероятны, порог равен нулю. Это допущение обычно справедливо применительно к цифровым системам связи. Минимаксный критерий. Другой частный случай соответствует ситуации, когда априорные вероятности неизвестны. Для исследования этого случая обратимся к условным вероятностям ошибок.
Вероятность Обозначая С01=СМ, С10=СF, напишем выражение для риска
Представим себе, что априорные вероятности выбираются с таким расчетом, чтобы риск был максимальным. Если теперь поставить цель: минимизировать этот максимально возможный риск (соответствующий этому подходу критерий называется минимаксным критерием), то мы придем к минимаксному уравнению CMPM=CFPF. Критерий Неймана — Пирсона. Во многих физических ситуациях бывает затруднительно предсказать достаточно реалистичные стоимости и априорные вероятности. Эту трудность можно довольно просто обойти, если иметь дело с условными вероятностями PF и PD. Вообще говоря, нам хотелось бы сделать PF как можно меньше, а PD как можно больше. В большинстве задач, имеющих практическое значение, эти цели являются противоречащими друг другу. Критерий Неймана-Пирсона применяется в задаче обнаружения, в которой Очевидный критерий заключается в том, чтобы ограничить одну из вероятностей и максимизировать (или минимизировать) другую. Точная формулировка этого критерия приводится ниже. Ограничим или Очевидно, что при
Теперь ясно, что при любом положительном значении l критерий отношения правдоподобия минимизирует функцию F, так как для минимизации F мы относим точку R к области Zо только тогда, когда член в квадратных скобках отрицателен. Это эквивалентно критерию
Таким образом, функция F минимизируется по критерию отношения правдоподобия. Для того чтобы удовлетворить указанному ограничению, выберем l такое, что Решая это уравнение относительно l, получим величину порога. Итак, оптимальный обнаружитель Неймана-Пирсона должен формировать отношение правдоподобия и сравнивать его с порогом. Таким образом, этот обнаружитель полностью совпадает с оптимальным байесовским алгоритмом. Отличие состоит лишь в значении порога.
|
||||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 207; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.67.166 (0.048 с.) |
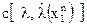 , придающей разный вес различным отклонениям оценки
, придающей разный вес различным отклонениям оценки 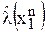 от истинного значения параметра λ. Конкретное значение функции потерь
от истинного значения параметра λ. Конкретное значение функции потерь  случайно, т.к. зависит от наблюдения
случайно, т.к. зависит от наблюдения 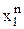 , и поэтому качество оценки характеризуют средними потерями - средним риском:
, и поэтому качество оценки характеризуют средними потерями - средним риском: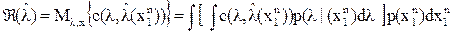 .
.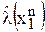 и от наблюдения
и от наблюдения 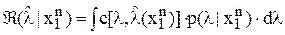 .
.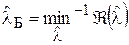 .
.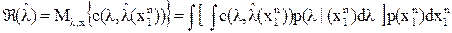 минимизируется, если при каждом значении наблюдения
минимизируется, если при каждом значении наблюдения 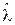 произведение
произведение  . Поскольку можно считать
. Поскольку можно считать  при каждом практически возможном значении наблюдения
при каждом практически возможном значении наблюдения  не зависит от
не зависит от  .
.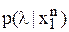 и функцией потерь
и функцией потерь 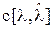 .
.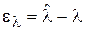 . При этом наиболее распространенными являются квадратичная, простая и модульная функции, имеющие соответственно вид:
. При этом наиболее распространенными являются квадратичная, простая и модульная функции, имеющие соответственно вид: .
.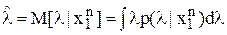 ;
; ,
,
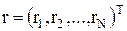 .
.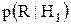 и
и 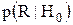 . Цель заключается в том, чтобы использовать эту информацию для выработки соответствующего правила решения. Для этого необходимо рассмотреть различные критерии принятия решения.
. Цель заключается в том, чтобы использовать эту информацию для выработки соответствующего правила решения. Для этого необходимо рассмотреть различные критерии принятия решения.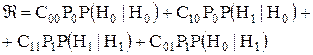 .
.
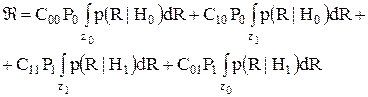 .
.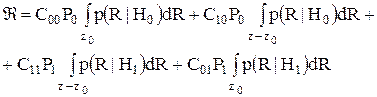 .
.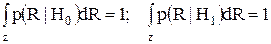 ,
,
 ,
,
 :
: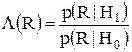 .
. .
.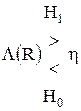 .
.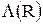 и априорные вероятности и стоимости на нее влияния не оказывают, а «приемник-обнаружитель (различитель)» можно построить, рассматривая
и априорные вероятности и стоимости на нее влияния не оказывают, а «приемник-обнаружитель (различитель)» можно построить, рассматривая 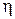 как переменный порог, учитывающий изменения в наших оценках априорных вероятностей и стоимостей.
как переменный порог, учитывающий изменения в наших оценках априорных вероятностей и стоимостей.
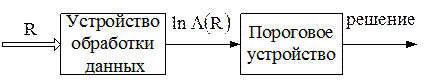
 .
.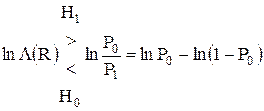 .
.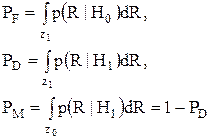 .
.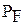 называют вероятностью ошибки первого рода (уровнем значимости критерия), вероятность
называют вероятностью ошибки первого рода (уровнем значимости критерия), вероятность 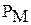 - вероятностью ошибки второго рода,
- вероятностью ошибки второго рода,  - мощностью критерия.
- мощностью критерия. .
.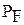 называют вероятностью ложной тревоги,
называют вероятностью ложной тревоги,  - вероятностью правильного обнаружения.
- вероятностью правильного обнаружения. и построим критерий, максимизирующий PD (или минимизирующий Рм) при указанном ограничении. Решение этой задачи легко получить, используя метод множителей Лагранжа. Построим функцию F:
и построим критерий, максимизирующий PD (или минимизирующий Рм) при указанном ограничении. Решение этой задачи легко получить, используя метод множителей Лагранжа. Построим функцию F: 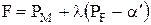
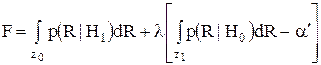 .
.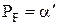 минимизация F ведет к минимизации РМ
минимизация F ведет к минимизации РМ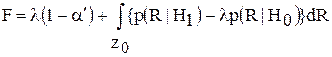 .
.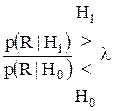 или
или 
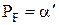 . Если обозначить плотность вероятности величины l при условии, что верна гипотеза Н0, через
. Если обозначить плотность вероятности величины l при условии, что верна гипотеза Н0, через 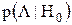 , то этот выбор равносилен требованию, чтобы
, то этот выбор равносилен требованию, чтобы  .
.


