
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Практика 7 и 8 (неделя с 5 по 11 октября).
Задача 58. Решить систему уравнений Решение. Составим расширенную матрицу.
Получили эквивалентную систему:
тогда из предпоследнего Ответ.
Задача 59. Решить систему уравнений Решение. Во-первых, можно всё 2-е уравнение сократить на 2, так удобнее для решения, числа будут меньше. Затем обнуляем ниже углового элемента: вычитаем из 2-го уравнения удвоенное 1-е, а также 3-го 1-е.
Перепишем снова в виде системы:
А из 1-го Ответ.
Неопределённые системы ( Задача 60. Решить неоднородную систему Решение. Запишем расширенную матрицу, вычтем из 2-й строки 1-ю. Здесь всего две строки, так что метод Гаусса проводится достаточно коротко.
Видим, что базисный минор можно выбрать в первых двух столбцах. Получается, что 3-я переменная свободная. Перепишем снова в виде системы, а не матрицы.
Выражаем
общее решение системы: Также записывается в виде вектора: Задавая какое-либо значение Ответ. Общее решение Заметим, что разности любых двух частных решений здесь пропорциональны вектору Задача 61. Решить систему уравнений Решение. Запишем расширенную матрицу и преобразуем её методом Гаусса:
Из 2-й строки отняли 1-ю, из 3-й удвоенную 1-ю. Замечаем, что 2 и 3 строка одинаковы, вычитаем из 3-й 2-ю, и 3-я строка получилась состоящей из 0. Это уравнение 0 = 0, очевидно, его можно вычеркнуть. Базисный минор 2 порядка можно найти в левом верхнем углу. Здесь m = 3, n = 4, r = 2. Обратите внимание. Типичной и характерной ошибкой является то, что вычёркивают обе пропорциональных строки, а не одну. Но если провести алгоритм Гаусса до конца, то видно, что одна из них остаётся и несёт содержательную информацию, а её копия лишняя, она обратилась в 0. Не нужно торопиться и вычёркивать все пропорциональные строки, ведь хотя бы одна из них не лишняя!
Развернём две оставшихся строки снова в систему уравнений:
Здесь перенесём
Просто справа при этом не только константы, а составные выражения из констант и каких-то параметров. Видно, что
Его можно записать также и в виде такого вектора: Если задавать любое Например, при Ответ. Общее решение Домашняя задача. Решить неоднородную систему Ответ. Общее решение Задача 62. Решить неоднородную систему.
Решение. Построим и преобразуем расширенную матрицу.
Базисный минор в первых двух столбцах, последние две переменные свободные, переносим их вправо.
Отсюда
Ответ. Общее решение:
Задача 63. Решить неоднородную систему Решение. Запишем расширенную матрицу системы.
обнулим всё ниже углового элемента, для этого: из 2-й строки вычтем 1-ю, из 3-й удвоенную 1-ю, из 4-й 1-ю, домноженную на 4.
теперь можно поменять местами 2 и 3 строки, а также домножить на
затем из 4-й строки вычитаем 2-ю, чтобы продолжить стандартную процедуру метода Гаусса, потом видим что 3-я и 4-я стали одинаковы, тогда из 4-й вычитаем 3-ю. Получается, что 4-е уравнение 0 = 0.
Итак, осталось 3 уравнения, базисный минор легко заметить в первых трёх столбцах (там треугольная структура матрицы, и этот определитель явно отличен от 0). 4-й столбец не входит в базисный минор, то есть 4-я переменная свободная, т.е. когда будем записывать систему, переносим её через знак равенства во всех уравнениях.
Из последнего уравнения
Можно записать в виде вектора: Если задать, например, Ответ. Общее решение:
|
||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 105; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.109.30 (0.014 с.) |
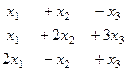

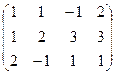
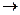

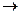
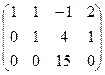
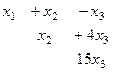
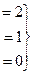 , из последнего уравнения, очевидно,
, из последнего уравнения, очевидно, 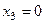 ,
,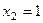 , и из 1-го
, и из 1-го 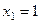 .
.  .
. 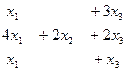

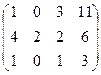
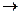
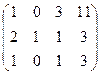
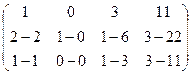 =
=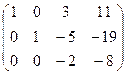 треугольная структура уже получилась.
треугольная структура уже получилась.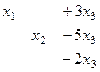
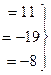 из 3-го уравнения
из 3-го уравнения 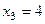 , подставляем во 2-е, там получается
, подставляем во 2-е, там получается 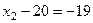
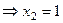 .
.
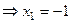 .
.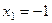 ,
, 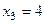 .
.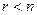 ).
).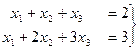
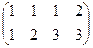
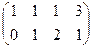
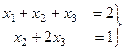 переносим
переносим 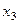 вправо:
вправо: 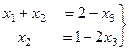
 , а затем поднимаемся в 1-е уравнение и
, а затем поднимаемся в 1-е уравнение и 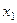 ,через константы и
,через константы и 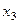 . Впрочем,
. Впрочем, 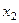 фактически и так уже выражено:
фактически и так уже выражено: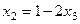 . Подставим это выражение в 1-е уравнение
. Подставим это выражение в 1-е уравнение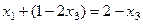 , тогда
, тогда 
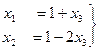
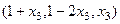 .
. , всякий раз можем вычислить остальные переменные, и получить тройку чисел. Частные решения: (1,1,0) или (2,-1,1) или (3,-3,2)... их бесконечно много.
, всякий раз можем вычислить остальные переменные, и получить тройку чисел. Частные решения: (1,1,0) или (2,-1,1) или (3,-3,2)... их бесконечно много.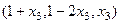 .
. .
. .
.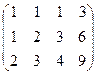
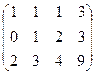

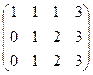
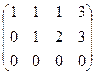 .
.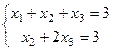
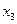 вправо, 3-я переменная - свободная, базисный минор в левом углу. Замечание. Впрочем, это не единственный вариант: базисный минор можно составить из фрагментов 1 и 3 столбца, тогда
вправо, 3-я переменная - свободная, базисный минор в левом углу. Замечание. Впрочем, это не единственный вариант: базисный минор можно составить из фрагментов 1 и 3 столбца, тогда 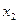 была бы свободная. Итак, перенесём
была бы свободная. Итак, перенесём  :
: Основная матрица системы фактически стала квадратной, 2 порядка, т.е. множество коэффициентов при базисных переменных образует такую квадратную матрицу:
Основная матрица системы фактически стала квадратной, 2 порядка, т.е. множество коэффициентов при базисных переменных образует такую квадратную матрицу: 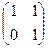 .
.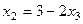 . Подставим это выражение в 1-е уравнение, чтобы выразить отдельно
. Подставим это выражение в 1-е уравнение, чтобы выразить отдельно 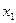 через
через 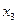 .
.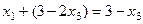 в итоге
в итоге 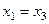 . Итак,
. Итак, 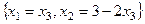 - общее решение. В нём есть один свободный параметр
- общее решение. В нём есть один свободный параметр 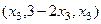 .
.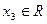 , будет получать тройки чисел, которые служат частными решениями.
, будет получать тройки чисел, которые служат частными решениями. .
.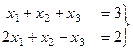
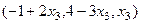 .
.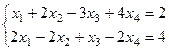
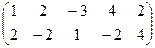
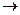
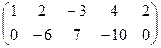
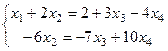
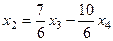 . Тогда
. Тогда  =
= =
= 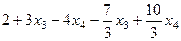 =
= .
.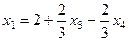 ,
, 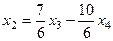 .
.

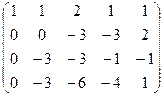
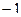 три последних уравнения (там почти везде были знаки минус)
три последних уравнения (там почти везде были знаки минус)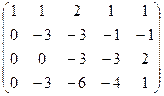
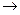
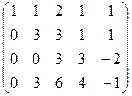
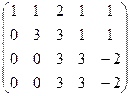

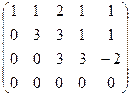
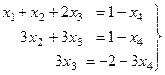
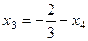 , подставляя это выражение во 2-е уравнение, выразим
, подставляя это выражение во 2-е уравнение, выразим 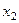 .
. 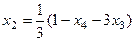 =
=  ,
,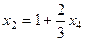 . Далее из 1-го уравнения:
. Далее из 1-го уравнения: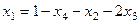 =
= 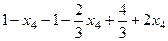 ,
, . Итак, общее решение:
. Итак, общее решение: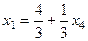 ,
, 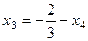 .
.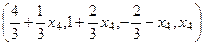 .
.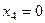 получим частное решение:
получим частное решение: 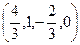 .
.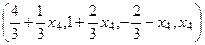 .
.


