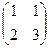Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Практики 1 и 2 (неделя с 14 по 20 сентября).Стр 1 из 7Следующая ⇒
Приходовский М.А. Математика Курс практических занятий Семестр 1 Группы 520, 530 Томск ТУСУР 2020 Практики 1 и 2 (неделя с 14 по 20 сентября). Действия над матрицами. Задача 1. Найти сумму и разность матриц: Решение. Складываем поэлементно:
Вычитаем:
Ответ. Сумма: Задача 2. Найти сумму матриц: Решение. Складываем поэлементно:
Ответ. Задача 3. Даны матрицы Найти Решение. Запишем эти матрицы. Если первую разбить на строки, а вторую на столбцы, то видно, что есть всего 4 варианта скалярно умножить друг на друга вектор-строку их первой на вектор-столбец из второй.
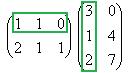
Например, если умножаем строку номер 1 на столбец номер 2, то и число, которое при этом получается, ставим в 1 строку 2 столбец новой матрицы. Итак,
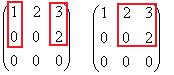
Теперь найдём Покажем, например, как 1-я строка скалярно умножается на 1-й столбец, они обведены.
Ответ. Задача 4. Найти произведение матриц: а) Решение.
Ответ. Примечания. 1) Видим, что в общем случае может не выполняться закон коммутативности при умножении матриц, то есть 2) При умножении на матрицу, состоящую из всех единиц, исходная не получается, а вот если единицы по диагонали - получается. Матрица Задача 5. Дана матрица Решение. Умножим матрицу саму на себя, то есть две её копии напишем рядом и умножим их.
Как видно из этого примера, для матриц, в отличие от чисел, возможно, что получается нулевой объект в ответе, притом что в исходной матрице вообще ни одного нуля не было. Это из-за особенностей её строения: правый столбец в 2 раза меньше, чем левый, а нижняя строка в минус 2 раза больше, чем верхняя. И вообще, если взять пару матриц, где у первой будет пропорциональность строк (в k раз больше) а у второй - столбцов (в минус k раз меньше) получим такой же эффект. Задача 6. Даны матрицы Решение.
Ответ.
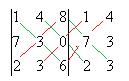
Задача 7. Найти произведение матриц
Решение. Размеры согласованы: длина строки 1-й матрицы равна высоте столбца 2-й матрицы. Первую можно мысленно разрезать на 2 строки, вторую на 3 столбца. Итого будет 6 различных произведений строк на столбцы.
Задача 8. Вычислить Заметим, что получаются 1-й и 2-й столбец матрицы.
Замечание. При умножении квадратной матрицы на вектор-столбец получается снова вектор-столбец, то есть квадратная матрица фактически выступает в роли функции, отображающей векторы в пространстве (или на плоскости, если n = 2). Коротко о понятии линейного оператора и строении его матрицы и о том, что при умножении на i-й базисный вектор получается столбец номер i. Задача 9А. Найти произведение: Задача 9Б. Решение. В 1-м случае размеры
Для пункта «Б» 1-я и 2-я строка умножаются не только на 1-й и 2-й, но ещё и на 3-й столбец. Дополнительно получаем
Выделим красным цветом новый столбец:
Ответ. 9А: Задача 10. Даны матрицы
Решение. Так как матрица С находится справа во всех слагаемых, то для удобства можно использовать приведение подобных Сначала запишем
Теперь умножим на матрицу С. Точно так же, как и в прошлом примере, мысленно обведём строку из 1-й матрицы на столбец из 2-й. Есть 4 варианта это сделать:
Ответ. Задача домашняя 1. Найти произведение Ответ.
Задача дом-2. Ответ. Задача дом-3. Ответ. Задача 11. Дана матрица Решение. Сначала умножим две, и найдём
Теперь домножим ещё на одну матрицу А, чтобы найти
Ответ. Замечание. Несмотря на то, что в общем случае коммутативности по умножению матриц нет, но если матрица
Задача дом-4. Найти Задача 12. Найти произведение
Решение. Вычислим
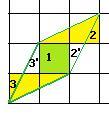
Замечание. Если вычислять Определители. Задача 13. Для параллелограмма, построенного на базе системы векторов (2,1) и (1,2), площадь равна 3. Если область 2’ перенести в область 2, то видно, что получается половина прямоугольника площади 2 (выделено жёлтым). То есть площадь равна 1. Аналогично 3’ в 3. Там тоже площадь 1. Кроме того, в центре квадрат площади 1.
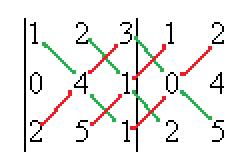
Практика 2. Задача 14. Найти определитель Решение. Ответ. 18. Задача 15. Найти определитель Решение. Допишем копии первых двух столбцов, проведём 3 параллельных линии (главная диагональ и ещё две). Перемножим все эти тройки элементов и внесём в общую сумму с их исходным знаком. А вот для побочной диагонали и линий, ей параллельных, со сменой знака.
Ответ.
Задача 16. Найти определитель Решение.
То, что перемножено по зелёным линиям, включим в сумму со знаком плюс, а по красным - со знаком минус.
Ответ. 5. Задача 17. Найти определитель Решение.
Задача 18. Найти определитель Решение.
Задача 19. Найти определитель Решение.
Задача Дом-1. Вычислить определитель Задача 20. Вычислить определитель Решение. Заметим, что 1-й и 3-й столбец содержат очень похожие группы элементов а именно 1 и 2. Вычтем из 1-го столбца 3-й, а затем разложим по 1-му столбцу.
Ответ. 24. Задача дом-2. Вычислить определитель
Решение. Первый способ. Разложение по 1-й строке:
Очевидно, что последние 2 минора 3-го порядка вычислять не надо, так как они умножаются на 0. Осталось вычислить два минора 3 порядка, то есть мы свели определитель 4 порядка к определителям 3 порядка.
Ответ. 0. Второй способ. Из 2-го столбца вычтем 1-й
А теперь разложим по 1-й строке, причём реально для вычисления останется только один минор третьего порядка.
Ответ. 0. Задача 27. Вычислить определитель Решение. Можем разложить по 1-й строке (там всего 2 элемента отличны от 0). Но можно сначала упростить матрицу, а именно, отнять от 4 столбца 1-й столбец. Тогда в 1-й строке будет всего один ненулевой элемент. Также выносим
Ответ. Задача 28. Вычислить определитель Решение. В последней строке, а также в последнем столбце, столбце видим 2 нуля и 2 ненулевых элемента. Можно сделать так, чтобы было 3 нулевых элемента. Прибавим удвоенную 3-ю строку ко 2-й:
Теперь можно от 3-го столбца отнять 2-й, умноженный на 8.
а далее разложить по последней строке:
вынесем общий множитель 4 из 1 столбца:
Ответ. 1212.
Решение. Метод 1. Выбираем окаймляющие миноры, начиная от левого верхнего угла. Видно, что минор 2 порядка не равен 0, поэтому ранг больше или равен 2. Вычисляя минор 3 порядка (а он здесь единственный, это и есть сам определитель матрицы) видим, что он равен 0.
Метод 2. Преобразуем матрицу к треугольному виду. Вычитаем из 2-й строки 1-ю, и из 3-й удвоенную 1-ю.
Теперь 2-ю строку, умноженную на 0,5, прибавим к 3-й.
Теперь видно, что 3-я строка состоит из нулей, поэтому ранг не может быть равен 3. Минор 2-го порядка тоже сразу виден, это Ответ.
Задача 33. Найти ранг матрицы Решение. Вычтем из 2-й строки 1-ю, а из 3-й удвоенную 1-ю.
Во-первых, сразу видно, что есть угловой минор порядка 2, отличный от нуля. Ближайший окаймляющий для него содержит столбец из нулей, однако это ещё не значит, что ранг не может быть равен 3. Если рассмотреть другой окаймляющий минор, а именно, состоящий из 1,2 и 4 столбцов, то увидим, что ранг равен 3.
Ответ. Задача 34. Найти ранг матрицы Решение.
Теперь 2-ю строку, домноженную на 10, прибавим к 3-й.
Итак, исходная матрица сводится к такой, в которой уже есть треугольная структура в первых трёх столбцах.
Очевидно, что обведённый минор равен 46, не равен 0. Он 3-го порядка, поэтому ранг равен 3. Ответ. Задача 35. Найти ранг матрицы и базисный минор. Решение. Преобразуем матрицу:
Сначала из 2 строки вычитаем 1-ю, домноженную на 2, то есть вычитаем строку (2 4 6) а из 3-й 1-ю, домноженную на 5, т.е. строку (5 10 15). Затем к 3-й прибавляем 2-ю с коэффициентом 7. Видно, что базисный минор не может быть в левом верхнем углу, потому что во 2-й строке два нуля. Зато можно найти минор 2 порядка, состоящий из частей 10и 3 столбца, либо 2 и 3-го.
Минор порядка 3, то есть сам определитель всей этой матрицы, равен 0, так как третий столбец содержит только нули. Поэтому ранг равен 2, а не 3. Ответ. Практики 5 (до № 46) и 6 (до № 57). (неделя с 28 сентября по 4 октября). Задача 36. Найти ранг матрицы Решение. Преобразуем матрицу. Ко второй строке прибавим 1-ю, а от 3-й отнимем удвоенную 1-ю. теперь к третьей прибавим вторую, получим Ранг равен 3, так как есть невырожденный минор 3 порядка. Ответ. Задача 36-А (вариант прошлой задачи, но с параметром).
Найти параметр
Решение. Третья строка состояла бы из всех нулей, только если
Задача 37. Найти ранг матрицы Решение. Преобразуем методом Гаусса к треугольной форме.
Видно, что 4-я строка из нулей, поэтому ранг не равен 4, то есть
Этот минор невырожденный, и он тоже является окаймляющим (ведь он полностью включает в себя квадрат, закрашенный жёлтым). Мы нашли базисный минор порядка 3. Также можно было рассматривать аналогичное в 1,2,5 столбцах, тоже минор порядка 3. Ответ. Задача 38. Найти такие параметры
Решение. Вычтем из 2-го столбца удвоенный 1-й. Затем из 3-го утроенный 1-й.
Если Задача 39. Найти ранг матрицы.
Решение. Для удобства преобразования методом Гаусса, сначала поменяем местами 1 и 3 строки. Ещё можно сразу прибавить 3-ю строку к 4-й.
Дальше стандартным методом, обнулим всё ниже угла.
Для удобства вычислений домножим 2 строку на (-1), ранг при этом не меняется. Затем прибавим к 3 строке удвоенную 2-ю.
Теперь осталось прибавить к 4 строке удвоенную 3-ю.
Ответ. Задача 39-А. Найти значение параметра
Решение. Выполняя преобразования, аналогичные тем, что в прошлой задаче, получим
Задача 40. Найти А) Решение. Пункт А).
Из 2-й строки вычли удвоенную 1-ю, из 3-й 4-кратную 1-ю. Затем домножили 3-ю на 4, чтобы стало кратное число (20). Затем из 3-й отняли 5-кратную 2-ю. Видим, что независимо от Б) Если нет 3-го столбца (по сравнению с прошлым пунктом), то удастся найти
Последняя строка состоит из нулей при Ответ. А) не существует Б) Обратная матрица. Формула вычисления элементов обратной матрицы: Алгоритм нахождения 1. Проверить невырожденность с помощью определителя. 2. Составить матрицу из дополняющих миноров Mij. 3. Изменить знаки в шахматном порядке, то есть домножить на (-1)i+j, где i,j - номера строки и столбца. 4. Транспонировать полученную матрицу. 5. Поделить на определитель исходной матрицы. Задача 41. Найти Решение. Матрица из миноров: Матрица из алг. дополнений: Транспонируем её: Делим её на определитель, и записываем ответ: Ответ. Можно сделать проверку:
Задача 42. Найти обратную матрицу для Решение. 1). Проверяем определитель 2) Составляем матрицу из дополняющих миноров, то есть для каждой клетки вычёркиваем строку и столбец, остаётся подматрица порядка 1, то есть то число, которое напротив, как раз и является дополняющим минором. Получаем 3) В шахматном порядке меняем знак там, где i+j нечётное. Тем самым, мы переходим от 4) Транспонируем эту матрицу. 5) Определитель был равен 1. Делить на 1 не обязательно, можно автоматически считать, что уже и так разделили. Проверка:
Задача 43 (теор). Доказать, что не существует различных матриц «обратной слева» и «обрат
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 131; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.147.190 (0.196 с.) |
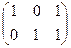 +
+ 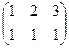
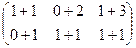 =
= 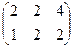 .
.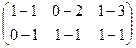 =
= 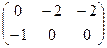 .
.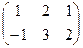 +
+ 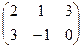
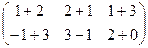 =
= 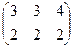 .
.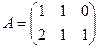 ,
, 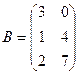 .
. 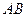 и
и 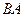 .
.
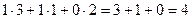
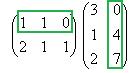
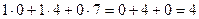
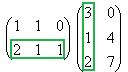
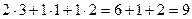
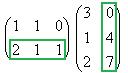
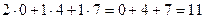
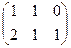
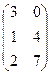 =
= 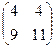 .
. 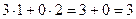 .
.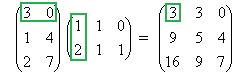
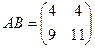
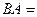
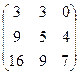 .
. 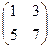
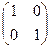 , б)
, б) 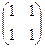 , в)
, в) 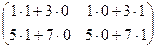 =
= 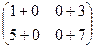 =
= 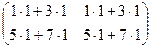 =
= 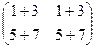 =
= 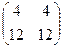 .
.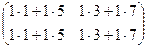 =
= 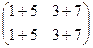 =
= 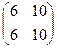 .
.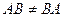
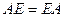 .
.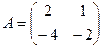 найти
найти 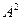 .
.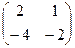
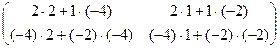 =
=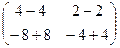 =
=  . Ответ.
. Ответ. 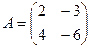
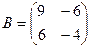 . Найти
. Найти 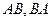 .
.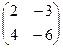
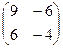 =
= 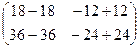 =
= 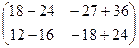 =
= 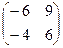 .
.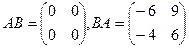 .
.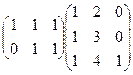 .
.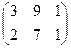 . Ответ.
. Ответ. 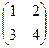
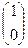 и
и 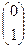 .
.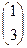 ,
, 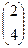 .
.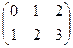
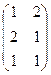 .
.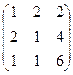 .
.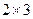 и
и 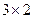 , согласованы, умножение возможно. Во 2-м случае
, согласованы, умножение возможно. Во 2-м случае 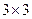 , тоже согласованы (хоть столбцов и больше, но всё равно длина строки 1-й матрицы равна высоты столбца 2-й матрицы). Просто в ответе для 3Б получится ещё один лишний столбец справа.
, тоже согласованы (хоть столбцов и больше, но всё равно длина строки 1-й матрицы равна высоты столбца 2-й матрицы). Просто в ответе для 3Б получится ещё один лишний столбец справа.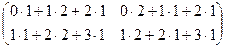 =
=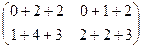 =
= 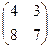 .
.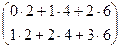 =
= 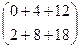 =
= 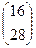 .
.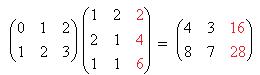
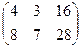 .
.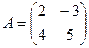 ,
, 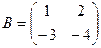 ,
, 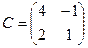 . Найти
. Найти 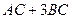 .
. 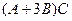 - тогда умножение надо будет проводить всего один раз, а не два.
- тогда умножение надо будет проводить всего один раз, а не два.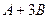 .
.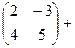
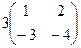 =
= 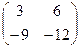 =
= 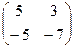 .
.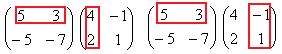
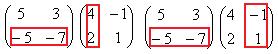
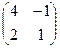 =
= 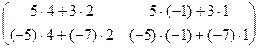 =
= 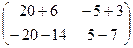 =
= 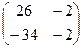 .
. 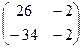 .
. 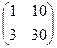
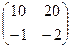 .
.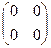 .
.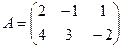
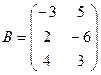 Найти
Найти  .
. 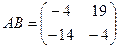 ,
, 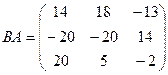 .
.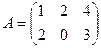
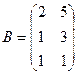 . Найти
. Найти 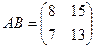 ,
, 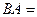
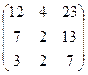 .
.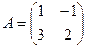 . Найти
. Найти 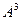 .
. 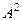 .
.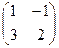
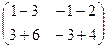 =
= 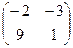 .
.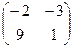
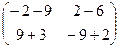 =
=  .
.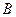 совпадает с матрицей
совпадает с матрицей 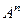 , тогда
, тогда 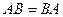 . Например, в этой задаче,
. Например, в этой задаче, 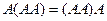 из-за ассоциативности, т.е. неважно, домножить третий раз слева или справа.
из-за ассоциативности, т.е. неважно, домножить третий раз слева или справа.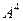 для этой же матрицы. Замечание. Здесь есть 2 метода решения: либо умножить
для этой же матрицы. Замечание. Здесь есть 2 метода решения: либо умножить 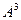 , полученную в прошлой задаче, ещё раз на
, полученную в прошлой задаче, ещё раз на 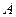 , либо взять
, либо взять 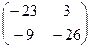 .
.  , где
, где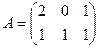 ,
, 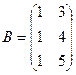 ,
, 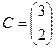 .
.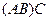 , сначала умножим первые две матрицы:
, сначала умножим первые две матрицы: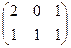
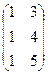 =
= 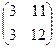 . Теперь умножим на третью матрицу.
. Теперь умножим на третью матрицу.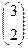 =
= 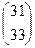 . Ответ.
. Ответ.  , то получается точно такой же результат, т.к. выполняется закон ассоциативности.
, то получается точно такой же результат, т.к. выполняется закон ассоциативности.  =
=  .
. 
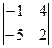 .
.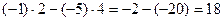 .
.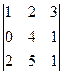
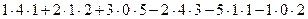 =
=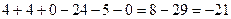 .
.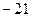 .
.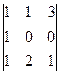 .
.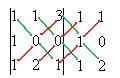
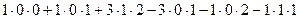 =
= 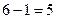 .
.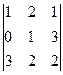 .
. 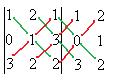
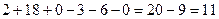 . Ответ. 11.
. Ответ. 11. 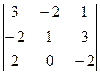 .
.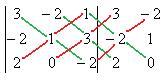
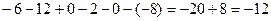 . Ответ.
. Ответ. 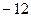 .
.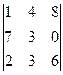 .
.
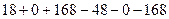 =
= 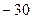 . Ответ.
. Ответ. 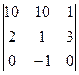 . Ответ. 28.
. Ответ. 28.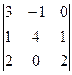 .
.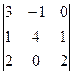 =
= 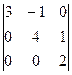 =
= 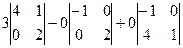 =
=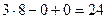 .
.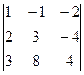 . Ответ. 50.
. Ответ. 50.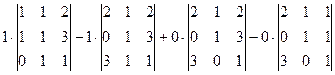
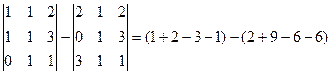 =
= 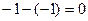 .
.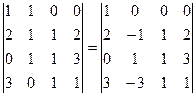
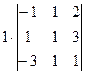 . Теперь ко 2-й строке прибавим 1-ю а из 3-й вычтем утроенную 1-ю. А затем уже к 3-й строке прибавляем 2-ю.
. Теперь ко 2-й строке прибавим 1-ю а из 3-й вычтем утроенную 1-ю. А затем уже к 3-й строке прибавляем 2-ю.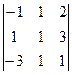 =
= 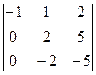 =
= 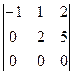 = 0.
= 0.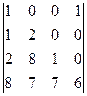 .
.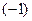 из последнего столбца.
из последнего столбца.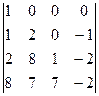 =
= 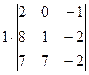 =
= 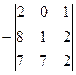 =
=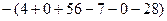 =
= 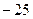 .
.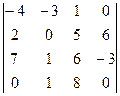 .
.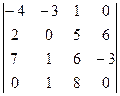 =
= 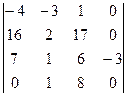 , теперь разложим по последнему столбцу, будет нужно вычислить всего 1 из 4 миноров порядка 4, так как остальные умножаются на 0.
, теперь разложим по последнему столбцу, будет нужно вычислить всего 1 из 4 миноров порядка 4, так как остальные умножаются на 0.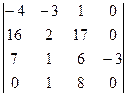 =
= 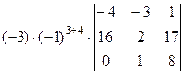 =
= 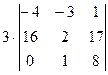 .
.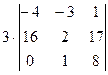 =
= 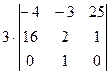
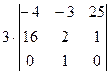 =
= 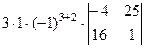 =
= 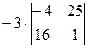 ,
,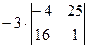 =
= 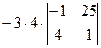 =
= 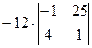 =
= 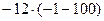 =
= 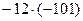 =
= 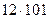 = 1212.
= 1212.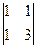
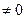 .
.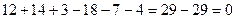 . Тогда ранг не равен 3.
. Тогда ранг не равен 3.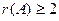 , но при этом
, но при этом 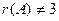 . Остаётся единственный вариант:
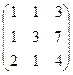
. Остаётся единственный вариант: 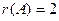 .
.
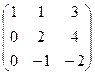
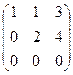
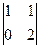
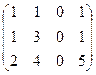 .
.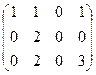 теперь из 3-й вторую:
теперь из 3-й вторую: 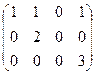 .
.
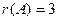 .
.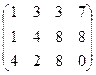 .
.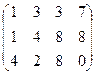
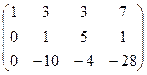
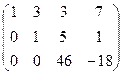 .
.
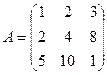 .
.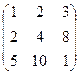
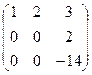
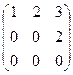
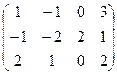 .
.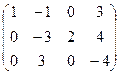
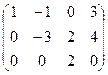 .
.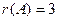 .
. 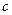 , при котором ранг матрицы равен 2:
, при котором ранг матрицы равен 2: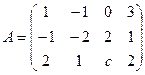
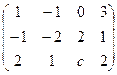
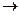
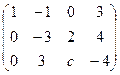
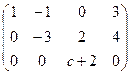
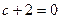 , то есть
, то есть 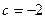 . Ответ.
. Ответ. 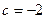 .
.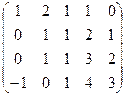 .
.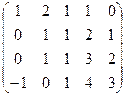
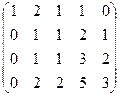
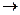
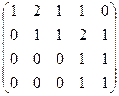
 .
.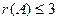 . Минор порядка 2 легко находится в верхнем левом углу, но угловой минор порядка 3 равен 0. Однако это ещё не значит, что ранг равен 2, ведь можно отступить к правому краю матрицы и взять минор с разрывом, из 1,2,4 столбцов, например такой:
. Минор порядка 2 легко находится в верхнем левом углу, но угловой минор порядка 3 равен 0. Однако это ещё не значит, что ранг равен 2, ведь можно отступить к правому краю матрицы и взять минор с разрывом, из 1,2,4 столбцов, например такой: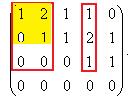
 , что ранг матрицы равен 1:
, что ранг матрицы равен 1: 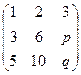
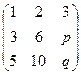
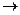
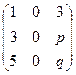
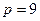 и
и 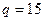 , то последний столбец состоит только из нулей, и ранг будет равен 1. Ответ.
, то последний столбец состоит только из нулей, и ранг будет равен 1. Ответ. 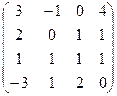
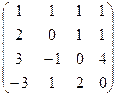
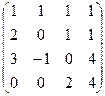
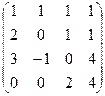
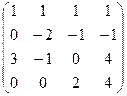
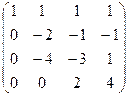
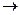
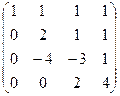
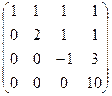 . Видно, что получилась треугольная матрица, то есть определитель 4 порядка невырожденный. Поэтому
. Видно, что получилась треугольная матрица, то есть определитель 4 порядка невырожденный. Поэтому 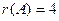 .
.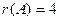 .
. 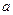 , при котором ранг матрицы был бы равен 3.
, при котором ранг матрицы был бы равен 3.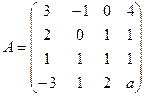
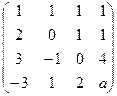
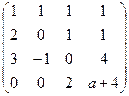
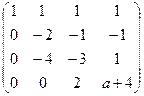
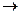
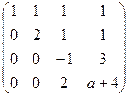
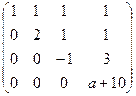 . Только в том случае, когда
. Только в том случае, когда 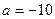 , последняя строка состоит из нулей, и ранг равен 3, а не 4. Ответ.
, последняя строка состоит из нулей, и ранг равен 3, а не 4. Ответ. 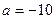 .
.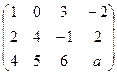 Б)
Б) 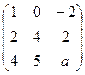
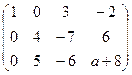
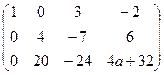
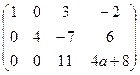
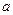 и от последнего столбца, есть невырожденный минор в первых 3 столбцах. Поэтому ни при каком
и от последнего столбца, есть невырожденный минор в первых 3 столбцах. Поэтому ни при каком 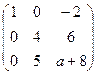
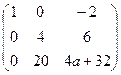
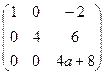
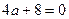 , т.е.
, т.е. 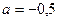 .
. 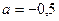 .
. 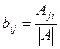 .
.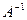 .
.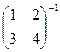 .
. 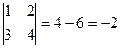 . Вывод:
. Вывод: 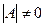 , существует обратная матрица.
, существует обратная матрица.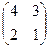 .
.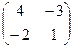 .
.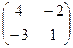 .
.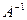 =
= 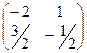 .
. 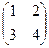
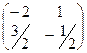 =
= 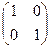 .
.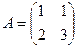 .
.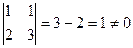 , так что обратная матрица существует.
, так что обратная матрица существует.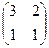 .
.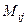 к
к 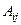 . Получили
. Получили 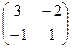 .
.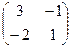 .
.