
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Миноры и алгебраические дополнения элементов.
Определители n -го порядка Определители квадратных матриц второго и высшего порядков вычисляются методом разложения определителя по элементам строки (столбца). Для этого вводятся понятие минора и алгебраического дополнения элемента матрицы. Минором Мij элемента аij квадратной матрицы А порядка n ≥ 2 называется определитель (n-1)-го порядка, полученный из элементов матрицы А (без изменения их распо ложения) путем вычеркивания i –й строки и j – го столбца, на пересечении которых находится элемент аij Алгебраическим дополнением (адъюнктом) Аij элемента аij называется число, определяемое равенством Аij = (-1)i+jMij. Тогда определители второго и третьего порядков вычисляются методом разложения по элементам какой-нибудь строки (какого-нибудь столбца). Например: вычисление определителя второго порядка сведется к вычислению определителей первого порядка, а вычисление определителя третьего порядка – к вычислению определителей второго порядка. Определитель n-го порядка введем по определению как разложение по элементам первой строки:
Формула позволяет вычислить определитель n-го порядка через определители (n-1)-го порядка, постепенно снижая порядок до вычисления определителей второго порядка. Доказывается, что определитель n-го порядка можно вычислять разложением поэлементам любой его строки (любого его столбца). На практике надо вычислять определитель разложением по элементам той строки (того столбца), в которой (в котором) имеется больше всего нулей, т.к. это позволяет не вычислять миноры Мij тех элементов аij, которые равны нулю.
Свойства определителей Свойство 1. Определитель не меняется при транспонировании, т.е. Δ(А)= Δ(А^T). Свойство 2. При перестановке двух строк (или столбцов) определитель меняет знак.(Для определителей 3го порядка свойство можно доказать непосредственным применением правила треугольника.) Свойство 3. (для определителей 2го и 3го порядка). Определитель n-го порядка = сумме произведений элементов любой строки на соответствующие им алгебраические дополнения.
Свойство 4. Определитель у которого две строки одинаковы = 0. Свойство5. Если все элементы какой-либо строки определителя = 0, то и определитель =0.(Это св-во вытекает из свойства 3, только нужно разложить этот определитель по элементам его нулевой строки.)
Свойство6. Если все элементы какой-нибудь строки определителя умножить на одно и то же число альфа, то значение определителя умножится на это число. Свойство7. Определитель у которого элементы 2х строк соответственно пропорциональны = 0. Свойство8. Пусть каждый элемент i-ой строки определителя есть сумма 2х слагаемых: Aij = bj + cj (j=1,…,n) Тогда заданный определитель = сумме 2х определителей: у одного из них i-ая строка состоит из элементов bj, а у другого- из элементов cj; все остальные строки этих 2х опред-й, кроме i-ой, имеют такие же элементы, как и исходный определитель Свойство9. Определитель не изм-ся, если к элементам какой-нибудь строки прибавить соответствующие элементы другой строки, умноженные на одно и то же число. Свойство10. Сумма произведений элементов какой-нибудь строки определителя на алгебраические дополнения соответствующих элементов другой строки = 0, т.е. ai1Aj1+ai2Aj2+…+ainAjn=0 (i≠j) Доказательство. Пусть Δ(А) - определитель квадратной матрицы А. Заменим в матрице А j-ю строчку её i-ой строчкой, а все остальные строки, включая i-ю, оставим без изменения. В результате получим новую матрицу В, у которой i-я и j-я строки совпадают. По свойству 4 опр-ль этой матр =0: Δ(В)=0. Теперь вычислим определитель матрицы В разложением по элементам j-ой строки. При этом учтем, что миноры элементов j-й строки матрицы В совпадают с минорами соответствующих элементов j-й строки матрицы А. Тогда совпадают и алгебр дополнения элементов j-й строки матриц А и В. В результате получим: Δ(B) = ai1Aj1+ai2Aj2+…+ainAjn Отсюда получаем 1е, т.к. ранее установлено, что Δ(В)=0. Теорема. Определитель произведения 2х матриц n-го порядка = произведению определителей этих матриц: Δ(АВ)= Δ(А)* Δ(В).
Алгоритм Гаусса Алгоритм Гаусса использует элементарные преобразования матрицы двух типов. Преобразование первого рода: две строки матрицы меняются местами, и при этом знаки всех элементов одной из строк изменяются на противоположные. Преобразование второго рода: к одной строке матрицы прибавляется другая строка, умноженная на произвольное число.
Элементарные преобразования сохраняют определитель и ранг матрицы, а также множество решений линейной системы. Алгоритм Гаусса приводит произвольную матрицу элементарными преобразованиями к ступенчатому виду. Для ступенчатой квадратной матрицы определитель равен произведению диагональных элементов, а ранг - числу ненулевых строк Метод Гаусса в математическом варианте состоит в следующем: ищем сначала ненулевой элемент в первом столбце. Если все элементы первого столбца нулевые, то переходим ко второму столбцу, и так далее. Если нашли ненулевой элемент в k-й строке, то при помощи элементарного преобразования первого рода меняем местами первую и k-ю строки, добиваясь того, чтобы первый элемент первой строки был отличен от нуля; используя элементарные преобразования второго рода, обнуляем все элементы первого столбца, начиная со второго элемента. Для этого от строки с номером k вычитаем первую строку, умноженную на коэффициент ak1/a11. переходим ко второму столбцу (или j-му, если все элементы первого столбца были нулевыми), и в дальнейшем рассматриваем только часть матрицы, начиная со второй строки и ниже. Снова повторяем пункты 1) и 2) до тех пор, пока не приведем матрицу к ступенчатому виду.
|
||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 72; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.156.212 (0.005 с.) |
 = а11 А11 + а12А12
= а11 А11 + а12А12 =
= 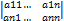 =a11A11+…+a1nA1n
=a11A11+…+a1nA1n


