
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 2.1. Выборки и их характеристикиСтр 1 из 7Следующая ⇒
Тема 2.1. Выборки и их характеристики 1. Предмет и задачи математической статистики. 2. Генеральная и выборочная совокупности. 3. Статистическое распределение выборки. 4. Эмпирическая функция распределения. 5. Графическое изображение статистического распределения. 6. Числовые характеристики статистического распределения. 7. Корреляционный анализ выборочной совокупности (оценка выборочного корреляционного момента системы двух случайных величин; регрессионный анализ двух случайных величин). Математическая статистика является частью общей прикладной математической дисциплины “Теория вероятностей и математическая статистика”, однако задачи, решаемые ею, носят специфический характер. Если теория вероятностей исследует Явления, полностью заданные их моделью, то в математической статистике вероятностная модель определена с точностью до неизвестных параметров. Отсутствие сведений о параметрах компенсируется “пробными” испытаниями, на основе которых и восстанавливается недостающая информация. Цель математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов. Первой задачей математической статистики является указание методов сбора и группировки статистических сведений, которые получены в результате экспериментов или наблюдений. Вторая задача — это разработка методов анализа статистических данных: оценки неизвестных вероятности события, а также функции и параметров распределения; оценка зависимости случайной величины от других случайных величин; проверка статистических гипотез о виде и величинах параметров неизвестного распределения. Рассмотрим некоторые из этих вопросов. Выборки На практике сплошное исследование (каждого объекта из интересующей нас совокупности) проводят крайне редко. К тому же если эта совокупность содержит большое число объектов или исследование объекта требует нарушения его функционального стандарта, то сплошное исследование нереально. В таких случаях из всей совокупности случайно отбирают ограниченное число объектов и подвергают их исследованию. Введем основные понятия, связанные с выборками.
Генеральной совокупностью называется совокупность объектов, из которых производится выборка. Выборочной совокупностью(выборкой) называется совокупность случайно отобранных объектов из генеральной совокупности. Число объектов в совокупности называется ее объемом. Пример 1. Пусть из 2000 изделий отобрано для обследования 100 изделий. Тогда объем генеральной совокупности N = 2000, а объем выборки п = 100. Выборку можно осуществлять двумя способами. Если после исследования объект из выборки возвращается в генеральную совокупность, то такая выборка называется повторной; если объект не возвращается в генеральную совокупность, то выборка называется бесповторной. Выборка называется репрезентативной (представительной), если по ее данным можно достаточно уверенно судить об интересующем признаке генеральной совокупности. Способы отбора Различают два способа отбора: без расчленения генеральной совокупности на части и с расчленением. К первому относятся простые случайные отборы (либо повторный, либо бесповторный), когда объекты извлекают по одному из всей генеральной совокупности; такой отбор можно производить с использованием таблицы случайных чисел. Второй способ отбора включает следующие разновидности, соответствующие способам расчленения генеральной совокупности. Отбор, при котором объекты отбираются из каждой “типической ” части генеральной совокупности, называется типическим. Например, отбор деталей из продукции каждого станка, а не из их общего количества является типическим. Если генеральную совокупность делят на число групп, равное объему выборки, с последующим отбором из каждой группы по одному объекту, то такой отбор называется механическим. Серийным называется отбор, при котором объекты отбираются не по одному, а сериями; этот способ используется, когда исследуемый признак имеет незначительные колебания в различных сериях. На практике часто употребляется комбинирование указанных выше способов отбора. Например, генеральную совокупность разбивают на серии одинакового объема, затем случайным образом отбирают несколько серий и в завершение случайным извлечением отдельных объектов составляют выборку. Конкретная комбинация способов отбора объектов из генеральной совокупности определяется требованием репрезентативности выборки.
Таким образом на выборку будем смотреть как на совокупность независимых случайных величин x 1, x 2,..., x n, распределенных так же, как и случайная величина x, представляющая генеральную совокупность. Выборочные значения x 1, x 2,..., xn – это значения, которые приняли эти случайные величины в результате 1-го, 2-го,..., n -го эксперимента. Полигон и гистограмма Каждую пару значений (х i, ni) из распределения выборки можно трактовать как точку на координатной плоскости. Точно так же можно рассматривать и пары значений (xi, Wi) относительного распределения выборки. Ломаная, отрезки которой соединяют точки (х i, ni), называется полигоном частот. Ломаная, соединяющая на координатной плоскости точки (xi, Wi), называется полигоном относительных частот. На рис. 15.9 показан полигон относительных частот для распределения, приведенного в примере 2.
Для случая непрерывного признака X удобно разбить интервал (xmin, xmax) его наблюдаемых значений на несколько частичных интервалов длиной h каждый и найти для каждого из этих интервалов сумму частот nj, попавших в него. Ступенчатая фигура, состоящая из прямоугольников с основаниями длиной h и высотами nj / h (плотность частоты), называется гистограммой частот. Геометрический смысл гистограммы: нетрудно видеть, что площадь ее равна сумме всех частот или объему выборки. На рис. 15.10 изображена гистограмма объема п = 100.
Выборочную дисперсию можно считать точечной оценкой дисперсии D x генеральной совокупности. Приведем еще один пример точечной оценки. Пусть каждый объект генеральной совокупности характеризуется двумя количественными признаками x и y. Например, деталь может иметь два размера – длину и ширину. Можно в различных районах измерять концентрацию вредных веществ в воздухе и фиксировать количество легочных заболеваний населения в месяц. Можно через равные промежутки времени сопоставлять доходность акций данной корпорации с каким-либо индексом, характеризующим среднюю доходность всего рынка акций. В этом случае генеральная совокупность представляет собой двумерную случайную величину x, h. Эта случайная величина принимает значения x, y на множестве объектов генеральной совокупности. Не зная закона совместного распределения случайных величин x и h, мы не можем говорить о наличии или глубине корреляционной связи между ними, однако некоторые выводы можно сделать, используя выборочный метод. Выборку объема n в этом случае представим в виде таблицы, где
3.Выборочный коэффициент корреляции рассчитывается по формуле
Здесь Выборочный коэффициент корреляции можно рассматривать как точечную оценку коэффициента корреляции r x h, характеризующего генеральную совокупность. Выборочные параметры Пусть выборочный параметр d рассматривается как выборочная оценка параметра D генеральной совокупности и при этом выполняется равенство M d = D. Интервальные оценки. Точечные оценки параметров генеральной совокупности могут быть приняты в качестве ориентировочных, первоначальных результатов обработки выборочных данных. Их недостаток заключается в том, что неизвестно, с какой точностью оценивается параметр. Если для выборок большого объема точность обычно бывает достаточной (при условии несмещенности, эффективности и состоятельности оценок), то для выборок небольшого объема вопрос точности оценок становится очень важным. Введем понятие интервальной оценки неизвестного параметра генеральной совокупности (или случайной величины x, определенной на множестве объектов этой генеральной совокупности). Обозначим этот параметр через D. По сделанной выборке по определенным правилам найдем числа D 1 и D 2, так чтобы выполнялось условие: P (D 1 < D < D 2) =P (D Î (D 1; D 2)) = g Числа D 1 и D 2 называются доверительными границами, интервал (D 1, D 2) — доверительным интервалом для параметра D. Число g называется доверительной вероятностью или надежностью сделанной оценки. Сначала задается надежность. Обычно ее выбирают равной 0.95, 0.99 или 0.999. Тогда вероятность того, что интересующий нас параметр попал в интервал (D 1, D 2) достаточно высока. Число (D 1 + D 2) / 2 – середина доверительного интервала – будет давать значение параметра D с точностью (D 2 – D 1) / 2, которая представляет собой половину длины доверительного интервала. Границы D 1 и D 2 определяются из выборочных данных и являются функциями от случайных величин x 1, x 2,..., x n , а следовательно – сами случайные величины. Отсюда – доверительный интервал (D 1, D 2) тоже случаен. Он может покрывать параметр D или нет. Именно в таком смысле нужно понимать случайное событие, заключающееся в том, что доверительный интервал покрывает число D.
Тема 2.1. Выборки и их характеристики 1. Предмет и задачи математической статистики. 2. Генеральная и выборочная совокупности. 3. Статистическое распределение выборки. 4. Эмпирическая функция распределения. 5. Графическое изображение статистического распределения. 6. Числовые характеристики статистического распределения. 7. Корреляционный анализ выборочной совокупности (оценка выборочного корреляционного момента системы двух случайных величин; регрессионный анализ двух случайных величин). Математическая статистика является частью общей прикладной математической дисциплины “Теория вероятностей и математическая статистика”, однако задачи, решаемые ею, носят специфический характер. Если теория вероятностей исследует Явления, полностью заданные их моделью, то в математической статистике вероятностная модель определена с точностью до неизвестных параметров. Отсутствие сведений о параметрах компенсируется “пробными” испытаниями, на основе которых и восстанавливается недостающая информация. Цель математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов. Первой задачей математической статистики является указание методов сбора и группировки статистических сведений, которые получены в результате экспериментов или наблюдений. Вторая задача — это разработка методов анализа статистических данных: оценки неизвестных вероятности события, а также функции и параметров распределения; оценка зависимости случайной величины от других случайных величин; проверка статистических гипотез о виде и величинах параметров неизвестного распределения. Рассмотрим некоторые из этих вопросов. Выборки На практике сплошное исследование (каждого объекта из интересующей нас совокупности) проводят крайне редко. К тому же если эта совокупность содержит большое число объектов или исследование объекта требует нарушения его функционального стандарта, то сплошное исследование нереально. В таких случаях из всей совокупности случайно отбирают ограниченное число объектов и подвергают их исследованию. Введем основные понятия, связанные с выборками. Генеральной совокупностью называется совокупность объектов, из которых производится выборка. Выборочной совокупностью(выборкой) называется совокупность случайно отобранных объектов из генеральной совокупности. Число объектов в совокупности называется ее объемом. Пример 1. Пусть из 2000 изделий отобрано для обследования 100 изделий. Тогда объем генеральной совокупности N = 2000, а объем выборки п = 100. Выборку можно осуществлять двумя способами. Если после исследования объект из выборки возвращается в генеральную совокупность, то такая выборка называется повторной; если объект не возвращается в генеральную совокупность, то выборка называется бесповторной.
Выборка называется репрезентативной (представительной), если по ее данным можно достаточно уверенно судить об интересующем признаке генеральной совокупности. Способы отбора Различают два способа отбора: без расчленения генеральной совокупности на части и с расчленением. К первому относятся простые случайные отборы (либо повторный, либо бесповторный), когда объекты извлекают по одному из всей генеральной совокупности; такой отбор можно производить с использованием таблицы случайных чисел. Второй способ отбора включает следующие разновидности, соответствующие способам расчленения генеральной совокупности. Отбор, при котором объекты отбираются из каждой “типической ” части генеральной совокупности, называется типическим. Например, отбор деталей из продукции каждого станка, а не из их общего количества является типическим. Если генеральную совокупность делят на число групп, равное объему выборки, с последующим отбором из каждой группы по одному объекту, то такой отбор называется механическим. Серийным называется отбор, при котором объекты отбираются не по одному, а сериями; этот способ используется, когда исследуемый признак имеет незначительные колебания в различных сериях. На практике часто употребляется комбинирование указанных выше способов отбора. Например, генеральную совокупность разбивают на серии одинакового объема, затем случайным образом отбирают несколько серий и в завершение случайным извлечением отдельных объектов составляют выборку. Конкретная комбинация способов отбора объектов из генеральной совокупности определяется требованием репрезентативности выборки. Таким образом на выборку будем смотреть как на совокупность независимых случайных величин x 1, x 2,..., x n, распределенных так же, как и случайная величина x, представляющая генеральную совокупность. Выборочные значения x 1, x 2,..., xn – это значения, которые приняли эти случайные величины в результате 1-го, 2-го,..., n -го эксперимента.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 126; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.150.59 (0.042 с.) |

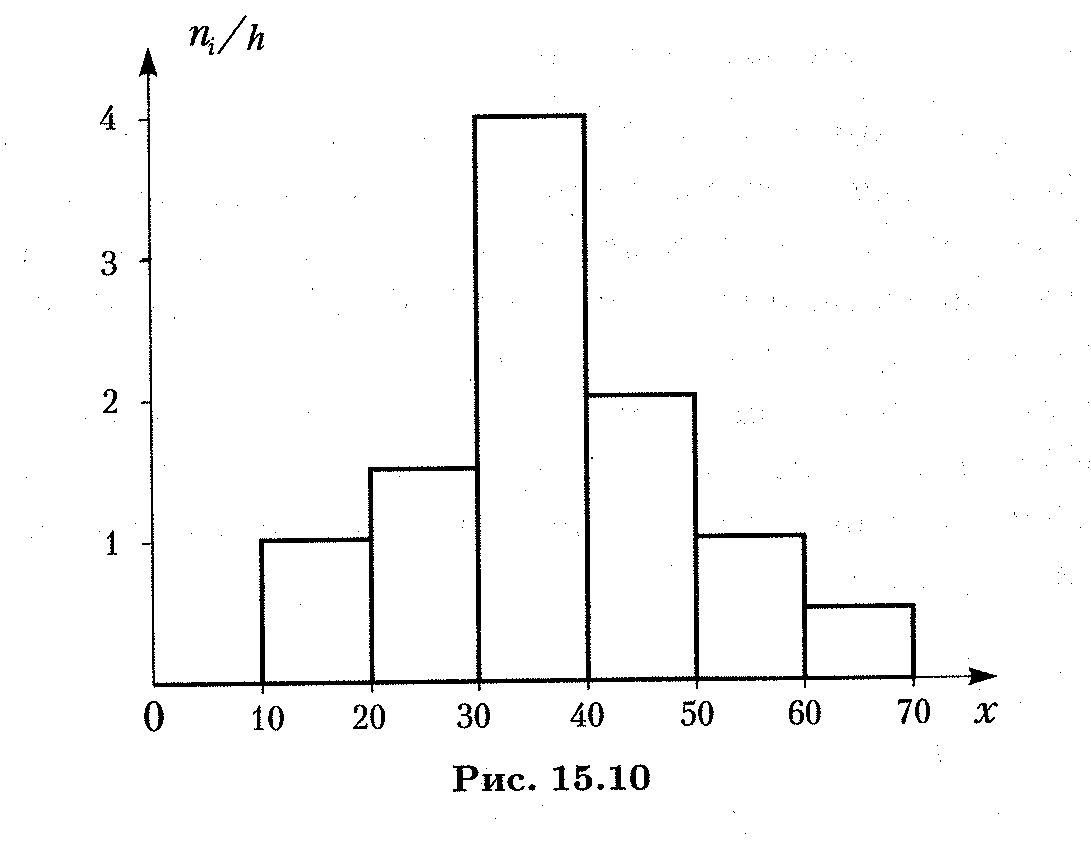 Аналогичным образом определяется и гистограмма относительных частот; в этом случае высоты прямоугольников, составляющих ступенчатую фигуру, определяются отношениями сумм относительных частот, попадающих в интервал
Аналогичным образом определяется и гистограмма относительных частот; в этом случае высоты прямоугольников, составляющих ступенчатую фигуру, определяются отношениями сумм относительных частот, попадающих в интервал 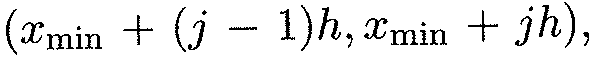 к длине интервала h, т.е. величинами Wj / h. Нетрудно видеть, что площадь гистограммы относительных частот равна единице (сумме относительных частот выборки).
к длине интервала h, т.е. величинами Wj / h. Нетрудно видеть, что площадь гистограммы относительных частот равна единице (сумме относительных частот выборки).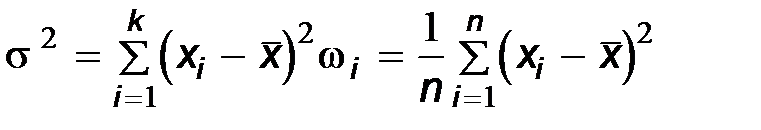
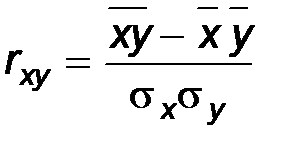
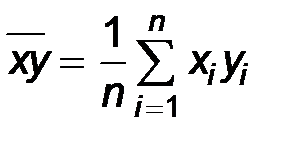 ,
, 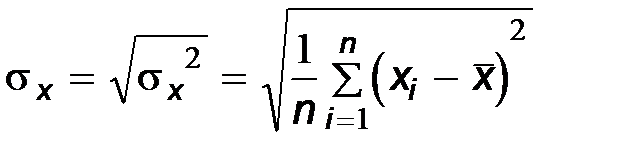 ,
,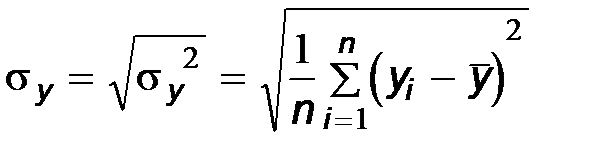 .
.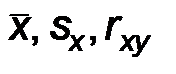 или любые другие зависят от того, какие объекты генеральной совокупности попали в выборку и различаются от выборки к выборке. Поэтому они сами являются случайными величинами.
или любые другие зависят от того, какие объекты генеральной совокупности попали в выборку и различаются от выборки к выборке. Поэтому они сами являются случайными величинами.


