
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Акустические свойства горных породСодержание книги
Поиск на нашем сайте
В первом приближении все горные породы можно считать упругими телами. Рассмотрим некоторые элементы деформаций горных пород и распространяющиеся в них упругие колебания. Если к образцу горной породы длиной l и диаметром d приложить растягивающую силу F (рис. 3.20), то он удлинится на величину ∆l, а диаметр его уменьшится на величину ∆d. Величина напряжения, действующего на единицу площади S поперечного сечения образца, будет равна
Рисунок 3.20 – Схема растяжения образца горной породы Согласно закону Гука между приложенным напряжением и возникающими деформациями должна существовать прямая пропорциональность. Следовательно, ∆l = ар, ∆ d = bp, (3.8) где а и b – коэффициенты пропорциональности.
Эти коэффициенты зависят как от свойств вещества, так и от размера образца. Чтобы коэффициенты а и b характеризовали только упругие свойства вещества, введем понятие об относительном удлинении δ l и относительном поперечном сжатии δ d: Подставив эти величины в уравнение (3.8), получим где Е – модуль продольного растяжения (коэффициент Юнга);
Упругая среда характеризуется также плотностью σ. Скорость распространения продольной упругой волны а скорость распространения поперечной упругой волны Для реальных пород Реальные горные породы не обладают достаточно совершенной связью между составляющими породу фазами (скелет породы, флюиды, заполняющие поры и трещины), поэтому скорости распространения и затухания в них упругих колебаний отличаются от идеальных условий, причем тем больше, чем менее совершенна эта связь. Акустическая жесткость среды характеризуется произведением плотности а на скорость распространения упругих волн Акустическое поле может создаваться одним, двумя или несколькими источниками излучения. Динамические и кинематические характеристики распространения упругих колебаний измеряются в одной или нескольких точках акустического поля. Распространение упругих волн является периодическим процессом. Основными характеристиками такого процесса являются: 1) период – время повторения цикла колебания; 2) амплитуда – максимальное смещение колеблющейся частицы; 3) фаза – мгновенное состояние колеблющейся частицы тела. Производные от этих величин – частота колебаний, длина волны и др. На рисунке 3.21 показано схематическое изображение акустического поля и распространения упругих колебаний. Сложное движение в любой механической колеблющейся системе может быть представлено как одновременно происходящие элементарные движения: свободные, затухающие и вынужденные колебания. Свободные колебания – это колебания, вызванные первоначальным внешним возбуждением, примером которого может быть движение маятника, натянутой резиновой нити или пружины после внешнего воздействия на них. Эти колебания с некоторыми допущениями можно рассматривать как гармонические. Затухающие колебания возникают в случае, когда в системе содержатся элементы, поглощающие, рассеивающие первоначальную энергию свободных колебаний. Если на свободные колебания воздействовать колебаниями с периодом более длительным, чем период свободных колебаний, то возникают так называемые вынужденные колебания. Упругая волна от точки к точке распространяется со скоростью, зависящей от свойств среды.
Рис. 3.21. Схематическое изображение акустического поля: а – распространение поперечных волн; б – распространение продольных волн; в – волновая картина; Т – период волны; А – ее амплитуда; φ – фаза волны; t – время; l – расстояние
Одной из важных характеристик распространения колебания является длина волны λ: где f – частота колебаний; Скорость, с которой перемещается в пространстве заданная фаза волны, называется фазовой скоростью где k – волновое число, характеризующее движение в пространстве: Разделение волн, возникающих в реальных средах, осуществляется на основании ряда признаков: взаимодействие волны со средой, показатель расхождения энергии волны по фронту распространения и др.
|
||||
|
Последнее изменение этой страницы: 2020-03-26; просмотров: 256; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.16.251 (0.006 с.) |

 . (3.7)
. (3.7)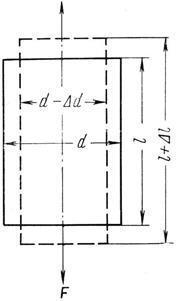
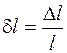 ;
; 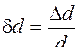 .
. ,
,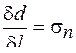 ,
, – модуль поперечного сжатия (коэффициент Пуассона).
– модуль поперечного сжатия (коэффициент Пуассона). зависит от упругих свойств среды Е,
зависит от упругих свойств среды Е,  , (3.9)
, (3.9) . (3.10)
. (3.10)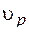 ≈ (1,4 ÷ 1,75)
≈ (1,4 ÷ 1,75) 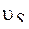 , т.е.
, т.е. 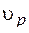 всегда больше
всегда больше  , так как продольные волны распространяются в твердых, жидких и газообразных фазах, а поперечные – преимущественно в твердых телах.
, так как продольные волны распространяются в твердых, жидких и газообразных фазах, а поперечные – преимущественно в твердых телах.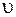 .
.
 , (3.11)
, (3.11)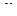 – угловая частота.
– угловая частота.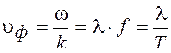 , (3.12)
, (3.12)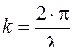 . (3.13)
. (3.13)


