
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кажущееся удельное сопротивление пластаСодержание книги
Поиск на нашем сайте
неограниченной мощности. Палетки БКЗ Результаты расчета кажущегося удельного сопротивления для пласта неограниченной мощности, выполненного Л.М. Альпиным, представлены в виде кривых, выражающих зависимость а) для непроницаемого пласта – от удельных сопротивлений пласта б) для проницаемого пласта при наличии зоны проникновения, кроме перечисленных параметров, – от удельного сопротивления зоны проникновения Эти кривые называются кривыми бокового каротажного зондирования (БКЗ). Такие кривые, сгруппированные по определенному признаку (двухслойные, трехслойные) и выражающие зависимость Двухслойные кривые БКЗ рассчитаны для условий, когда проникновение промывочной жидкости в пласт отсутствует. При этом возможны следующие случаи: а) сопротивление промывочной жидкости, заполняющей скважину, меньше сопротивления пласта ( б) сопротивление жидкости больше сопротивления пласта (
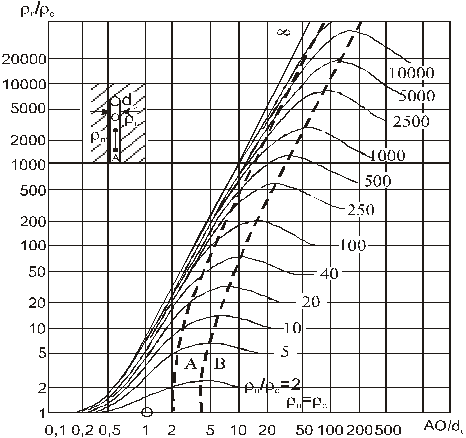
Рис. 3.6. Палетка БКЗ-1А для градиент-зондов при ρ п > ρ с (по Л.М. Альпину)
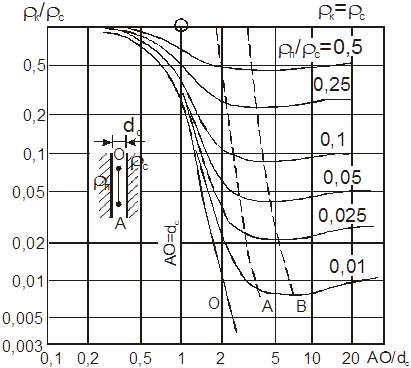
Рис. 3.7. Палетка БКЗ-1Б для градиент-зондов при ρ п < ρ с (по Л.М. Альпину) Кривые палеток БКЗ-1 в своей правой части асимптотически приближаются к значениям удельного сопротивления пласта. Изображенная на палетках кривая А характеризует геометрическое место точек пересечения кривых БКЗ с их правыми асимптотами, кривая В – геометрическое место точек (максимумов и минимумов) кривых. Двухслойные кривые БКЗ обозначают одним относительным параметром Трехслойные кривые БКЗ рассчитаны для случая проникновения промывочной жидкости в пласт. При этом в примыкающей к скважине части пласта образуется зона проникновения (ЗП), условно принимаемая за цилиндрическую, диаметром D и удельным сопротивлением Трехслойные кривые БКЗ определяются пятью параметрами При проникновении фильтра промывочной жидкости в пласт возможны два случая: снижение удельного сопротивления (понижающее проникновение) и, наоборот, увеличение его сопротивления (повышающее проникновение). Принадлежность кривой БКЗ к повышающему либо понижающему проникновению промывочной жидкости определяется величиной
Рис. 3.8. Палетка БКЗ-4/20 для градиент-зондов (по Л.М. Альпину) Каждая кривая на трехслойной палетке БКЗ изображает зависимость Например, палетка БКЗ с шифром 4/20 означает, что на ней представлен набор кривых зависимости Литологически такие пласты могут быть представлены проницаемыми нефтегазоносными породами. Кроме того, подобный тип кривых наблюдается для проницаемых и водоносных пластов, если удельное сопротивление фильтрата бурового раствора меньше удельного сопротивления пластовой воды. Интерпретацию кривых при неглубоком проникновении бурового раствора обычно производят с помощью трехслойных палеток.
|
||||
|
Последнее изменение этой страницы: 2020-03-26; просмотров: 192; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.54.190 (0.007 с.) |

 от различных определяющих его параметров:
от различных определяющих его параметров: и промывочной жидкости
и промывочной жидкости 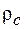 , диаметра скважины
, диаметра скважины  и длины зонда
и длины зонда 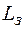 ;
; и ее диаметра D.
и ее диаметра D.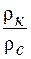 от
от 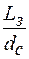 для пласта неограниченной мощности, называются палетками БКЗ. Различают кривые БКЗ двух основных типов – двухслойные и трехслойные.
для пласта неограниченной мощности, называются палетками БКЗ. Различают кривые БКЗ двух основных типов – двухслойные и трехслойные. <
<  >
>  ). Двухслойные расчетные кривые БКЗ сгруппированы в палетки, обозначаемые БКЗ-1А (при
). Двухслойные расчетные кривые БКЗ сгруппированы в палетки, обозначаемые БКЗ-1А (при  <
< 
 , который называется модулем кривой БКЗ.
, который называется модулем кривой БКЗ. с промежуточным значением между pс и неизмененной части пласта
с промежуточным значением между pс и неизмененной части пласта 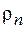 .
. ,
,  и
и  . Если
. Если  < 1, то наблюдается повышающее проникновение, при
< 1, то наблюдается повышающее проникновение, при  > 1 – понижающее. Обычно на одну и ту же палетку наносят кривые, соответствующие повышающему и понижающему проникновению фильтрата промывочной жидкости (рис. 3.8).
> 1 – понижающее. Обычно на одну и ту же палетку наносят кривые, соответствующие повышающему и понижающему проникновению фильтрата промывочной жидкости (рис. 3.8).
 от относительного размера зонда
от относительного размера зонда  ,
, 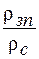 и
и  , из которых первые два отражают шифр палетки, а третий – шифр кривой.
, из которых первые два отражают шифр палетки, а третий – шифр кривой.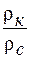 от
от 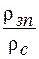 = 20 (рис. 3.8). При повышающем проникновении фильтрата промывочной жидкости в пласт удовлетворяется условие
= 20 (рис. 3.8). При повышающем проникновении фильтрата промывочной жидкости в пласт удовлетворяется условие 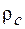 < <
< <  , при понижающем
, при понижающем  <
< 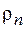 .
.


