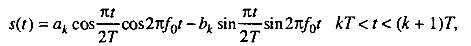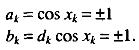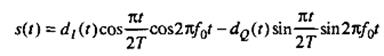Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Манипуляция с минимальным сдвигомСодержание книги Поиск на нашем сайте
Главное преимущество OQРSК перед QРSК (устранение внеполосной интерференции) наводит на мысль, что можно дополнительно усилить формат OQРSК, устранив разрывные переходы фазы. Это стало мотивацией разработки схем модуляции без разрыва фазы. Одной из таких схем является манипуляция с минимальным сдвигом (МSК). МSК можно рассматривать как частный случай частотной манипуляции без разрыва фазы (СРРFК) или как частный случай OQРSК с синусоидальным взвешиванием символов. В первом случае сигнал МSК можно представить следующим образом
(1)
Уравнение (1) можно переписать в квадратурном представлении
(2)
Где
Синфазный компонент обозначается как akcos(πt/2T)cos2πf0t, где cos2πf0t ‑ несущая, cos(πt/2T) ‑ синусоидальное взвешивание символов, ak‑ информационно-зависимый член. Подобным образом квадратурный компонент ‑ это bksin(πt/2T)sin2πf0t, ‑ sin2πf0t квадратурное слагаемое несущей, sin(πt/2T) ‑ такое же синусоидальное взвешивание символов, bk — информационно-зависимый член. Из-за требования непрерывности фазы величина ak может измениться лишь при переходе функции cos(πt/2T) через нуль, bk а только при переходе через нуль sin(πt/2T). Следовательно, взвешивание символов в синфазном или квадратурном канале ‑ это синусоидальный импульс с периодом 2Т и переменным знаком. Как и в случае ОQРSК, синфазный и квадратурный компоненты сдвинуты относительно друг друга на Т секунд.
Отметим, что xk в уравнении (1) ‑ это функция разности между прежним и текущим информационными битами (дифференциальное кодирование). Таким образом, величины ak и bk в уравнении можно рассматривать как дифференциально кодированные компоненты исходных данных dk. Чтобы биты данных были независимы между собой, знаки последовательных импульсов квадратурного и синфазного каналов от одного импульсного интервала, длительностью 2Т секунд, до следующего должны быть случайными импульсами. Таким образом, если уравнение (2) рассматривать как частный случай модуляции OQPSK, его можно переписать в недифференциальной форме
(3)
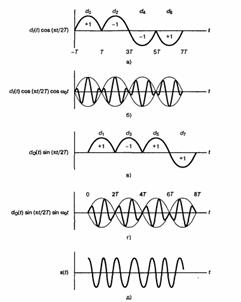
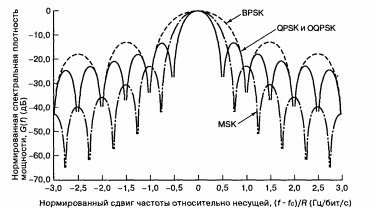
Схема МSК, записанная в этой форме, иногда называется МSК с предварительным кодированием. Графическое представление уравнения (3) дано на рис. 8. На рис. 8, а и в показано синусоидальное взвешивание импульсов синфазного и квадратурного каналов. Эти последовательности представляют собой те же информационные последовательности, что и на рис. 6, но здесь умножение на синусоиду дает более плавные переходы фазы, чем в исходном представлении данных. На рис. 8, б и г показана модуляция ортогональных компонентов cos2πf0t и sin2πf0t синусоидальными потоками данных. На рис. 8, д представлено суммирование ортогональных компонентов, изображенных на рис. 8, б и г. Итак, из уравнения (3) и рис. 8 можно заключить следующее: 1) сигнал s(t) имеет постоянную огибающую; 2) фаза радиочастотной несущей непрерывна при битовых переходах; 3) сигнал s(t) можно рассматривать как РSК-модулированный сигнал с частотами передачи f0+1/4Т и f0-1/4Т. Таким образом, минимальное разнесение тонов, требуемое при модуляции МSК, 1/2T, что равно половине скорости передачи битов. Разнесение тонов, требуемое для МSК,‑ это половина (1/T) разнесения, необходимого при некогерентном детектировании FSК-модулированных сигналов. Это объясняется тем, что фаза несущей известна и непрерывна, что позволяет осуществить когерентную демодуляцию сигнала. Нормированная спектральная плотность мощности (Р=1Вт) для QРSК, OQPSК и МSК изображена на рис. 8. Для сравнения здесь же приводится спектральный график ВРSК. Не должно удивлять, что ВРSК требует большей полосы пропускания, чем другие типы модуляции, при том же уровне спектральной плотности. Теоретическая эффективность использования полосы частот схемы ВРSК вдвое меньше, чем схемы QРSК. Из рис. 9 видно, что боковые максимумы графика МSК ниже, чем графика QРSК или ОQРSК. Это является следствием умножения потока данных на синусоиду и дает большое количество плавных фазовых переходов. Чем плавнее переход, тем быстрее спектральные хвосты стремятся к нулю. Модуляция МSК спектрально эффективнее QРSК или OQРSК; тем не менее, как видно из рис. 9, спектр МSК имеет более широкий основной максимум, чем спектр QРSК или OQРSК. Следовательно, МSК нельзя назвать удачным выбором при наличии узкополосных линий связи. В то же время МSК стоит использовать в системах с несколькими несущими, поскольку ее относительно малые побочные максимумы спектра позволяют избежать значительных помех соседних каналов. То, что спектр QРSК имеет более узкий основной максимум, чем МSК, объясняется тем, что при данной скорости передачи битов скорость передачи символов QРSК вдвое меньше скорости передачи символов МSК
Рис. 9. Нормированная спектральная плотность мощности для ВРSК, QРSК, OQРSК и МSК.
|
||||||
|
Последнее изменение этой страницы: 2020-03-02; просмотров: 178; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.69.138 (0.009 с.) |

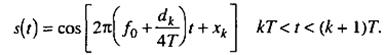
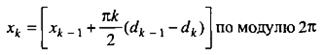 Здесь f0 ‑ несущая частота,dk=±1 представляет биполярные данные, которые передаются со скоростью R=1/T, а xk — это фазовая постоянная для k-го интервала передачи двоичных данных. При dk =1 передаваемая частота ‑ это f0+1/4Т, а при dk=-1 ‑ это f0-1/4Т. Следовательно, разнесение тонов в МSК составляет половину от используемого при ортогональной FSК с некогерентной демодуляцией, откуда и название — манипуляция с минимальным сдвигом. В течение каждого T-секундного интервала передачи данных значение xk постоянно, т.е. xk=0 или π, что диктуется требованием непрерывности фазы сигнала в моменты t=kТ, Это требование накладывает ограничение на фазу, которое можно представить следующим рекурсивным соотношением для xk
Здесь f0 ‑ несущая частота,dk=±1 представляет биполярные данные, которые передаются со скоростью R=1/T, а xk — это фазовая постоянная для k-го интервала передачи двоичных данных. При dk =1 передаваемая частота ‑ это f0+1/4Т, а при dk=-1 ‑ это f0-1/4Т. Следовательно, разнесение тонов в МSК составляет половину от используемого при ортогональной FSК с некогерентной демодуляцией, откуда и название — манипуляция с минимальным сдвигом. В течение каждого T-секундного интервала передачи данных значение xk постоянно, т.е. xk=0 или π, что диктуется требованием непрерывности фазы сигнала в моменты t=kТ, Это требование накладывает ограничение на фазу, которое можно представить следующим рекурсивным соотношением для xk